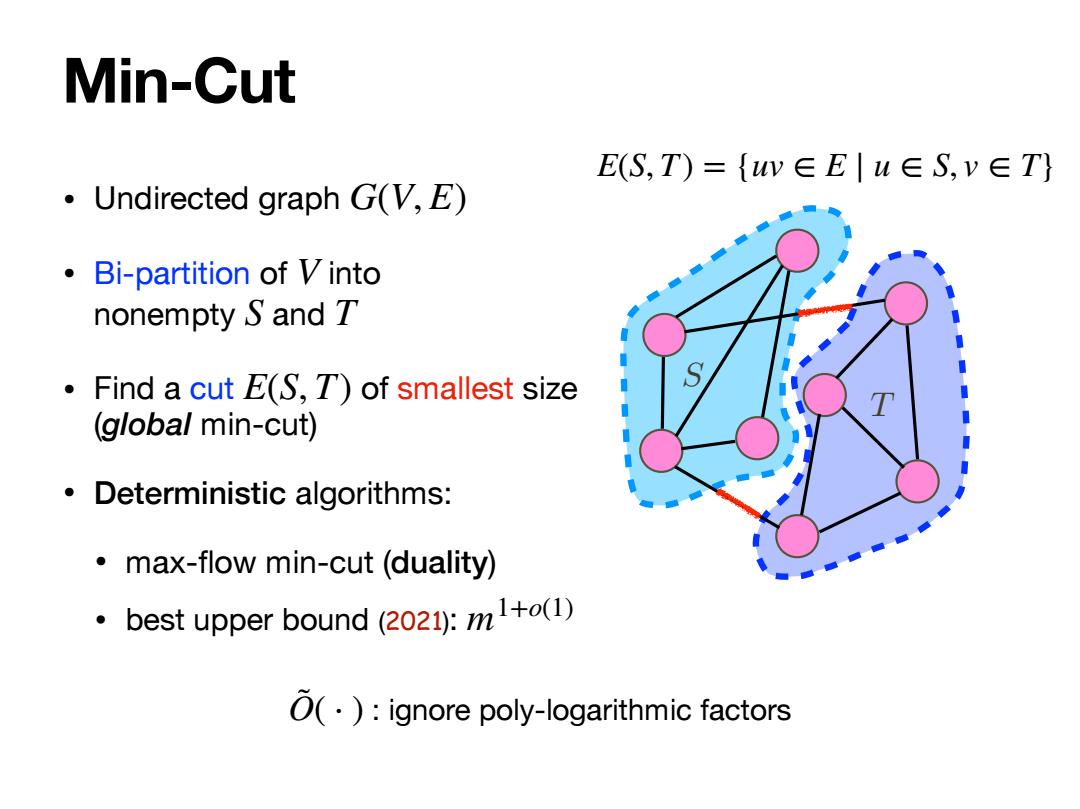
Min-Cut E(S,T)={uw∈E|u∈S,v∈T} Undirected graph G(V,E) Bi-partition of Vinto nonempty S and T Find a cut E(S,T)of smallest size (global min-cut) Deterministic algorithms: max-flow min-cut(duality) best upper bound (2021):m1+(1) O(.):ignore poly-logarithmic factors
Min-Cut • Undirected graph • Bi-partition of into nonempty and • Find a cut of smallest size (global min-cut) • Deterministic algorithms: • max-flow min-cut (duality) • best upper bound (2021): G(V, E) V S T E(S, T) m1+o(1) T S E(S, T) = {uv ∈ E ∣ u ∈ S, v ∈ T} : ignore poly-logarithmic factors O˜( ⋅ )

Min-Cut E(S,T)={uw∈E|u∈S,v∈T} Undirected graph G(V,E) ·Too many cuts: there are 29()bi-partitions ·(will see later)only at most O(n)min-cuts Generate a random cut that is a min-cut with large enough probability?
Min-Cut • Undirected graph • Too many cuts: • there are bi-partitions • (will see later) only at most min-cuts • Generate a random cut that is a min-cut with large enough probability? G(V, E) 2Ω(n) O(n2 ) T S E(S, T) = {uv ∈ E ∣ u ∈ S, v ∈ T}

Contraction Undirected multigraph GV,E) ·multigraph: ·allow parallel edges ·but no self-loop contract(e):e uv is an edge merges two endpoints u and v
Contraction • Undirected multigraph • multigraph: • allow parallel edges • but no self-loop • contract( ): is an edge • merges two endpoints and G(V, E) e e = uv u v e
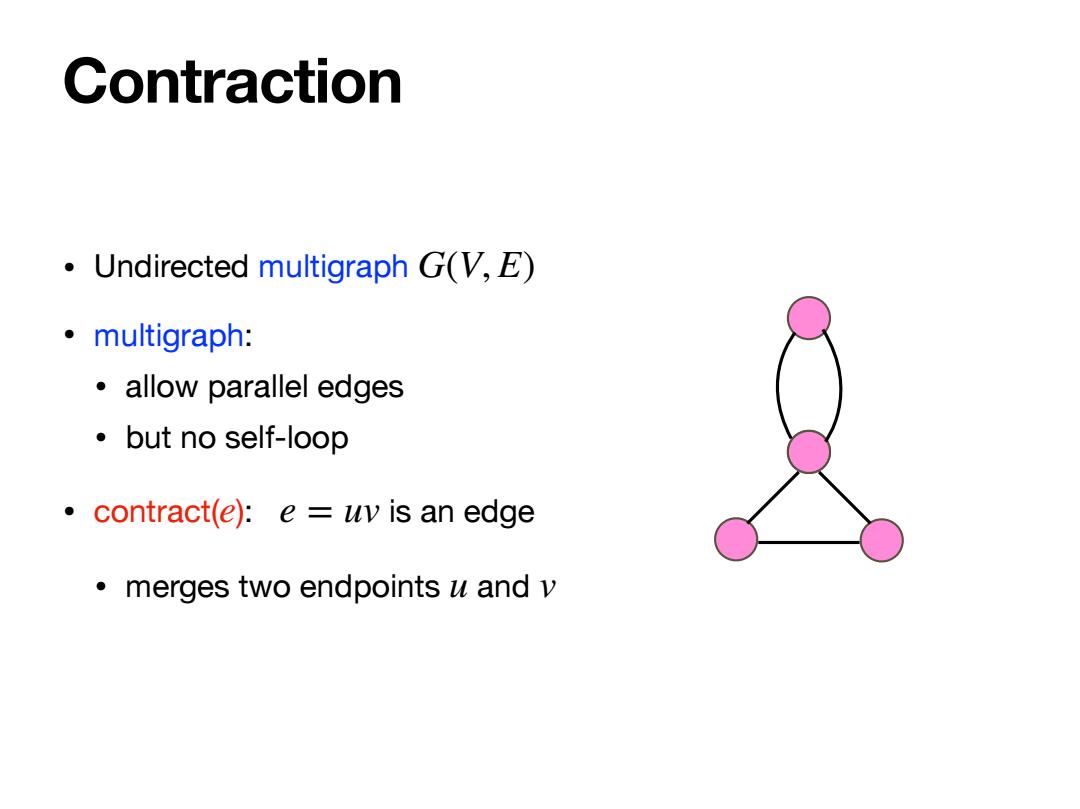
Contraction Undirected multigraph GV,E) 。multigraph: ·allow parallel edges ·but no self-loop contract(e):e uv is an edge merges two endpoints u and v
Contraction • Undirected multigraph • multigraph: • allow parallel edges • but no self-loop • contract( ): is an edge • merges two endpoints and G(V, E) e e = uv u v

Karger's Min-Cut Algorithm ·multigraph G(V,E) Karger's Algorithm: whileV>2 do: pick random e∈E; contract(e); return remaining edges; random:uniformly and independently at random
Karger’s Algorithm: while do: pick random ; contract ; return remaining edges; |V| > 2 e ∈ E (e) • multigraph G(V, E) Karger’s Min-Cut Algorithm random: uniformly and independently at random