
二、频域的有限化和离散化 与时域一样,对频域也要进行有限化和离散化处理。 频域的有限化,是在频域轴上取一个周期的频率区 间?=9,。频域的离散化,就是对一个周期内的频 谱进行抽样,[0,2]有(k=01,2,N-1),则 9,=g-2π17=2r-2r -N-NT-T (5-5)

二、频域的有限化和离散化 需要指出,上式中,T代表信号截断的时间长度, 不是信号周期概念,因为原信号是非周期信号; 也不恩基频的概念,而是频谱离散化后相邻离散 点的频率间隔。因此为了与周期信号离散谱的符 号X,(n@)相区别,用X,(k2)来表示非周期信号频 谱离散化后的频谱。其结果分别如图5-4和式(5 6)所示
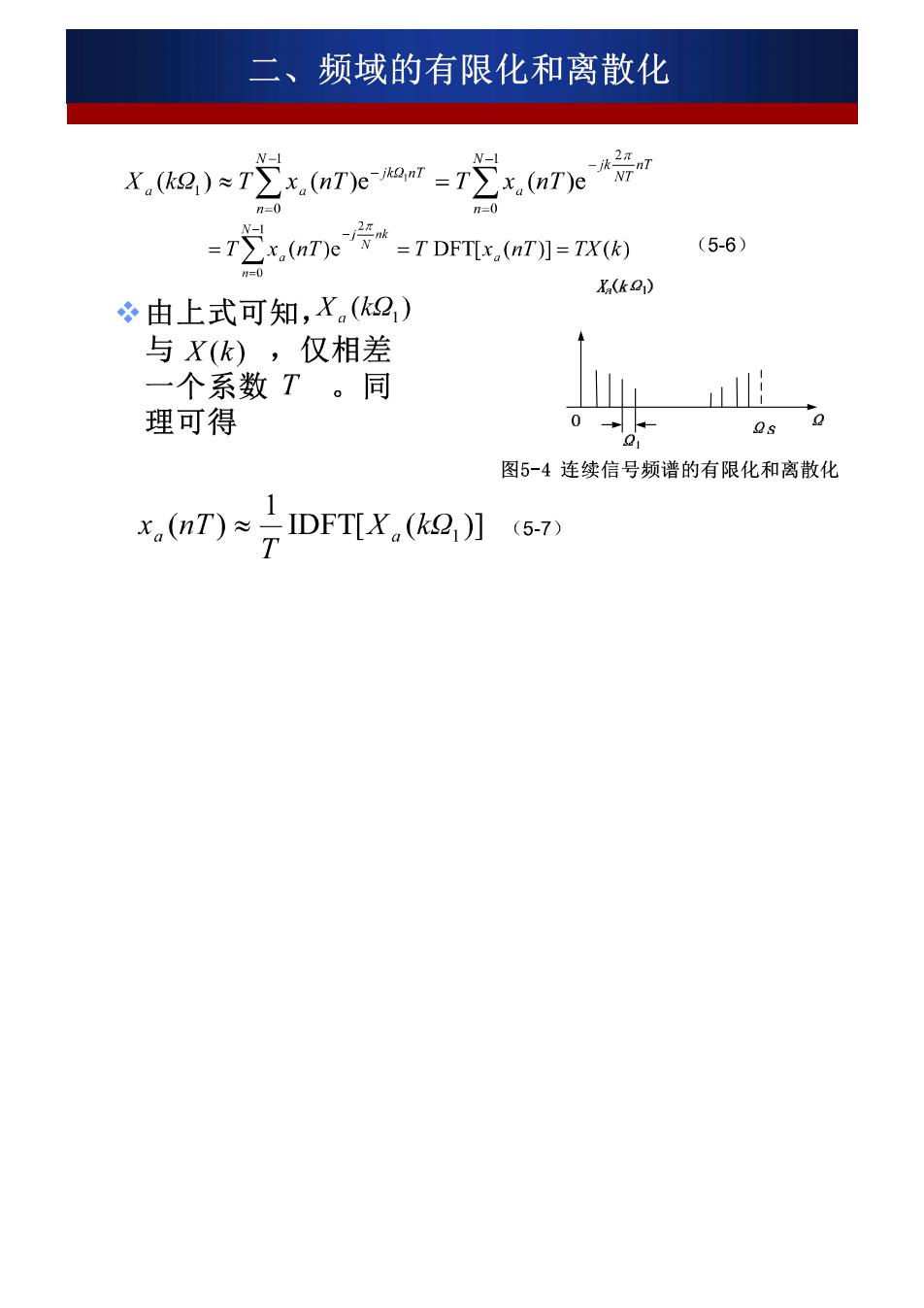
二、频域的有限化和离散化 X.a)r2 (nT)=72天aTe号 Er心ane=TDFT.(n)]=-7r (5-6) X(k) 由上式可知,X(k2) 与X(k),仅相差 一个系数T。同 理可得 0 00 图5-4连续信号频谱的有限化和离散化 x,nT)≈21DFT[X,(k2,】(57 T

二、频域的有限化和离散化 有了式(5-6)和式(5-7),就可将对连续信号 的谱分析用的谱分析来逼近,从而采用FFT算法。 同时需要说明的是,对某一信号分析时,由于关 心的是信号的结构成分,所以只需确定信号中频 率的相对量即可,因此频谱计算可以直接采用DFT 式(5-6)就是对非周期连续信号进行数字谱分析 的基本原理

三、误差产生原因及解决办法 对连续非周期信号的数字谱分析实质上是 用有限长抽样序列的DFT(离散谱)来近似 无限长连续信号的频谱(连续谱),其结 果必然会产生误差,主要的误差包括:栅 栏效应、混叠效应和频谱泄漏三种