
第五章离散傅里叶变换的应用 5.1 用DFT逼近连续时间信号的频谱 5.2 用FFT计算线卷积和相关运算 5.3 倒频谱分析 5.4 系统频谱响应函数分析及确定

内容提要 冬 离散傅里叶变换(DFT)及其快速算法(FFT)的 重要性不仅在于理论上的严格性,而且还在于工 程上的实用性,凡是可以利用傅里叶变换进行分 析、综合和处理的技术问题,都能利用FFT有效地 解决。本章将详细介绍和分析利用DFT逼近傅里叶 变换时存在的问题和解决的方法,如何利用DFT实 现快速卷积及相关运算,倒频谱的基本概念及应 用等内容
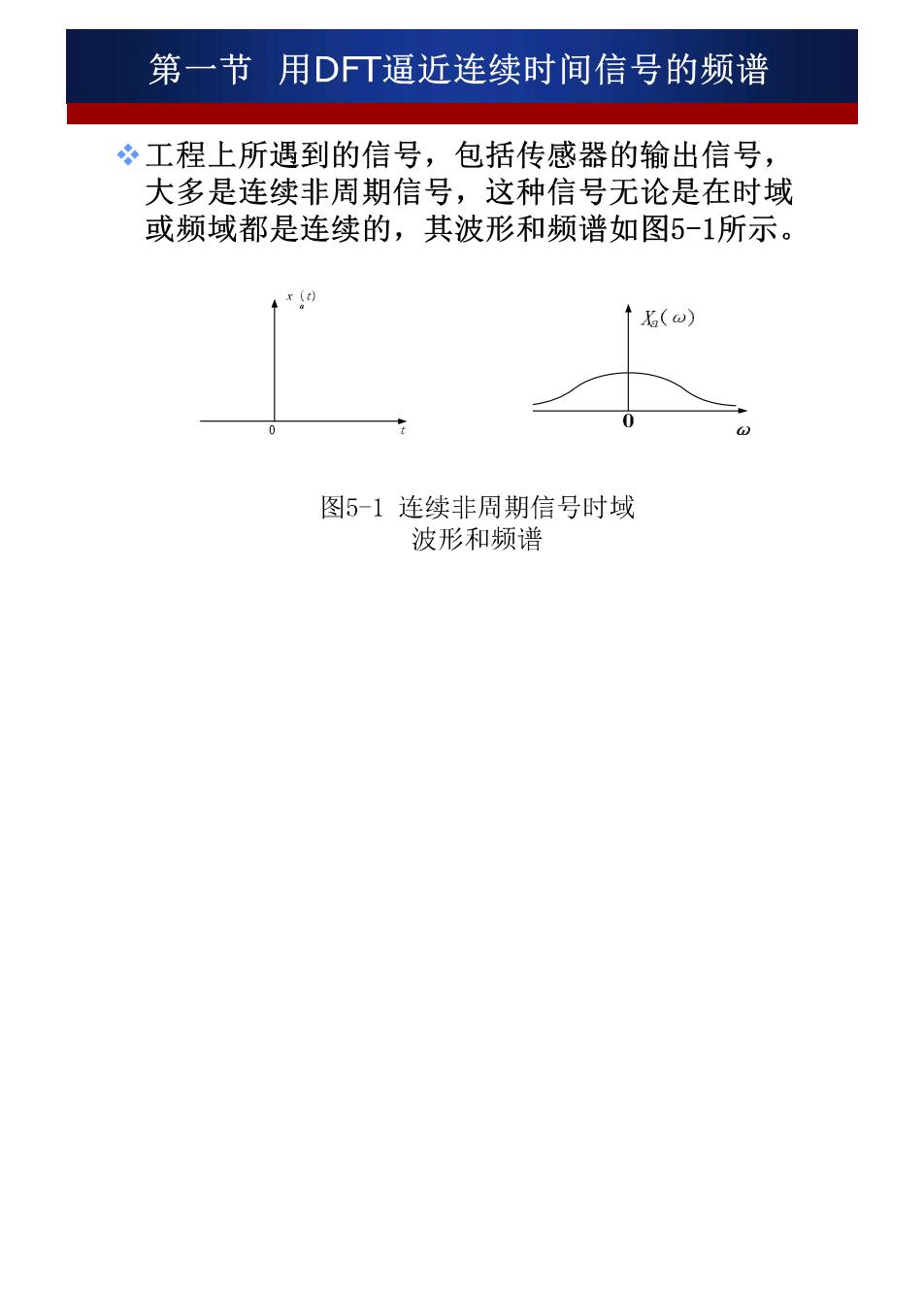
第一节用DFT逼近连续时间信号的频谱 工程上所遇到的信号,包括传感器的输出信号, 大多是连续非周期信号,这种信号无论是在时域 或频域都是连续的,其波形和频谱如图5-1所示。 图5-1连续非周期信号时域 波形和频谱

X.(o)=["x(t)e-di (5-1) x(=- X.(o)e“do (5-2) 2πJ-。 由式(5-1)、式(5-2)和图5-1,可以看 出 1)两式中的积分区间均为(一∞,∞); 2)X,()和x()都是连续函数

显然,上述两点无法满足计算机进行数字 信号处理的要求,若要应用FFT进行分析和 处理,必须在时、频域进行有限化和离散 化处理。有限化和离散化处理是在时、频 域对被处理的连续信号近似或逼近,是一 种近似处理