
2氧化层的隧穿电流的影响 对于MOS结构,当栅氧化层比较薄时,会由于氧 化层中电场的增强引起较为明显的隧穿电流。穿 越MOS晶体管栅氧化层的隧穿电流会对器件的性 能带来影响。如使电路静态功耗加大。隧穿电流 还会影响MOS器件特性和可靠性。 对MOS结构.当栅氧化层厚度大于6nm时,主要是 F一N(Fowler-.Nordheim)隧穿电流。这种情况下, 电子穿越氧化层的隧穿势垒是三角形势垒.如图 2.3(a)所示。若栅氧化层很薄,则主要是直接隧穿 电流,这种情况下,氧化层上的压降比S一SO 的势垒高度小,隧穿势垒是梯形势垒,如图2.3b) 所示
• 对于MOS结构,当栅氧化层比较薄时,会由于氧 化层中电场的增强引起较为明显的隧穿电流。穿 越MOS晶体管栅氧化层的隧穿电流会对器件的性 能带来影响。如使电路静态功耗加大。隧穿电流 还会影响MOS器件特性和可靠性。 • 对MOS结构.当栅氧化层厚度大于6nm时,主要是 F一N(Fowler-Nordheim)隧穿电流。这种情况下, 电子穿越氧化层的隧穿势垒是三角形势垒.如图 2.3(a)所示。若栅氧化层很薄,则主要是直接隧穿 电流,这种情况下,氧化层上的压降比Si一SiO2 的势垒高度小,隧穿势垒是梯形势垒,如图2.3(b) 所示
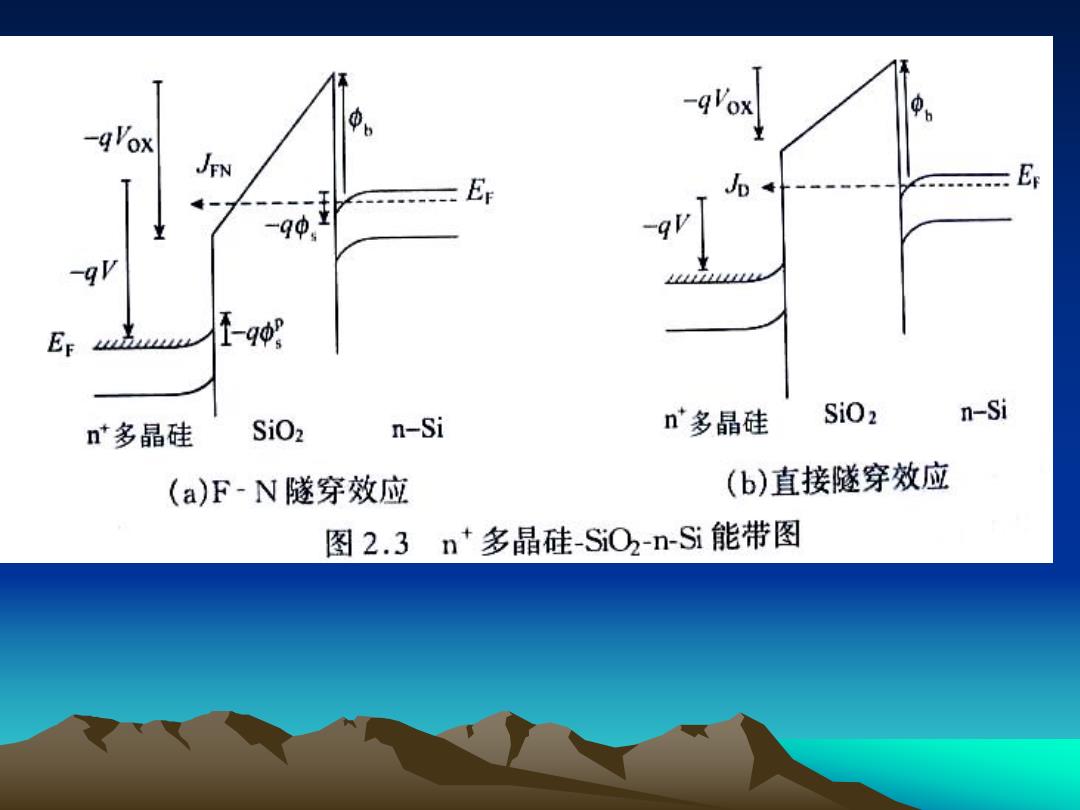
-qVox -qVox Er -9 SiO2 n-Si n多晶硅 SiOz n-Si n多晶硅 (a)F-N隧穿效应 (b)直接隧穿效应 图2.3n+多晶硅-SiO2-n-Si能带图

隧穿电流的最大特点是随氧化层中的电场强度 Eo指数增大。F一N隧穿电流密度可表示为 Jw=A·Fox exp(-B/Eox) 直接隧穿电流密度可近似表示为 A.Eox B42-(-ox)2 exp 1- +'oz 1/2 Eox
• 隧穿电流的最大特点是随氧化层中的电场强度 EOX指数增大。F一N隧穿电流密度可表示为 • 直接隧穿电流密度可近似表示为

其中,Eox是氧化层中的电 场强度,φb是Si一SiO,势 103 ◇ 数据 103 直接隧穿模型 垒高度,V是氧化层上的 18 F-N隧穿模型 电压,A、B是依赖于电子 2.5nm 有效质量、Si一SiO,势垒 高度等因素的系数, 7.6nm A≈1.25×10-6A/V2, B≈233.5MV/cm。对于很 薄的氧化层,氧化层上的 000 压降小于3.2V,这时直接 6 10 隧穿电流变得显著。 VGNV 图2.4 直接隧穿电流和F-N隧穿电流
• 其中,EOX是氧化层中的电 场强度,φb是Si—SiO2势 垒高度,Vox是氧化层上的 电压,A、B是依赖于电子 有效质量、Si一SiO2势垒 高度等因素的系数, A≈1.25×10 -6A/V2, B≈233.5MV/cm。对于很 薄的氧化层,氧化层上的 压降小于3.2V,这时直接 隧穿电流变得显著
·3、栅氧化层直接隧穿电流的计算 应用顺序隧穿理论和巴丁传输哈密 H 顿方法,把电子的直接隧穿结构分 解为如图两个子系统,其中势阱H1 为三角势阱,H2为半无限宽势阱。 入射电子态平是子系统哈密顿H, 的本征态 H平1=E, 其中H的势函数V(x)如图c)所示 H x<0 (x)= eFX, x>0 & H的势函数V2x)如图b)所示 0, V(x)= x<-1ox Vo> x>-fox b)
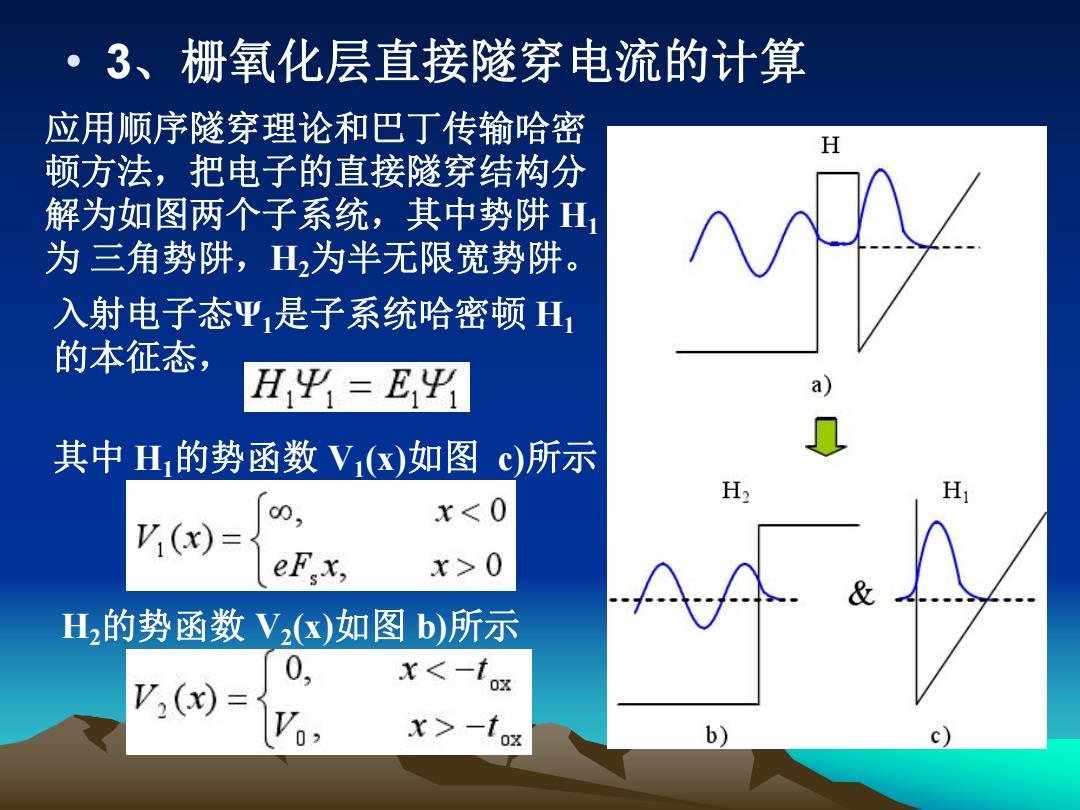
• 3、栅氧化层直接隧穿电流的计算 应用顺序隧穿理论和巴丁传输哈密 顿方法,把电子的直接隧穿结构分 解为如图两个子系统,其中势阱 H1 为 三角势阱,H2为半无限宽势阱。 入射电子态Ψ1是子系统哈密顿 H1 的本征态, 其中 H1的势函数 V1(x)如图 c)所示 H2的势函数 V2(x)如图 b)所示