>引言 f:(XoXo)= 函数沿轴方向的变化率 J0 f,(x,)= 函数沿轴方向的变化率 偏导数 函数沿坐标轴方向的变化率 函数沿任一方向的变化率?一方向导数 例如: 大气温度 在气象学中,需要确定 气压 沿某些方向的变化率
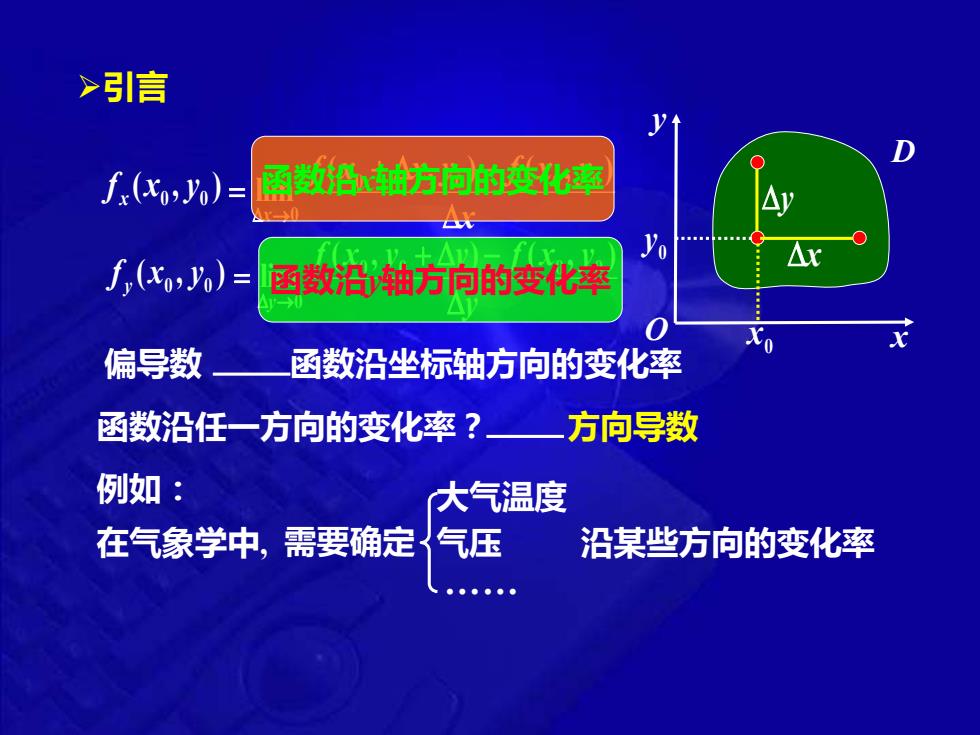
➢引言 偏导数 ( , ) 0 0 f x y x x f x x y f x y x + − = → ( , ) ( , ) lim 0 0 0 0 0 x y O D 0 x 0 y x 函数沿x轴方向的变化率 ( , ) 0 0 f x y y y f x y y f x y y + − = → ( , ) ( , ) lim 0 0 0 0 0 y 函数沿y轴方向的变化率 函数沿坐标轴方向的变化率 函数沿任一方向的变化率? 例如: 在气象学中, 需要确定 大气温度 气压 . 沿某些方向的变化率 方向导数

>引言 设u=f化,在PKJo,的某一邻域内有定义, 是以P,(x,J为起点的一条射线 =(Cosa,c0sB,c0sy)P(x,y,)是1上任点, PP=t(t≥0,PP∥→PP=店 x-x=y二h=名-=i cosa cosβcosy 射线1的参数方程: 〔x=x+tc0sa y=o+tcos B t≥0→P(x+tc0sa,y+tc0sB,z+tc0sY) =+tcosy
➢引言 设 在 ( , , ) 0 0 0 0 u = f (x, y,z) P x y z 的某一邻域内有定义, 是以 ( , , ) 0 0 0 0 l P x y z 为起点的一条射线 ) l P(x, y,z 是 上任一点, P0 P l e = (cos,cos ,cos ) l e l P P = te 0 | | ( 0), P0 P = t t t x x y y z z = − = − = − cos cos cos 0 0 0 射线 l 的参数方程: x = x0 + t cos y = y0 + t cos cos 0 z = z + t t 0 ( cos , cos , cos ) 0 0 0 P x + t y + t z + t P0 P l y x z O t

>定义 设u=f,J,2在P,(K,Jo的某一邻域U(,)内有定义,1是以 P(化o,Jyo,z为始点的一条射线,P(。+tc0sa,yn+tc0s阝,+tc0sY) 是I上另一点,且P∈U(P,),如果函数增量 f(x+tcosa,y+tcosB,to+tcosy)-f(xo>Vo,Zo) 与P到P的距离PP,=t的比值 f(x+tcosa,o+tcosB,to+tcosy)-f(xoYoZo) t 当P沿着趋于P,即1→0)时的极限存在,则称此极限为 函数f化,在P沿方向的方向导数,记作2I Ol (xo,%o,z0)
➢定义 设 在 ( , , ) 0 0 0 0 u = f (x, y,z) P x y z 的某一邻域 ( , , ) 0 0 0 0 P x y z 为始点的一条射线, 是 l 上另一点, ( cos , cos , cos ) 0 0 0 P x + t y + t z + t U(P0 ) 内有定义, l 是以 ( ), 且 P U P0 如果函数增量 ( cos , cos , cos ) ( , , ) 0 0 0 0 0 0 f x + t y + t z + t − f x y z 与 P 到 P0 的距离 | PP |= t 0 的比值 t f (x t cos , y t cos ,z t cos ) f (x , y ,z ) 0 + 0 + 0 + − 0 0 0 当 P 沿着l趋于 P0 (即 → + t 0 )时的极限存在,则称此极限为 函数 f (x, y,z) 在 P0 沿方向l的方向导数,记作 . ( , , ) 0 0 0 l x y z f

●注()二元函数f(x,y在P(x,沿方向方向角为a,) 的方向导数为 of lim f(xo+tcosa,yo+tcosB)-f(xo,yo) a1 (xo,yo) 1-→0 (2) of 刻画了函数f(x,J》,)在(化,yo,) (X0,0,z) 沿方向的变化率 lim f(x+tcosa,yo+tcos B,to+tcosy)-f(xo,yo,zo OI (xo2Yo,zo) t-→0t
t f x t y t z t f x y z t ( cos , cos , cos ) ( , , ) lim 0 0 0 0 0 0 0 + + + − = → + ( , , ) 0 0 0 l x y z f ⚫注 二元函数 f (x, y) 在 ( , ) 0 0 0 P x y 沿方向l(方向角为 , ) 的方向导数为 t f x t y t f x y t ( cos , cos ) ( , ) lim 0 0 0 0 0 + + − = → + ( , ) 0 0 l x y f (1) (2) ( , , ) 0 0 0 l x y z f 刻画了函数 f (x, y,z) 在 ( , , ) 0 0 0 0 P x y z 沿方向l的变化率

单侧极限 ●注(3)定义式的特点 比式∫分子:射线上两点函数值之差 分母:射线1上两点的距离 (4)偏导数与方向导数 例 =i of =f(x) f(x,%)存在 al (xoy) lG=-i→0/ (,)-.(6) n-g-新o =1但f(0,0)不存在 lim f(xo+tcosa,yo+tcosB,to+tcosy)-f(xo>Yo,Zo) OI (xo,yo,Zo) -0
t f x t y t z t f x y z t ( cos , cos , cos ) ( , , ) lim 0 0 0 0 0 0 0 + + + − = → + ( , , ) 0 0 0 l x y z f ⚫注 (3) (4) ( , ) ( , ) 0 0 0 0 f x y l x y f = x 单侧极限 例 定义式的特点 比式 分子: 射线l上两点函数值之差 分母: 射线l上两点的距离 偏导数与方向导数 ( , ) 0 0 f x y x 存在, e i l = e i l = − ( , ) ( , ) 0 0 0 0 f x y l x y f = − x 2 2 f (x, y) = x + y e i l = 1 (0,0) = l f (0,0) x 但 f 不存在