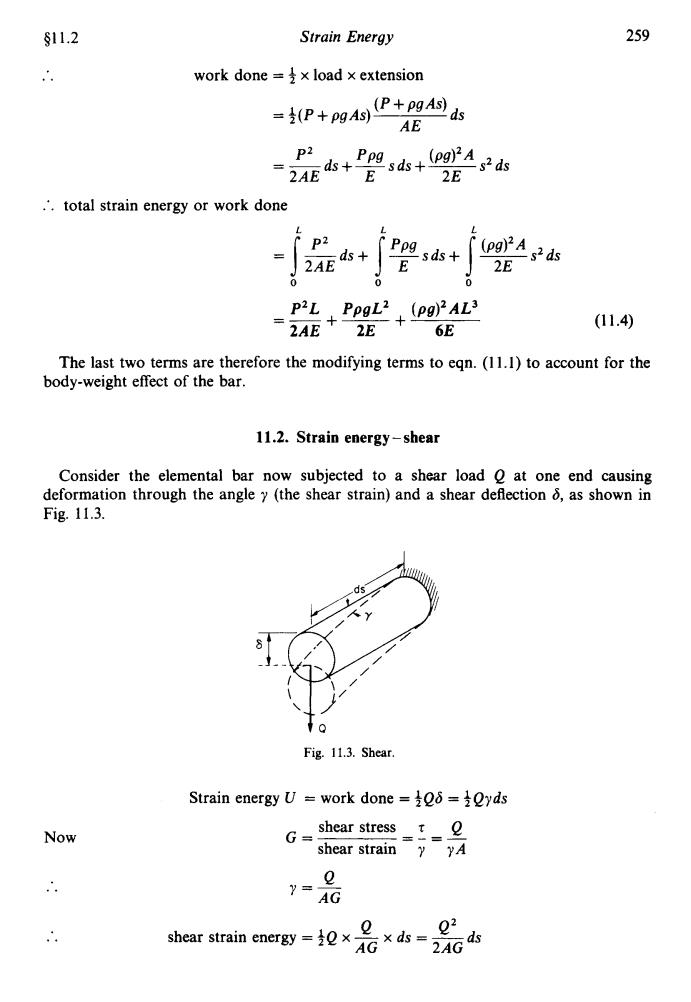
S11.2 Strain Energy 259 work done =x load x extension =5P+pgA的P+pgAd AE P2 2AEdsE = 2E .∴,total strain energy or work done P2 ds+ P sds+ 2AE E 片(p9PAg2as 2E 0 0 P2L PpgL2 (pg)2AL 2AE 2E+ 6E (11.4) The last two terms are therefore the modifying terms to eqn.(11.1)to account for the body-weight effect of the bar. 11.2.Strain energy-shear Consider the elemental bar now subjected to a shear load o at one end causing deformation through the angle y(the shear strain)and a shear deflection as shown in Fg.11.3. ds Fig.11.3.Shear. Strain energy U work done =108=Qyds Now G- shear stress t shear strain y yA y= AG Q2 shear strain energy =x Gx ds =ds
$1 1.2 Strain Energy 259 .. work done = 3 x load x extension :. total strain energy or work done L L L -- p2 ds+ jFsds+ {ws2ds 2AE 2E 0 0 0 (1 1.4) PzL PpgL’ + (pg)’AL3 2AE 2E 6E +--- - -- The last two terms are therefore the modifying terms to eqn. (1 1.1) to account for the body-weight effect of the bar. 11.2. Strain energy-shear Consider the elemental bar now subjected to a shear load Q at one end causing deformation through the angle y (the shear strain) and a shear deflection 6, as shown in Fig. 11.3. Now .. tQ Fig. 11.3. Shear. Strain energy U = work done = 3QS = 3Qyds shear stress t Q shear strain y yA G= =-=- Q y=- AG Q shear strain energy = 3Q x - x ds = ds AG 2AG
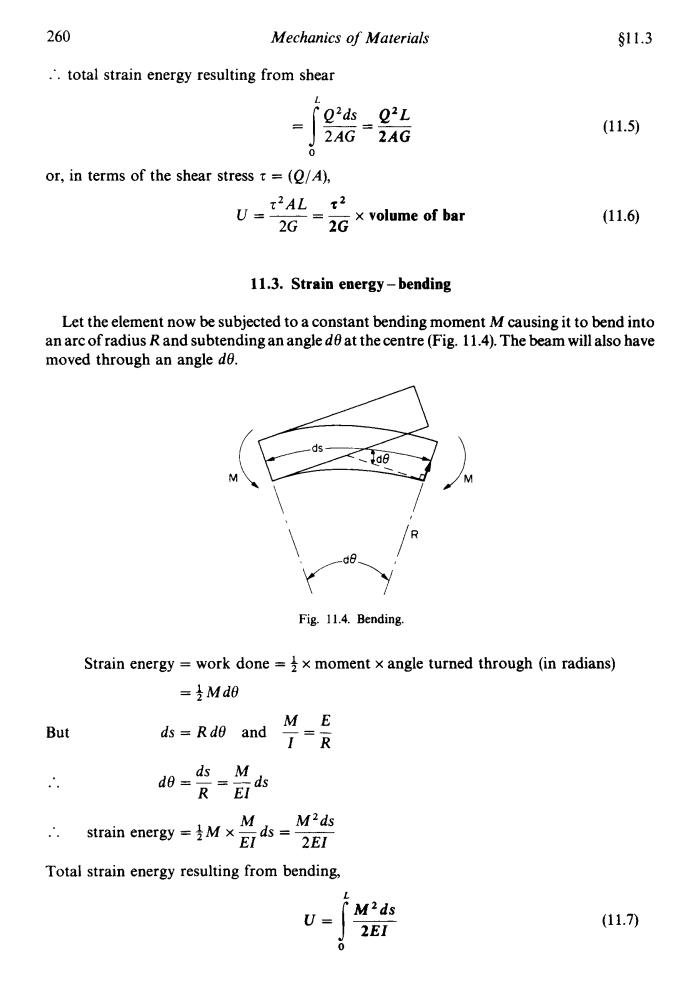
260 Mechanics of Materials §11.3 .'total strain energy resulting from shear o'ds Q2L 2AG 2AG (11.5) or,in terms of the shear stresst =(O/A), 2AL t2 U= 2G=2G×volume of bar (11.6) 11.3.Strain energy-bending Let the element now be subjected to a constant bending moment M causing it to bend into an arc of radius R and subtending an angle de at the centre(Fig.11.4).The beam will also have moved through an angle de. .1d8 M R Fig.11.4.Bending. Strain energy work done =x moment x angle turned through (in radians) =是Md0 ME But ds=Rde and T-R do dsM ds R=E团 M2ds strain energy=支Mx M ds= EI 2EI Total strain energy resulting from bending, L M2ds U= (11.7) 2EI
260 Mechanics of Materials 01 1.3 :. total strain energy resulting from shear L or, in terms of the shear stress 5 = (Q/A), T2~~ z2 ty=-- -- x volume of bar 2G 2G (11.5) (11.6) 11.3. Strain energy -bending Let the element now be subjected to a constant bending moment M causing it to bend into an arc of radius R and subtending an angle de at the centre (Fig. 11.4). The beam will also have moved through an angle de. M \ I But Fig. 11.4. Bending. Strain energy = work done = x moment x angle turned through (in radians) = $ Md0 ME ds = Rd0 and -=- IR M M’ds strain energy = 3M x -ds = ~ EI 2EI ... Total strain energy resulting from bending, (11.7)

§11.4 Strain Energy 261 If the bending moment is constant this reduces to M2L U= 2EI 11.4.Strain energy-torsion The element is now considered subjected to a torque T as shown in Fig.11.5,producing an angle of twist de radians. ds de., Fig.11.5.Torsion. Strain energy work done =iTde But,from the simple torsion theory, T Gde Tds Jds and do= GJ .'total strain energy resulting from torsion, CT2ds T2L U= (11.8) 2GJ 2GJ since in most practical applications T is constant. For a hollow circular shaft eqn.(11.8)still applies T2L i.e. Strain energy U=2GJ Now,from the simple bending theory Tt Tmax 了,=R where R is the outer radius of the shaft and J= 5(R4-r4) π T-2Rtma (R)
91 1.4 Strain Energy 26 1 If the bending moment is constant this reduces to 11.4. Strain energy - torsion The element is now considered subjected to a torque T as shown in Fig. 11.5, producing an angle of twist dO radians. Fig. 11.5. Torsion. Strain energy = work done = 3TdO But, from the simple torsion theory, Tds and dO =- T GdO J ds GJ - .'. total strain energy resulting from torsion, T2ds T2L 2GJ 2GJ 0 since in most practical applications T is constant. For a hollow circular shaji eqn. (1 1.8) still applies T~L Strain energy U = - 2GJ i.e. Now, from the simple bending theory T 7 Tmax - - -- -- JrR where R is the outer radius of the shaft and 7t J=-(R4-r4) 2 (11.8)

262 Mechanics of Materials $11.5 Substituting in the strain energy equation(11.8)we have: (R)L 2R U 20a*-r内 txπ(R4-r)L = 4G R2 []x volume of shaft 4G R2 Strain energy/unit volume= tx [R2+r2] or 4G R2 (11.8a) It should be noted that in the four types of loading case considered above the strain energy expressions are all identical in form, (applied“load")2×L i.e. strain energy Uxproduct of two related constants the constants being related to the type of loading considered.In bending,for example,the relevant constants which appear in the bending theory are Eand I,whilst for torsion Gand J are more applicable.Thus the above standard equations for strain energy should easily be remembered. 11.5.Strain energy of a three-dimensional principal stress system The reader is referred to $14.17 for the derivation of the following expression for the strain energy of a system of three principal stresses: 1 V=2E[i+ai+号-2w(a1o+a+o3i】per unit volume It is then shown in $14.17 that this total strain energy can be conveniently considered as made up of two parts: (a)the volumetric or dilatational strain energy; (b)the shear or distortional strain energy. 11.6.Volumetric or dilatational strain energy This is the strain energy associated with a mean or hydrostatic stress of (+2+3)=actingequally in all three mutually perpendicular directions giving rise to no distortion,merely a change in volume. Then from eqn.(14.22), volumetric strain energy-[(1++03)2]per unit volume
262 Mechanics of Materials $1 1.5 Substituting in the strain energy equation (1 1.8) we have: [%(R4-r4)] 2 L U= x 2G-(R4-r4) zLx z(R4 - r4)L 4G R2 2 -- tLx [Rz +r2] 4G R2 -- x volume of shaft or zLax [R2 +r2] 4G R2 Strain energy/unit volume = - (11.8a) It should be noted that in the four types of loading case considered above the strain energy expressions are all identical in form, i.e. (applied “load”)’ x L 2 x product of two related constants strain energy U = the constants being related to the type of loading considered. In bending, for example, the relevant constants which appear in the bending theory are E and I, whilst for torsion G and J are more applicable. Thus the above standard equations for strain energy should easily be remembered. 11.5. Strain energy of a three-dimensional principal stress system The reader is referred to $14.17 for the derivation of the following expression for the strain energy of a system of three principal stresses: v=-[ a: + ai + 63 - 2v(ala2 + a263 + a3a1)] per unit volume 1 2E It is then shown in $14.17 that this total strain energycan beconvenientlyconsidered as made up of two parts: (a) the volumetric or dilatational strain energy; (b) the shear or distortional strain energy. 11.6. Volumetric or dilatational strain energy This is the strain energy associated with a mean or hydrostatic stress of $(a, + o2 + os) = 0 acting equally in all three mutually perpendicular directions giving rise to no distortion, merely a change in volume. Then from eqn. (14.22), (1 - 2v) volumetric strain energy = ___ [(al + a2 + a3)’] per unit volume 6E

S11.7 Strain Energy 263 11.7.Shear or distortional strain energy In order to consider the general principal stress case it has been shown necessary,in $14.6, to add to the mean stress in the three perpendicular directions,certain so-called deviatoric stress values to return the stress system to values of o,o2 and o3.These deviatoric stresses are then associated directly with change of shape,i.e.distortion,without change in volume and the strain energy associated with this mechanism is shown to be given by shear strain energy-2[(()]per unit volume 6G[oi+吃+of-(a12+a2o3+a3o,】per unit volume This equation is used as the basis of the Maxwell-von Mises theory of elastic failure which is discussed fully in Chapter 15. 11.8.Suddenly applied loads If a load Pis applied gradually to a bar to produce an extension the load-extension graph will be as shown in Fig.11.1 and repeated in Fig.11.6,the work done being given by U=P6. Lood Work done gradually applied load) .P8 Work done suddenly applied load) Extension P‘8 Fig.11.6.Work done by a suddenly applied load. If now a load P'is suddenly applied(i.e.applied with an instantaneous value,not gradually increasing from zero to P')to produce the same extension o,the graph will now appear as a horizontal straight line with a work done or strain energy =P'8. The bar will be strained by an equal amount o in both cases and the energy stored must therefore be equal, i.e. P'δ=支P8 or P=P Thus the suddenly applied load which is required to produce a certain value of instantaneous strain is half the equivalent value of static load required to perform the same function.It is then clear that vice versa a load P which is suddenly applied will produce twice the effect of the same load statically applied.Great care must be exercised,therefore,in the design
$11.7 Strain Energy 263 11.7. Shear or distortional strain energy In order to consider the general principal stress case it has been shown necessary, in 5 14.6, to add to the mean stress 5 in the three perpendicular directions, certain so-called deviatoric stress values to return the stress system to values of al, a’ and a3. These deuiatoric stresses are then associated directly with change of shape, i.e. distortion, without change in volume and the strain energy associated with this mechanism is shown to be given by 1 12G 1 6G shear strain energy = __ [(a, - a’)’ + (a2 - a3)’ + (a3 - ol)’] = - [u: + u: + t~: - (al u2 + u2 uj + uj ul )] per unit volume This equation is used as the basis of the Maxwell-von Mises theory of elastic failure which is discussed fully in Chapter 15. per unit volume 11.8. Suddenly applied loads If a load Pis applied gradually to a bar to produce an extension 6 the load-extension graph will be as shown in Fig. 11.1 and repeated in Fig. 11.6, the work done being given by u = iP6. Fig. 11.6. Work done by a suddenly applied load. If now a load P’ is suddenly applied (i.e. applied with an instantaneous value, not gradually increasing from zero to P’) to produce the same extension 6, the graph will now appear as a horizontal straight line with a work done or strain energy = P‘6. The bar will be strained by an equal amount 6 in both cases and the energy stored must therefore be equal, i.e. P’6 = 3P6 or p’ = &p Thus the suddenly applied load which is required to produce a certain value of instantaneous strain is half the equivalent value of static load required to perform the same function. It is then clear that vice versa a load P which is suddenly applied will produce twice the effect of the same load statically applied. Great care must be exercised, therefore, in the design