
总SS,=∑y2-C=292+372+.+132-C=2355 ·然后,根据A因素与区组两向表计算主区总SSM,并 分解为区组SSR SS和三部分, -C=122 恩心0101+8+沙 5w-2Z-c.2781256+252 -C=32.67 ab 3×4 58.-27-C-286+2432+257 -C=80.17 rb 3×4
◼ 然后,根据A因素与区组两向表计算主区总SSM,并 分解为区组SSR、SSA和三部分, SST =y −C = 总 2 29 37 13 2355 2 2 2 + ++ − C = 主区总 − = = C b T SS m M 2 122 4 101 85 81 2 2 2 − = + + + C 32.67 2 − = + + = −C = C ab T SS r R 3 4 278 256 252 2 2 2 80.17 3 4 286 243 257 2 2 2 − = + + − = = C C rb TA 2 SSA

SSE,=主区总SSr SSR5SS=122-32.67-80.17=9.16 根据A与B两向表(表13.25)计算处理平方和SS,并分 解为SS4SS和SS4B三部分, 处里S9-27i-C-892+100++44-C-2267 3 7-C_254+278+125°+129 SS8=27 3×3 -C=2179.67 ra SS4B处理SS-SS4SSB-2267-80.17-2179.67=7.16 因而,SSE,=总SS,主区总SSy SSB SS4B2355-122-2179.67 -7.16=46.17
= Ea SS 主区总SSM -SSR -SSA =122-32.67-80.17=9.16 根据A与B两向表(表13.25)计算处理平方和SSt,并分 解为SSA、SSB和SSAB三部分, 处理 2267 2 − = + + + − = = C C r T SS A B t 3 89 100 44 2 2 2 SS 2179.67 2 B − = + + + − = = C C ra TB 3 3 254 278 125 129 2 2 2 2 SSAB =处理 SSt -SSA -SSB=2267-80.17-2179.67=7.16 因而, = Eb SS 总SST -主区总SSM -SSB -SSAB =2355-122-2179.67 -7.16 = 46.17
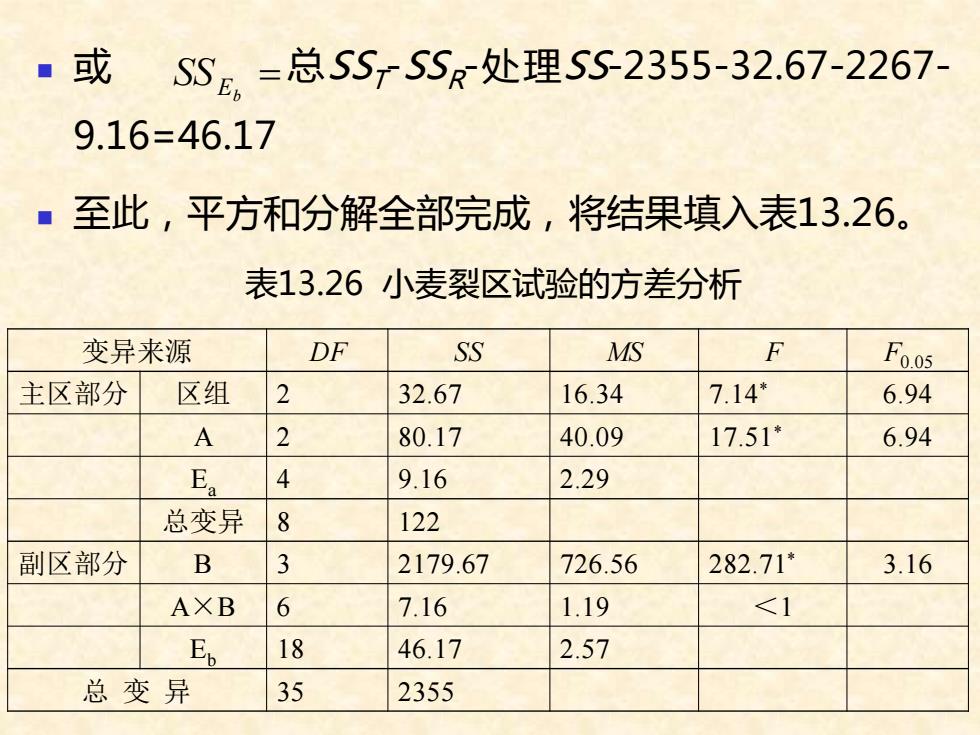
■或 SSe-总SSrSSR处理SS2355-32.67-2267- 9.16=46.17 ■至此,平方和分解全部完成,将结果填入表13.26。 表13.26小麦裂区试验的方差分析 变异来源 DF SS MS F Foos 主区部分 区组 2 32.67 16.34 7.14* 6.94 A 2 80.17 40.09 17.51* 6.94 E 4 9.16 2.29 总变异8 122 副区部分 B 3 2179.67 726.56 282.71* 3.16 AXB 6 7.16 1.19 <1 E 18 46.17 2.57 总变异 35 2355
◼ 或 总SST -SSR -处理SS-2355-32.67-2267- 9.16=46.17 ◼ 至此,平方和分解全部完成,将结果填入表13.26。 表13.26 小麦裂区试验的方差分析 = Eb SS 变异来源 DF SS MS F F0.05 主区部分 区组 2 32.67 16.34 7.14* 6.94 A 2 80.17 40.09 17.51* 6.94 Ea 4 9.16 2.29 总变异 8 122 副区部分 B 3 2179.67 726.56 282.71* 3.16 A×B 6 7.16 1.19 <1 Eb 18 46.17 2.57 总 变 异 35 2355

(3)F测验 ■表13.26中,E是主区误差,Eb为副区误差。当选用 固定模型时,E可用以测验区组间和主处理(A)水平 间均方的显著性;E可用以测验副处理(B)水平间和 A×B互作均方的显著性。由表13.26得到:区组间、 A因素水平间、B因素水平间均有显著差异,但A×B 互作不显著。 ■由此说明:①本试验的区组在控制土壤肥力上有显 著效果,从而显著地减小了误差; ■②不同的中耕次数间有显著差异;
◼ (3) F 测验 ◼ 表13.26中,Ea是主区误差,Eb为副区误差。当选用 固定模型时,Ea可用以测验区组间和主处理(A)水平 间均方的显著性;Eb可用以测验副处理(B)水平间和 A×B互作均方的显著性。由表13.26得到:区组间、 A因素水平间、B因素水平间均有显著差异,但A×B 互作不显著。 ◼ 由此说明:① 本试验的区组在控制土壤肥力上有显 著效果,从而显著地减小了误差; ◼ ② 不同的中耕次数间有显著差异;

■③不同的施肥量间有显著差异; ■④中耕的效应不因施肥量多少而异,施肥量的效应 也不因中耕次数多少而异。 ■(4)效应和互作的显著性测验 ■在此以亩产量进行测验。 ■①中耕次数间表13.25各个T值为rb=3×4=12区产 量之和,故 ■c666.7/(12×33)=1.6835 ·据此可算得各中耕牧处理的亩产量于表13.27。求得亩
◼ ③ 不同的施肥量间有显著差异; ◼ ④ 中耕的效应不因施肥量多少而异,施肥量的效应 也不因中耕次数多少而异。 ◼ (4) 效应和互作的显著性测验 ◼ 在此以亩产量进行测验。 ◼ ① 中耕次数间 表13.25各个TA值为rb=3×4=12区产 量之和,故 ◼ cf=666.7/(12×33)=1.6835 ◼ 据此可算得各中耕处理的亩产量于表13.27。求得亩