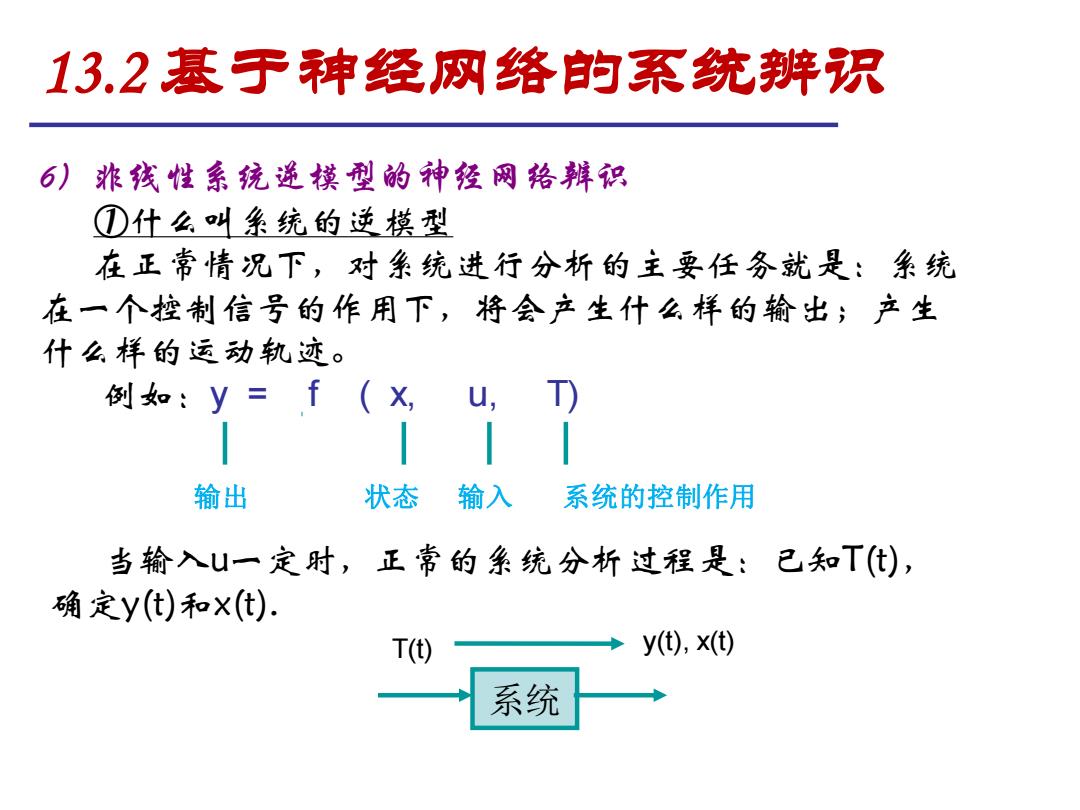
13.2基于神经网络的系统辨识 6)非线性系统进模型的神经网络辨识 ①什么叫条统的逆模型 在正常情况下,对系统进行分析的主要任务就是:系统 在一个控制信号的作用下,将会产生什么样的输出;产生 什么样的运动轨迹。 例如:y=f(X, u D) 输出 状态 输入 系统的控制作用 当输入U一定时,正常的系统分析过程是:已知T(), 确定y(t)和X(t). T(t) y),x) 系统
6)非线性系统逆模型的神经网络辨识 ①什么叫系统的逆模型 在正常情况下,对系统进行分析的主要任务就是:系统 在一个控制信号的作用下,将会产生什么样的输出;产生 什么样的运动轨迹。 例如:y = f ( x, u, T) 输出 状态 输入 系统的控制作用 当输入u一定时,正常的系统分析过程是:已知T(t), 确定y(t)和x(t). 系统 T(t) y(t), x(t) 13.2 基于神经网络的系统辨识
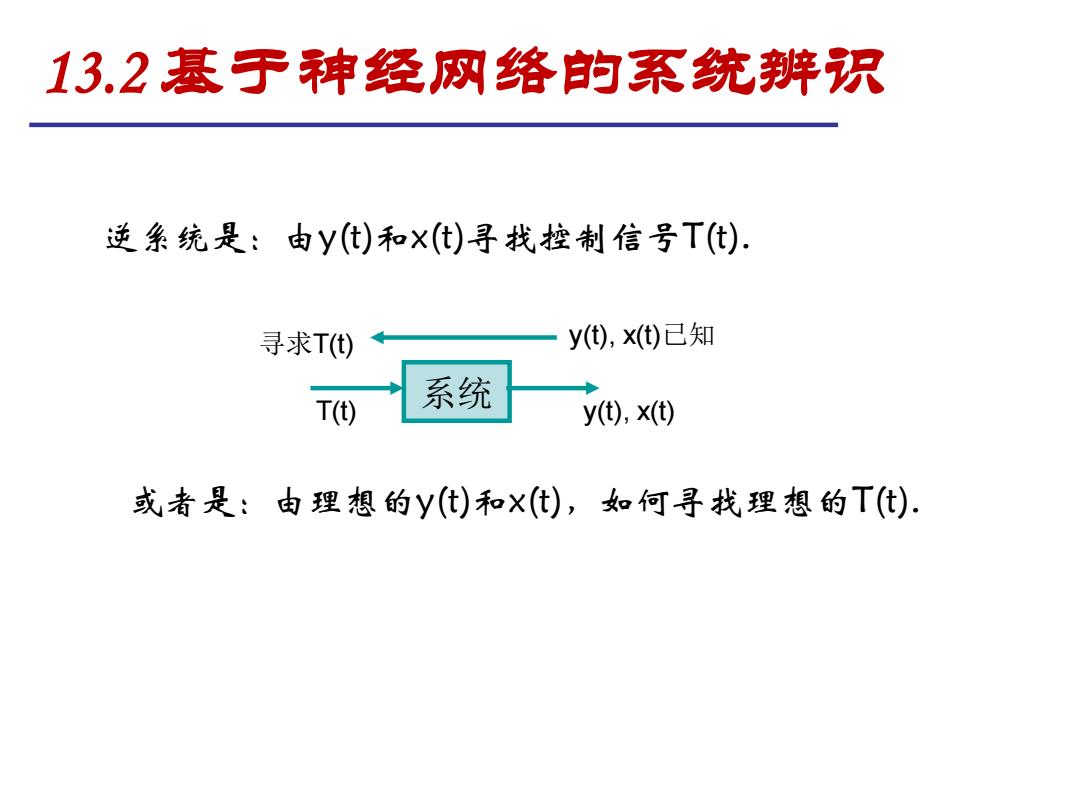
13.2基于神经网络的系统辨识 逆系统是:由y(t)和X(t)寻找控制信号T(t). 寻求T() y(),)已知 T(t) 系统 y(),x) 或者是:由理想的y(t)和X(t),如何寻找理想的T(t)
逆系统是:由y(t)和x(t)寻找控制信号T(t). 系统 寻求T(t) y(t), x(t)已知 T(t) y(t), x(t) 或者是:由理想的y(t)和x(t),如何寻找理想的T(t). 13.2 基于神经网络的系统辨识

13,2基于神经网络的系统辨况 ②系统分析逆模型的存在性 在一个控制系统中,如果已知了运动的轨迹y(t)、X(t)要想 求出它的控制信号T(t),首先必然要知道这个控制信号是否存 在?系统是否可逆? 线型系统的可逆性问题实际上是一个能控性问题,即线性 可控系统即是可逆系统。非线性则未必。但有如下定理存在: 定理:如果对于u(k),f[y(k)y(k-n),u(k)…u(k-m)]严格 单调,那么系统在点y(k)y(k-n),u(k)…u(k-m)]T处可逆。 只有在所有点处可逆都成立,系统才是可逆的。 ③非线性系统的逆模型 非线性系统的逆模型研究包括逆系统建模和逆模型辨识两 部分内容。逆系统建模是对非线性系统的逆运行过程建立一数 学模型。逆模型辨识是对非线性系统的逆运行进行辨识识别, 看其与哪种已知模型更接近
②系统分析逆模型的存在性 在一个控制系统中,如果已知了运动的轨迹y(t)、x(t)要想 求出它的控制信号T(t),首先必然要知道这个控制信号是否存 在?系统是否可逆? 线型系统的可逆性问题实际上是一个能控性问题,即线性 可控系统即是可逆系统。非线性则未必。但有如下定理存在: 定理:如果对于u(k), f [y(k) …y(k-n), u(k) …u(k-m)] 严格 单调,那么系统在点[y(k) …y(k-n), u(k) …u(k-m)] T 处可逆。 只有在所有点处可逆都成立,系统才是可逆的。 ③非线性系统的逆模型 非线性系统的逆模型研究包括逆系统建模和逆模型辨识两 部分内容。逆系统建模是对非线性系统的逆运行过程建立一数 学模型。逆模型辨识是对非线性系统的逆运行进行辨识识别, 看其与哪种已知模型更接近。 13.2 基于神经网络的系统辨识
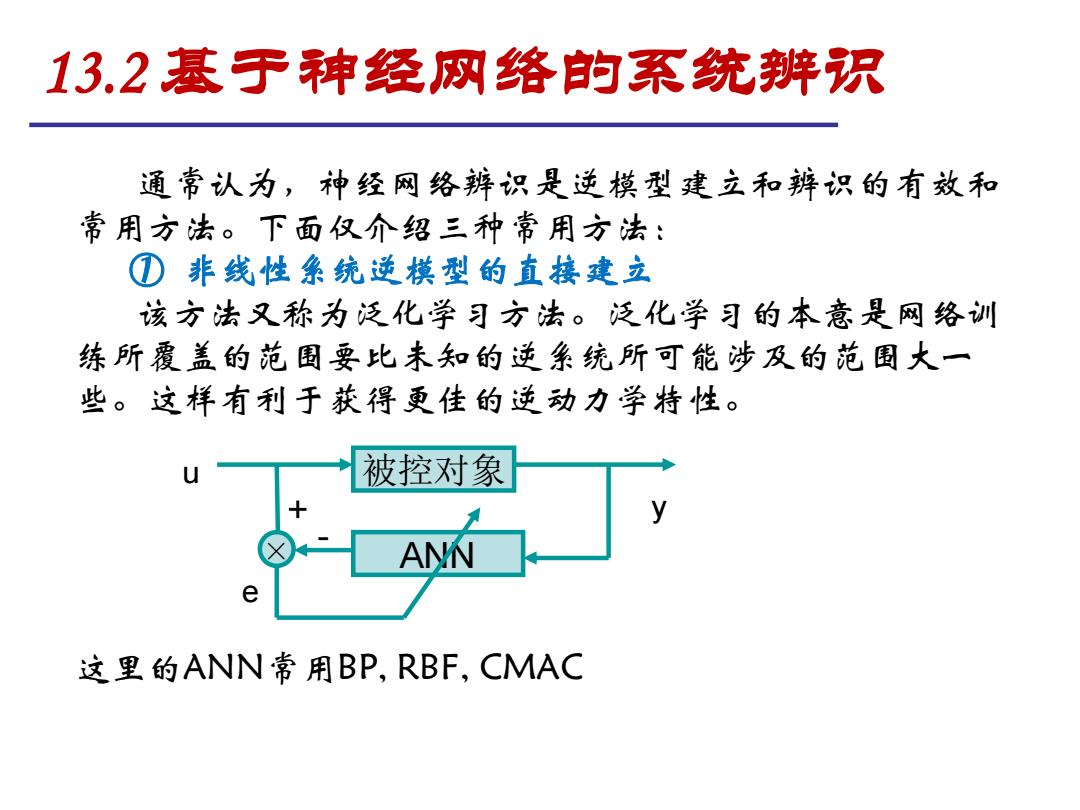
13.2基于神经网络的系统辨识 通常认为,神经网络辨识是逆模型建立和辨识的有效和 常用方法。下面仅介绍三种常用方法: ①非线性条统逆模型的直接建立 该方法又称为泛化学习方法。泛化学习的本意是网络训 练所覆盖的范围要比未知的逆系统所可能涉及的范围大一 些。这样有利于获得更佳的逆动力学特性。 被控对象 ANN 这里的ANN常用BP,RBF,CMAC
通常认为,神经网络辨识是逆模型建立和辨识的有效和 常用方法。下面仅介绍三种常用方法: ① 非线性系统逆模型的直接建立 该方法又称为泛化学习方法。泛化学习的本意是网络训 练所覆盖的范围要比未知的逆系统所可能涉及的范围大一 些。这样有利于获得更佳的逆动力学特性。 被控对象 - ANN + e × u y 这里的ANN常用BP, RBF, CMAC 13.2 基于神经网络的系统辨识
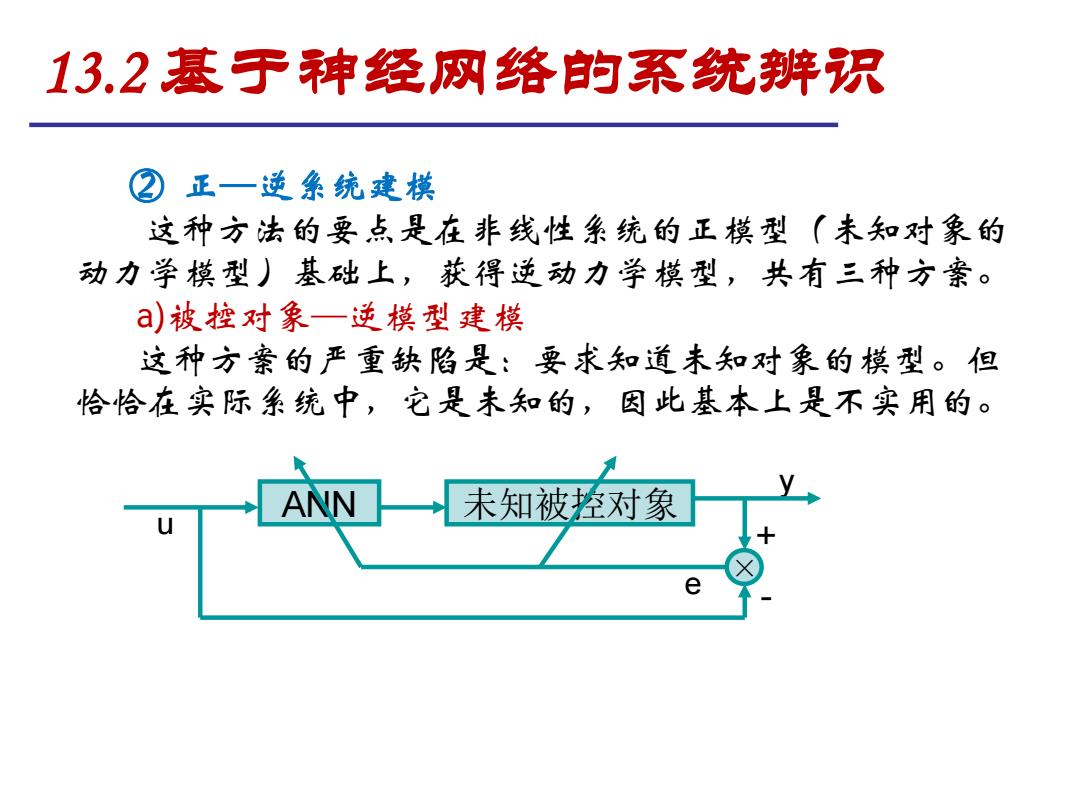
13.2基于神经网络的系统辨识 正一逆条统建模 这种方法的要点是在非线性系统的正模型(未知对象的 动力学模型)基础上,获得逆动力学模型,共有三种方亲。 a)被控对象一逆模型建模 这种方案的严重缺陷是:要求知道未知对象的模型。但 恰恰在实际系统中,它是未知的,因此基本上是不实用的。 ANN 未知被控对象 e
② 正—逆系统建模 这种方法的要点是在非线性系统的正模型(未知对象的 动力学模型)基础上,获得逆动力学模型,共有三种方案。 a)被控对象—逆模型建模 这种方案的严重缺陷是:要求知道未知对象的模型。但 恰恰在实际系统中,它是未知的,因此基本上是不实用的。 未知被控对象 - ANN + e × u y 13.2 基于神经网络的系统辨识