
13,2基于神经网络的系统辨况 5)辨识系统中的脓线性模型 神经网络作系统辨识,主要用于非线性辨识和自适应。 由于非线性系统在能控性、能观性、负反馈调节、状态观 测器设计等方面还没有成熟的作法。难度是非线性系统的 辨识模型和控制模型不易选取,为此,用神经网络辨识非 线性系统必须作一些假设限制: √被控对象具有能控性、能观性。 √对所有可能的输入控制量U,被控对象的输出y存在并 有界。 √在辨识模型中的神经网络允许一个或几个不同的神经 网络结构用于被控对象。 √辨识模型的基本结构为包会神经网络的串一并联结构
5)辨识系统中的非线性模型 神经网络作系统辨识,主要用于非线性辨识和自适应。 由于非线性系统在能控性、能观性、负反馈调节、状态观 测器设计等方面还没有成熟的作法。难度是非线性系统的 辨识模型和控制模型不易选取,为此,用神经网络辨识非 线性系统必须作一些假设限制: ✓被控对象具有能控性、能观性。 ✓对所有可能的输入控制量u,被控对象的输出y存在并 有界。 ✓在辨识模型中的神经网络允许一个或几个不同的神经 网络结构用于被控对象。 ✓辨识模型的基本结构为包含神经网络的串—并联结构。 13.2 基于神经网络的系统辨识

13.2基于神经网络的系统辨识 前两条为保证条统的稳定性和可辨性,第三条为了方 便选择模型,简化处理过程,第四条限制主要是为了易于 达到以下目的: >由于输出y存在并有界,那么串一并联模型中的所有 信号均有界,辨识模型易于稳定。 >串一并联模型间无反馈,使从后向前的静态反向传输 算法成为可能。 >当误差足够小时,不使用串一并联结构,只用并联结 构也能有好的效果。 在前述四种假设限制下,能够写出常用的一些非线性 典型模型,现举例如下:
前两条为保证系统的稳定性和可辨性,第三条为了方 便选择模型,简化处理过程,第四条限制主要是为了易于 达到以下目的: ➢由于输出y存在并有界,那么串—并联模型中的所有 信号均有界,辨识模型易于稳定。 ➢串—并联模型间无反馈,使从后向前的静态反向传输 算法成为可能。 ➢当误差足够小时,不使用串—并联结构,只用并联结 构也能有好的效果。 在前述四种假设限制下,能够写出常用的一些非线性 典型模型,现举例如下: 13.2 基于神经网络的系统辨识

13.2基于神经网络的系统辨识 n-1 yk+I)=∑a,y(k-i)+g(u(k)u(k-1)…(k-m) i=0 n=2,m=0时的并联结构如图3所示。 y(k+1) u(k) e(k+1) 图3并联结构
n=2,m=0时的并联结构如图3所示。 1 0 ( 1) ( ) ( ( ) ( 1) ( )) n i i y k a y k i g u k u k u k m − = + = − + − − u(k) - e(k+1) + + × Z-1 × a0 a1 Z-1 + + N + Z-1 ∑ a0 a1 Z-1 + + g + ∑ × + y(k+1) 图3 并联结构 ① 13.2 基于神经网络的系统辨识
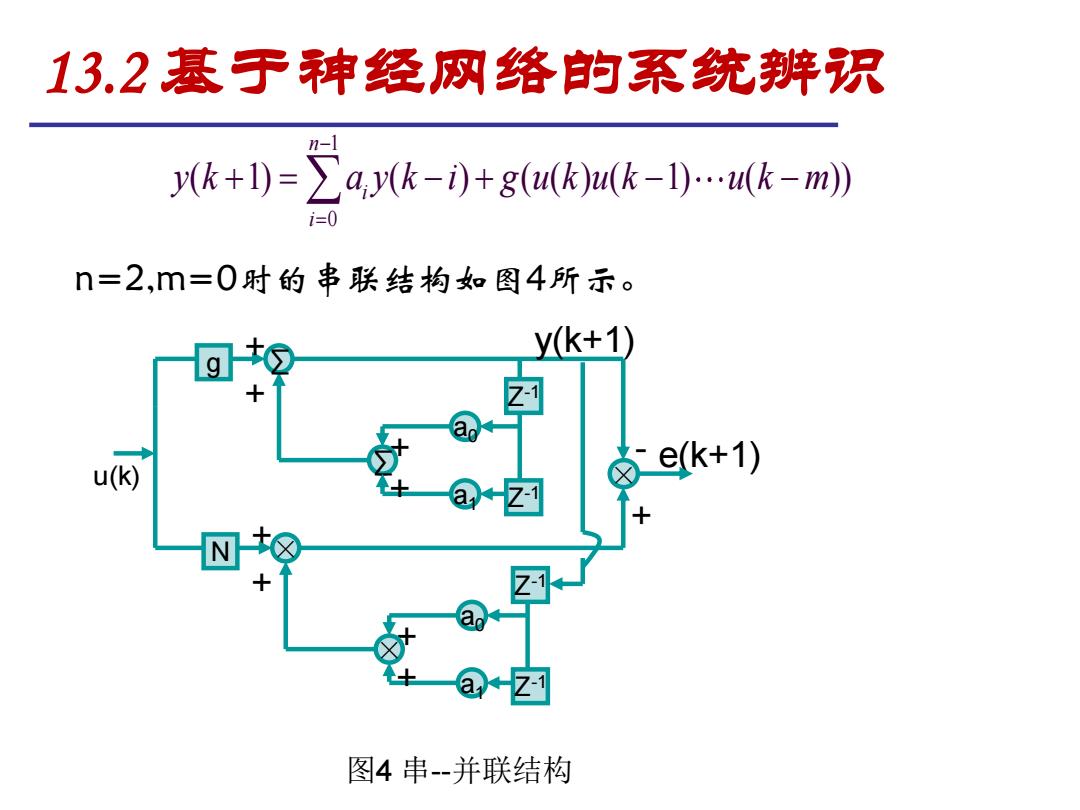
13.2基于神经网络的系统辨识 n-1 yk+1)=∑ayk-i)+g((K)uk-1)…k-m) i=0 n=2,m=0时的串联结构如图4所示。 yk+1) u(k) 卤ek+1) @Z函 图4串-并联结构
n=2,m=0时的串联结构如图4所示。 1 0 ( 1) ( ) ( ( ) ( 1) ( )) n i i y k a y k i g u k u k u k m − = + = − + − − u(k) - e(k+1) + + × Z-1 × a0 a1 Z-1 + + N + Z-1 ∑ a0 a1 Z-1 + + g + ∑ × + y(k+1) 图4 串--并联结构 13.2 基于神经网络的系统辨识

13.2基于神经网络的系统辨识 y(k+1)=∑b,(k-i)+f(y(k)y(k-1)…y(k-n) i=l ②结构同图3、图4,将8换为f. y(k+1)=f(gk)…g(k-n)+g(u(k)…(k-m) y(k+1)=f(y(k)…g(k-n),u(k)…u(k-m) 后两种用神经网络实现起来较难
②结构同图3、图4,将g换为f. y k f g k g k n g u k u k m ( 1) ( ( ) ( )) ( ( ) ( )) + = − + − 1 ( 1) ( ) ( ( ) ( 1) ( )) m i i y k b u k i f y k y k y k n = ② + = − + − − ③ ④ y k f y k g k n u k u k m ( 1) ( ( ) ( ), ( ) ( )) + = − − 后两种用神经网络实现起来较难。 13.2 基于神经网络的系统辨识