
13.2基于神经网络的系统辨识 b)正模型一逆系统建模 其中的正模型是指X→y之间的映射(整个系统是单位反馈 时才可用)。 这种方案的优点是:正模型建立之后就成为己知条件,未 知被控对象的各种运算都能从正模型中计算出来。 不足之处在于逆模型的精度完全取决于正模型的精度。且 这种缺陷是这种辨识结构所设。 X ANN 被控对象 y 正模型
b)正模型—逆系统建模 其中的正模型是指x→y之间的映射(整个系统是单位反馈 时才可用)。 这种方案的优点是:正模型建立之后就成为已知条件,未 知被控对象的各种运算都能从正模型中计算出来。 不足之处在于逆模型的精度完全取决于正模型的精度。且 这种缺陷是这种辨识结构所设。 正模型 - ANN + e × u y 被控对象 x 13.2 基于神经网络的系统辨识
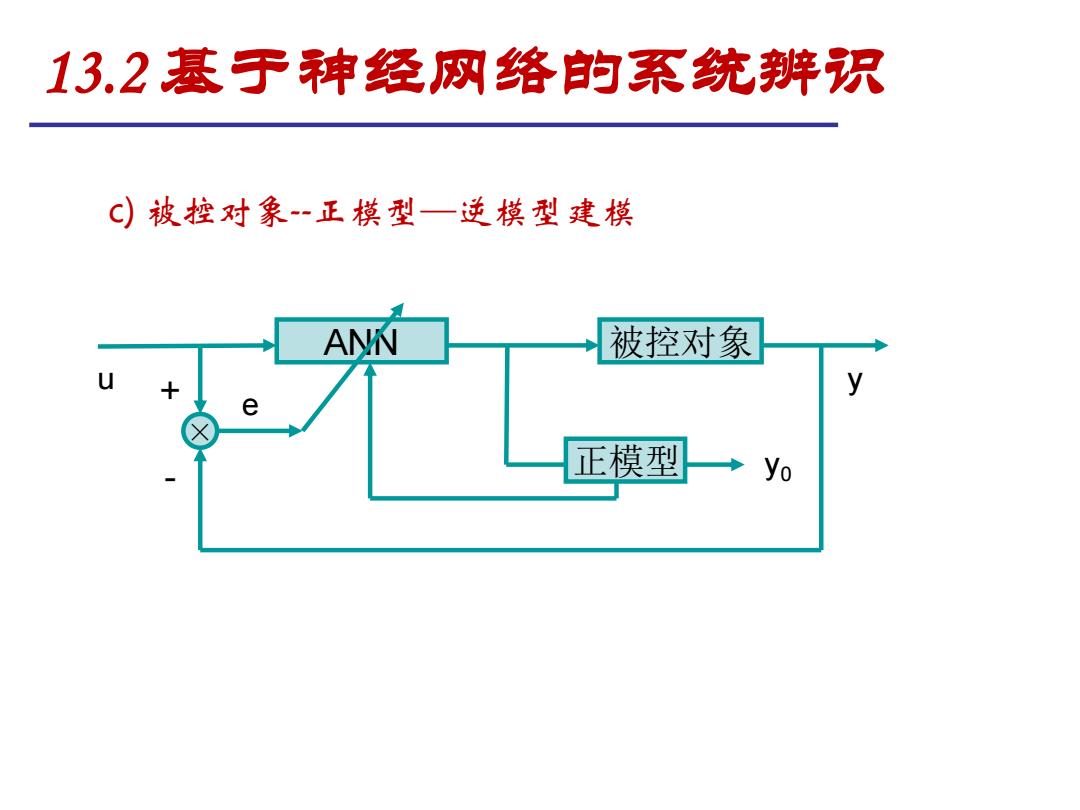
13.2基于神经网络的系统辨识 C)被控对象正模型一逆模型建模 ANN 被控对象 y e 正模型 yo
c) 被控对象--正模型—逆模型建模 - 正模型 ANN + e × u y 被控对象 y0 13.2 基于神经网络的系统辨识

13.3基于神经网络的系统辨识示例 例1线性离散系统辨识示例 仿真系统为二阶S1SO系统,表示为y(k)-1.5y(k-1)+0.7y(k 2)=u(k-1)+0.5u(k-2)。辨识器NNI选择串-并联结构,采用自 适应线性神经元的DTNN网络。 ) 二阶系统 这里的学习算法可采用 一次性LS(离线)和递推LS 及梯度下降法(在线)。 系统输入采用M序列, M序列选用周期Np=15的四 阶M序列。M序列的图形可 见仿真结果。 NNI e可) 学习单法
例1 线性离散系统辨识示例 仿真系统为二阶SISO系统,表示为y(k)-1.5y(k-1)+0.7y(k- 2)=u(k-1)+0.5u(k-2)。辨识器NNI选择串-并联结构,采用自 适应线性神经元的DTNN网络。 这里的学习算法可采用 一次性LS(离线)和递推LS 及梯度下降法(在线)。 系统输入采用M序列, M序列选用周期Np=15的四 阶M序列。M序列的图形可 见仿真结果。 13.3 基于神经网络的系统辨识示例