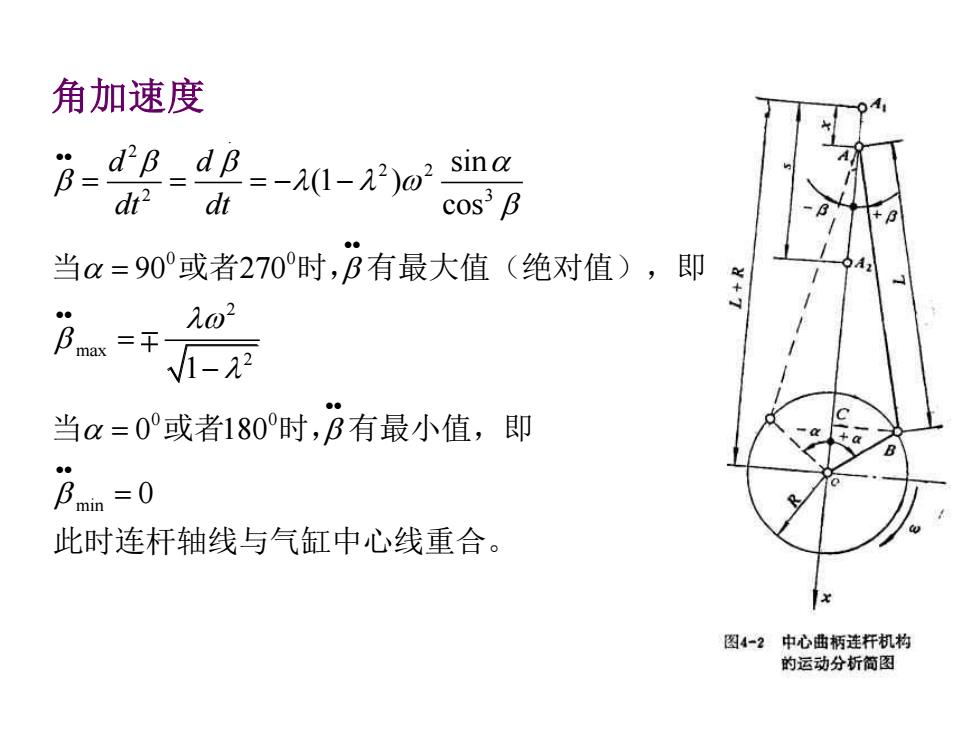
角加速度 月-4B_p-l-2osna dr dt cos3 B 当α=90°或者270时,B有最大值(绝对值),即 B千 Ao2 1-2 当α=0°或者180时,B有最小值,即 ●● in=0 此时连杆轴线与气缸中心线重合。 图4-2中心曲柄连杆机构 的运动分析简图
. 2 2 2 2 3 0 0 2 max 2 0 0 min sin (1 ) cos 90 270 1 0 180 0 d d dt dt •• •• •• •• •• = = = − − = = − = = 当 或者 时, 有最大值(绝对值),即 当 或者 时, 有最小值,即 此时连杆轴线与气缸中心线重合。 角加速度

三、活塞的行程和位移 活塞的行程: s=A0-AO=(L+R)-(L-R)=2R 活塞的位移: x=AA=A0-A0=A0-(CO+AC) =(R+L)-(Rcosa+Lcos B)【精确解】 cosB=V1-sin"a 1-sin"a 2 则:x=R1-cosu+2 sin近似解】 图4-2中心曲柄连杆机构 的运动分析简图
s = A1 O − A2 O = (L + R) − (L − R) = 2R 活塞的行程: 活塞的位移: 1 1 1 ( ) ( ) ( cos cos ) x A A AO AO AO CO AC R L R L = = − = − + = + − + 【精确解】 三、 活塞的行程和位移 2 (1 cos sin ) 2 x R 则: = − + 【近似解】 2 2 2 2 sin 2 1 cos = 1− sin 1−
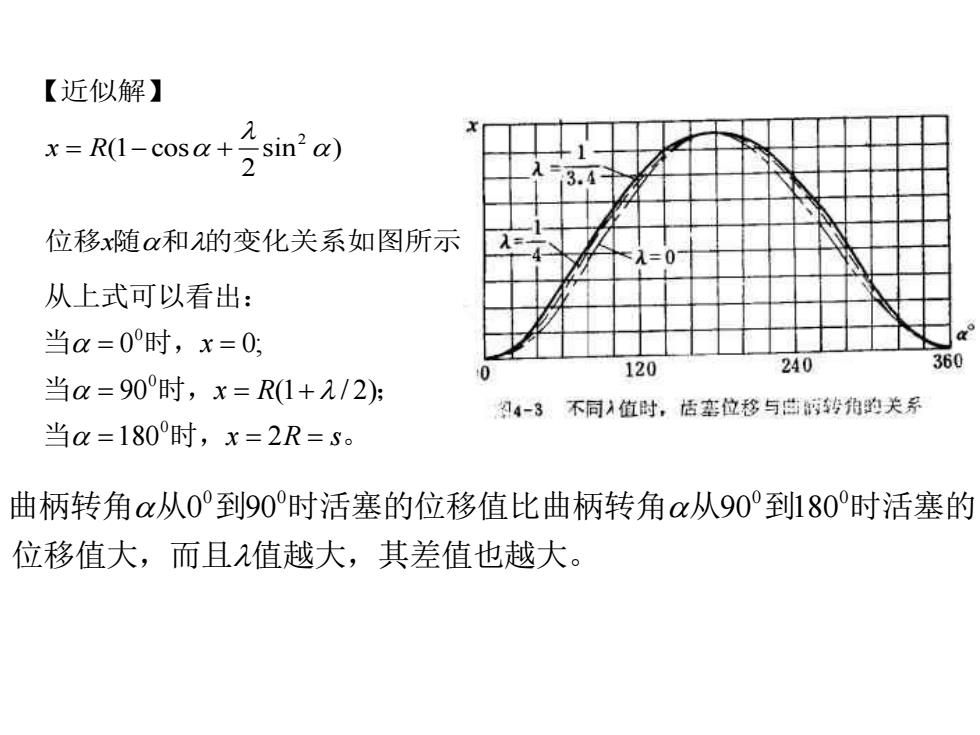
【近似解】 x=R(1-cosa+ 2sin'a) 位移x随α和的变化关系如图所示 入=0 从上式可以看出: 当a=0°时,x=0; 120 240 360 0 当a=90°时,x=R(1+/2)月 幻4-3不同值时,悟塞位移与曲转角跑关系 当a=180°时,x=2R=S。 曲柄转角α从0°到90时活塞的位移值比曲柄转角α从90°到180时活塞的 位移值大,而且几值越大,其差值也越大
2 (1 cos sin ) 2 x R x = − + 【近似解】 位移 随 和 的变化关系如图所示 当 时, 。 当 时, ; 当 时, 从上式可以看出: x R s x R x = = = = = + = = 180 2 90 (1 / 2) 0 0; 0 0 0 0 0 0 0 0 90 90 180 曲柄转角 从 到 时活塞的位移值比曲柄转角 从 到 时活塞的 位移值大,而且 值越大,其差值也越大

四、活塞的速度 将活塞位移的精确解和近似解对时间微分, 可求得活塞速度的精确值和近似值: dxdx da 元sin2o 1= 【精确解】 dt da dt =Ro(sina+ 2 cos B v=Ro(sin a+二sin2a)【近似解】 2
) 【精确解】 cos sin 2 2 (sin = = = R + dt d d dx dt dx v sin 2 ) 【近似解】 2 (sin v = R + 可求得活塞速度的精确值和近似值: 将活塞位移的精确解和近似解对时间t微分, 四、 活塞的速度
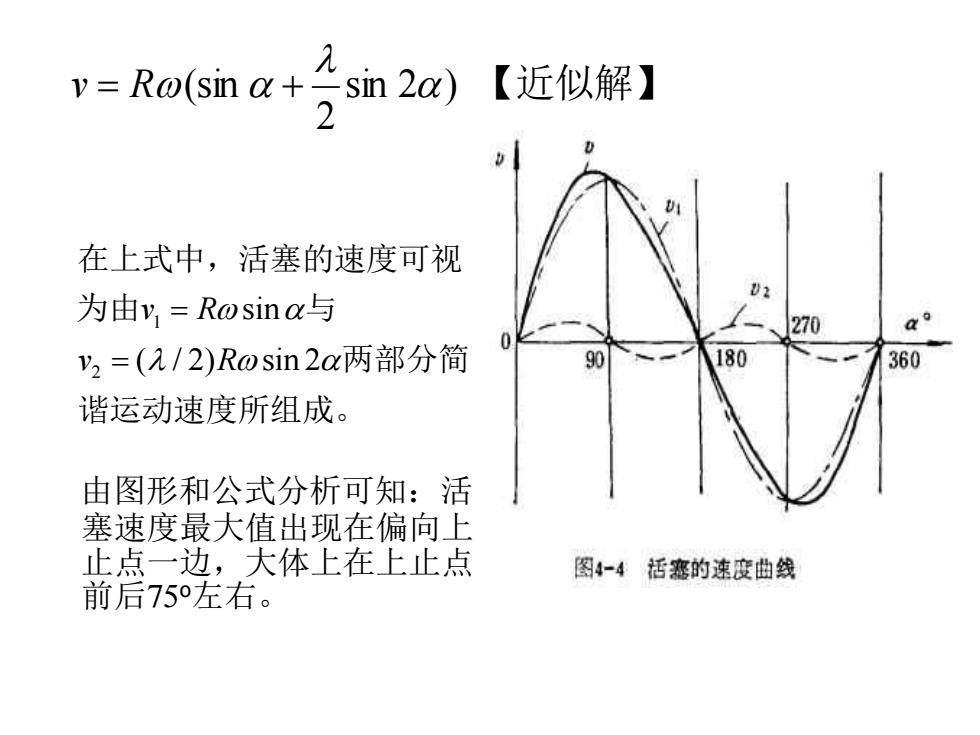
v=Ro(sina+sin2a)【近似解】 在上式中,活塞的速度可视 为由y,=Rosina与 270 Q y2=(2/2)Rosin2a两部分简 180 360 谐运动速度所组成。 由图形和公式分析可知:活 塞速度最大值出现在偏向上 止点一边,大体上在上止点 图4-4活塞的速度曲线 前后75左右
1 2 sin ( / 2) sin 2 v R v R = = 在上式中,活塞的速度可视 为由 与 两部分简 谐运动速度所组成。 由图形和公式分析可知:活 塞速度最大值出现在偏向上 止点一边,大体上在上止点 前后75o左右。 sin 2 ) 【近似解】 2 (sin v = R +