实际模拟带宽只需考虑到100kHz,即此时的o=3π/4,所以真实信号 不会发生混叠,以上设计较为合理。 5)数字下变频(DDC)系统设计 综上,最终实现的数字下变频(DDC)器的结构框图如下: ◇X →HB1↓2HB2I2FIR↓2 0-27 A/D =44NC0 7 400ksps .11 0始20 f=3.2MH吃 +HB1→↓2→HB2→I2IR↓2 步骤2:利用MATLAB工具进行DDC模块设计仿真与验证 1)HB滤波器设计与MATLAB仿真验证 ●HB滤波器设计 通常将HB滤波器设计为奇数阶、偶对称的线性相位FIR滤波器。 设第一级HB滤波器的性能参数为:通带和阻带纹波系数相等,为 6=⊙,=6=0.0001:通带截至频率为a-。;阻带起始频率为 8 on=π:采用窗函数法,选择kaiser窗函数,则滤波器的阶数N为: -201g8-13 N=Ceil 1+ 2.32(041-0)」 -201g0.0001-13 Ceil 1+ 71 2.32不-8) =14 其中Ci[表示取大于计算值的最小整数。这个设计过程可以通过调 用MATLAB函数firhalfband,计算出HB滤波器阶数及其系数,即: -6-
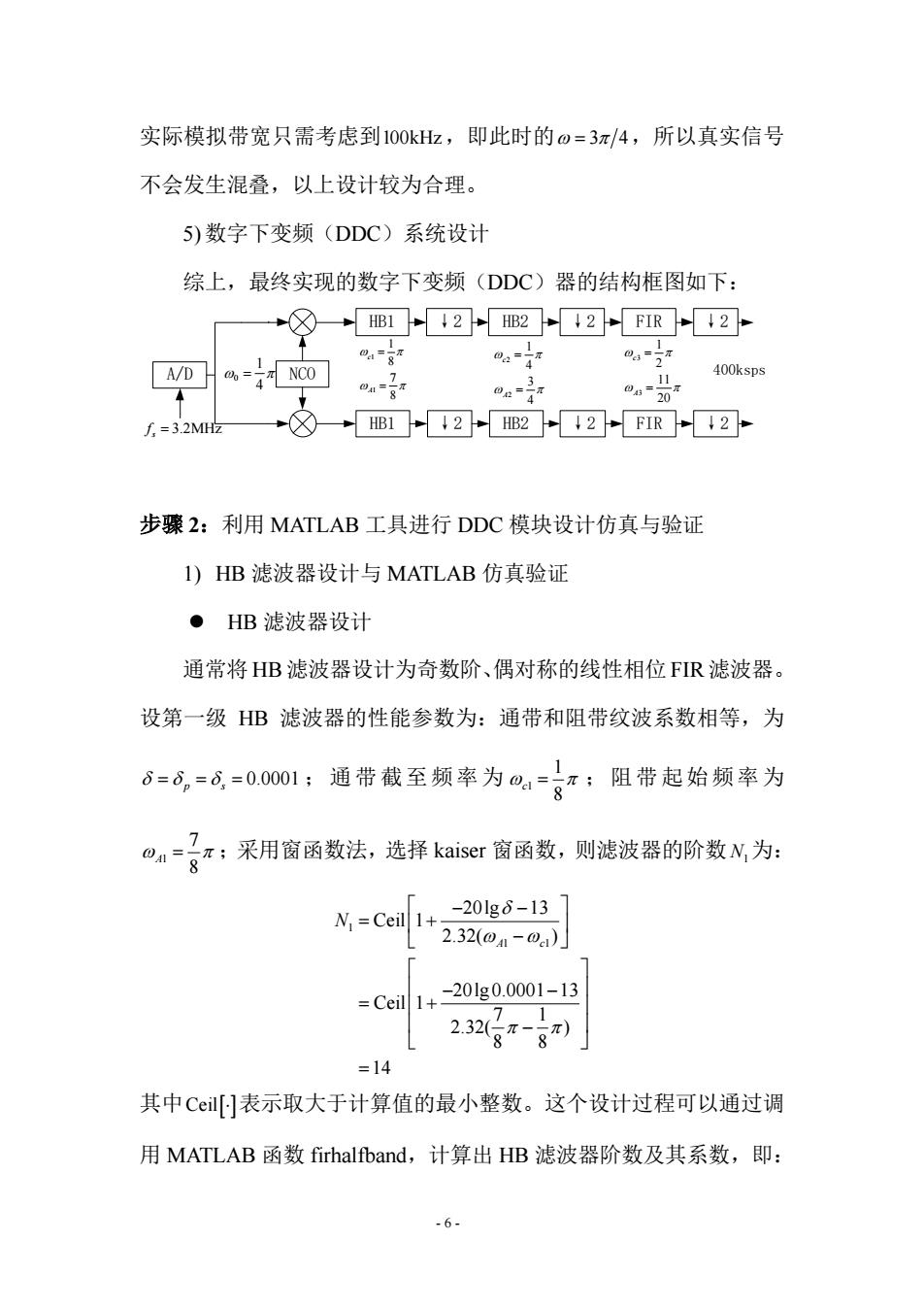
- 6 - 实际模拟带宽只需考虑到100kHz,即此时的ω π = 3 4,所以真实信号 不会发生混叠,以上设计较为合理。 5)数字下变频(DDC)系统设计 综上,最终实现的数字下变频(DDC)器的结构框图如下: NCO HB1 ↓2 HB2 ↓2 FIR ↓2 1 1 1 8 7 8 c A ω π ω π = = 2 2 1 4 3 4 c A ω π ω π = = 3 3 1 2 11 20 c A ω π ω π = = 0 1 4 ω π = 400ksps HB1 ↓2 HB2 ↓2 FIR ↓2 A/D 3.2MHz sf = 步骤 2:利用 MATLAB 工具进行 DDC 模块设计仿真与验证 1) HB 滤波器设计与 MATLAB 仿真验证 HB 滤波器设计 通常将 HB 滤波器设计为奇数阶、偶对称的线性相位 FIR 滤波器。 设第一级 HB 滤波器的性能参数为:通带和阻带纹波系数相等,为 0.0001 p s δδ δ = = = ;通带截至频率为 1 1 8 ω π c = ;阻带起始频率为 1 7 8 ω π A = ;采用窗函数法,选择 kaiser 窗函数,则滤波器的阶数N1为: 1 1 1 20lg 13 Ceil 1 2.32( ) 20lg 0.0001 13 Ceil 1 7 1 2.32( ) 8 8 14 A c N δ ω ω π π − − = + − − − = + − = 其中Ceil[⋅]表示取大于计算值的最小整数。这个设计过程可以通过调 用 MATLAB 函数 firhalfband,计算出 HB 滤波器阶数及其系数,即:
firhalfband(minorder',fp,dev,kaiser') 计算得出的第一级HB滤波器系数: -0.000121531661227744 0 0.0072572726223049146 0 -0.052403932043940268 0 0.29523828385755851 0.5 0.29523828385755851 0 -0.052403932043940268 0 0.0072572726223049146 0 -0.000121531661227744 其频率响应如下图所示: -40 0.5 Frequency (MHz) 同理,可计算出第二级HB滤波器阶数N,=22,滤波器系数为: -0.000077338329872200746 0 0.0016782203783104223 0 -0.0086390482778268378 0 0.028649384427781206 -7
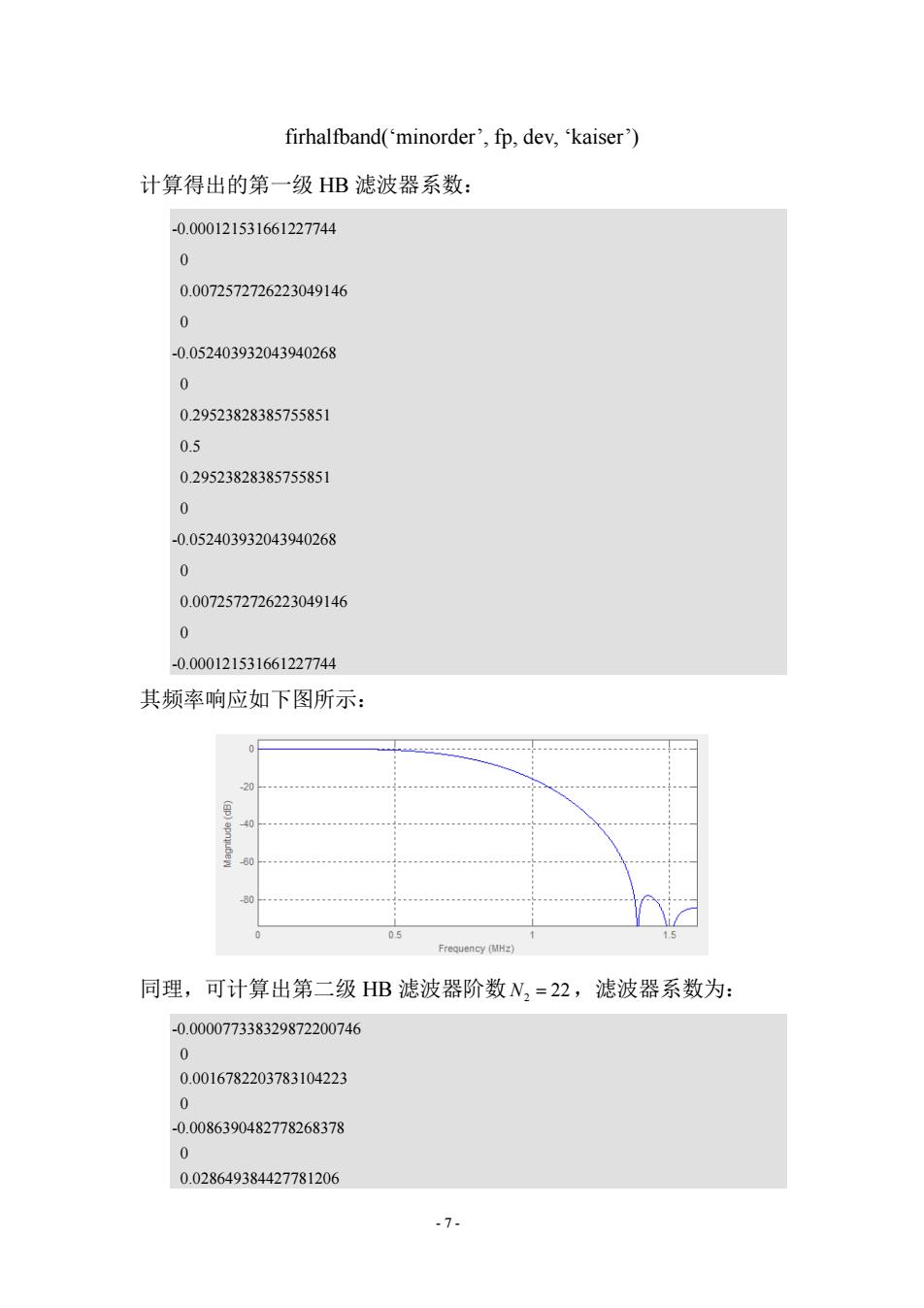
- 7 - firhalfband(‘minorder’, fp, dev, ‘kaiser’) 计算得出的第一级 HB 滤波器系数: -0.000121531661227744 0 0.0072572726223049146 0 -0.052403932043940268 0 0.29523828385755851 0.5 0.29523828385755851 0 -0.052403932043940268 0 0.0072572726223049146 0 -0.000121531661227744 其频率响应如下图所示: 同理,可计算出第二级 HB 滤波器阶数 2 N = 22,滤波器系数为: -0.000077338329872200746 0 0.0016782203783104223 0 -0.0086390482778268378 0 0.028649384427781206
0 -0.0803675193375923 0 0.30878390531578831 0.5 0.30878390531578831 0 -0.0803675193375923 0 0.028649384427781206 0 -0.0086390482778268378 0 0.0016782203783104223 0 -0.000077338329872200746 其频率响应如下图: 20 -60 80 100 200 300 400 500 600 700 Frequency(kHz) ● MATLAB仿真验证 以第一级HB滤波器为例,输入信号模拟频率为0.1MHz,采样率 为3.2MHz,MATLAB仿真波形如下图所示: -8-
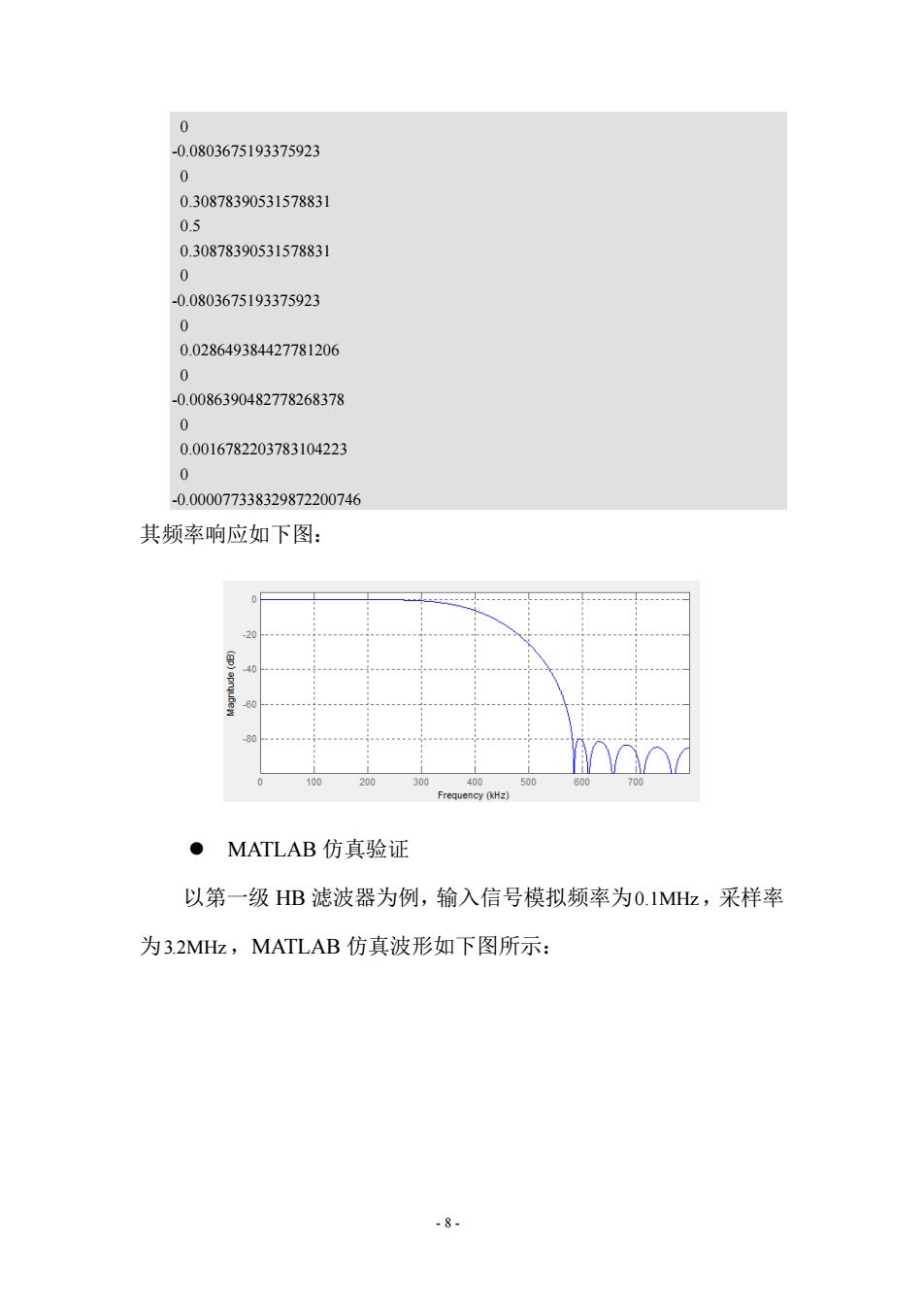
- 8 - 0 -0.0803675193375923 0 0.30878390531578831 0.5 0.30878390531578831 0 -0.0803675193375923 0 0.028649384427781206 0 -0.0086390482778268378 0 0.0016782203783104223 0 -0.000077338329872200746 其频率响应如下图: MATLAB 仿真验证 以第一级 HB 滤波器为例,输入信号模拟频率为0.1MHz,采样率 为3.2MHz,MATLAB 仿真波形如下图所示:

输入信号波形 50 100 150 200250 300 350 半带滤波后信号波形 50 100 150 200 250 300 350 2倍抽取后信号波形 20 40 60 80 100120140160 180 2)第三级FIR滤波器设计与MATLAB仿真 ●第三级FIR滤波器设计 半带滤波器的特殊频率响应,使其很适合于设计2倍抽取的结 构,但是半带滤波器的过渡带一般比较大,因此不太适合作为多级抽 取结构的最后一级,所以会选择截止特性更好,过渡带更窄的其他类 型的FIR滤波器。FIR设计方法通常分为加窗法、频率采样法以及等 纹波逼近法三种,半带滤波器就是等纹波逼近设计方法的一种特例。 相对于其他两种设计方法,等纹波逼近法是基于最大误差最小化准 则,其在整个范围内,逼近误差是均匀分布的,也就是更能逼近所 需滤波器的特性。MATLAB中等纹波最佳误差逼近的滤波器阶数估 计函数为firpmord,系数计算函数为firpm,通过以下代码实现设计, [n f0 a0 w]=firpmord(ff,a,dev); %估计滤波器阶数 [b delta]=firpm(n,fo,a0,w); %计算滤波器系数 -9-
- 9 - 0 50 100 150 200 250 300 350 -1 0 1 输入信号波形 0 50 100 150 200 250 300 350 -1 0 1 半带滤波后信号波形 0 20 40 60 80 100 120 140 160 180 -1 0 1 2倍抽取后信号波形 2) 第三级 FIR 滤波器设计与 MATLAB 仿真 第三级 FIR 滤波器设计 半带滤波器的特殊频率响应,使其很适合于设计 2 倍抽取的结 构,但是半带滤波器的过渡带一般比较大,因此不太适合作为多级抽 取结构的最后一级,所以会选择截止特性更好,过渡带更窄的其他类 型的 FIR 滤波器。FIR 设计方法通常分为加窗法、频率采样法以及等 纹波逼近法三种,半带滤波器就是等纹波逼近设计方法的一种特例。 相对于其他两种设计方法,等纹波逼近法是基于最大误差最小化准 则, 其在整个范围内,逼近误差是均匀分布的,也就是更能逼近所 需滤波器的特性。MATLAB 中等纹波最佳误差逼近的滤波器阶数估 计函数为 firpmord,系数计算函数为 firpm,通过以下代码实现设计, [n f0 a0 w] = firpmord(ff, a, dev); %估计滤波器阶数 [b delta] = firpm(n, f0, a0, w); %计算滤波器系数
其频率响应如下图, ency (Hz) ●MATLAB仿真验证 第三级FIR滤波器输入频率为100kHz,采样率为800kHz, MATLAB仿真波形如下图所示: 输入信号波形 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 28 ×10 FR滤波后信号波形 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 ×10 2倍抽取后信号波形 1.2 1.4 1.6 1.8 2.2 2.4 2.6 2.8 x10 3)数字下变频MATLAB仿真 对输入信号频率为10.1MHz,采样率为3.2MHz,带通采样后得到 的信号为o=5π/16,对应的模拟频率为0.5MHz,编写MATLAB仿真 代码,得到DDC输出的I、Q两路仿真波形,如下图所示。 I路仿真波形为: -10-
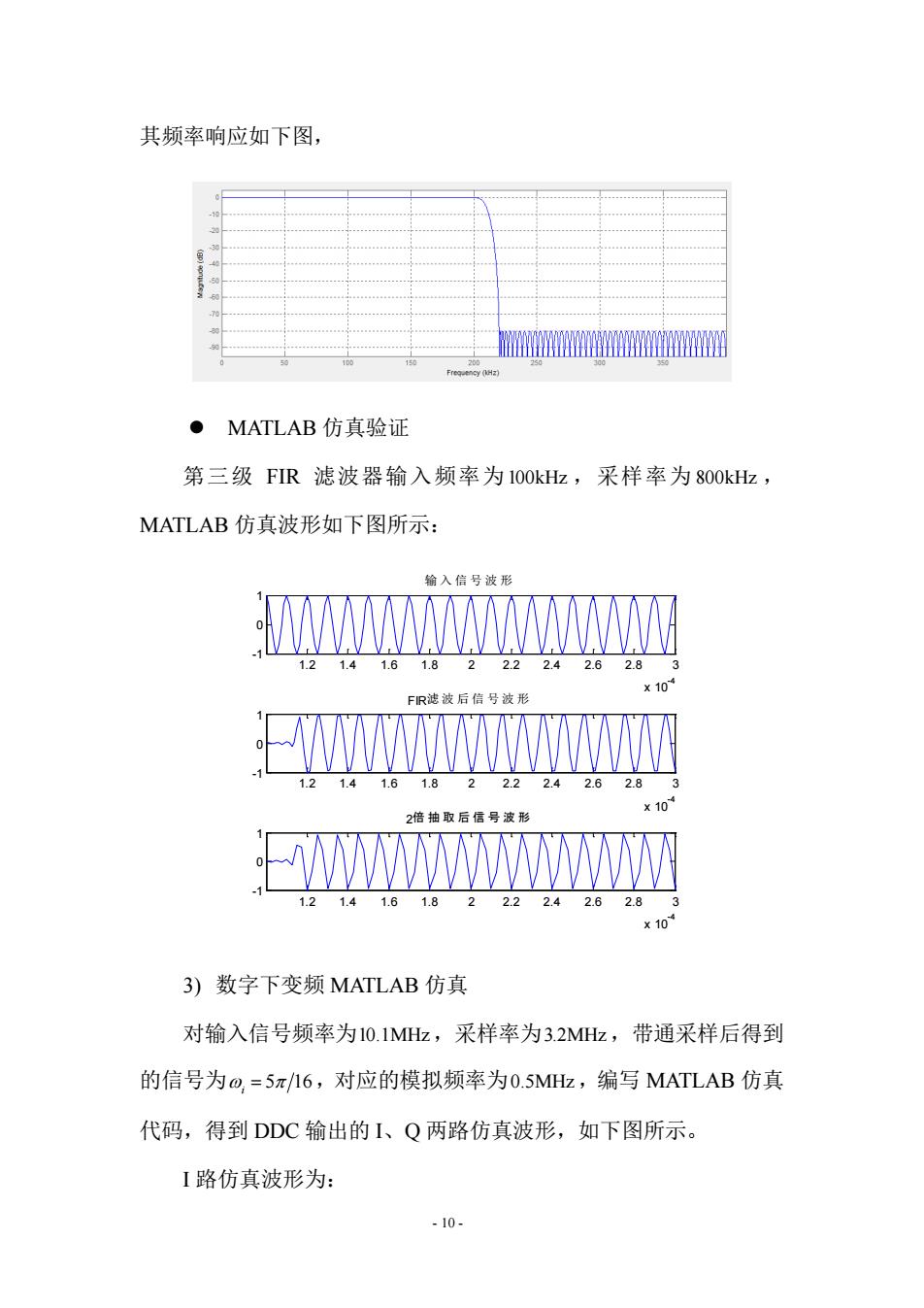
- 10 - 其频率响应如下图, MATLAB 仿真验证 第三级 FIR 滤波器输入频率为100kHz ,采样率为 800kHz , MATLAB 仿真波形如下图所示: 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3 x 10-4 -1 0 1 输入信号波形 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3 x 10-4 -1 0 1 FIR滤波后信号波形 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3 x 10-4 -1 0 1 2倍抽取后信号波形 3) 数字下变频 MATLAB 仿真 对输入信号频率为10.1MHz,采样率为3.2MHz,带通采样后得到 的信号为 5 16 ω π i = ,对应的模拟频率为0.5MHz,编写 MATLAB 仿真 代码,得到 DDC 输出的 I、Q 两路仿真波形,如下图所示。 I 路仿真波形为: