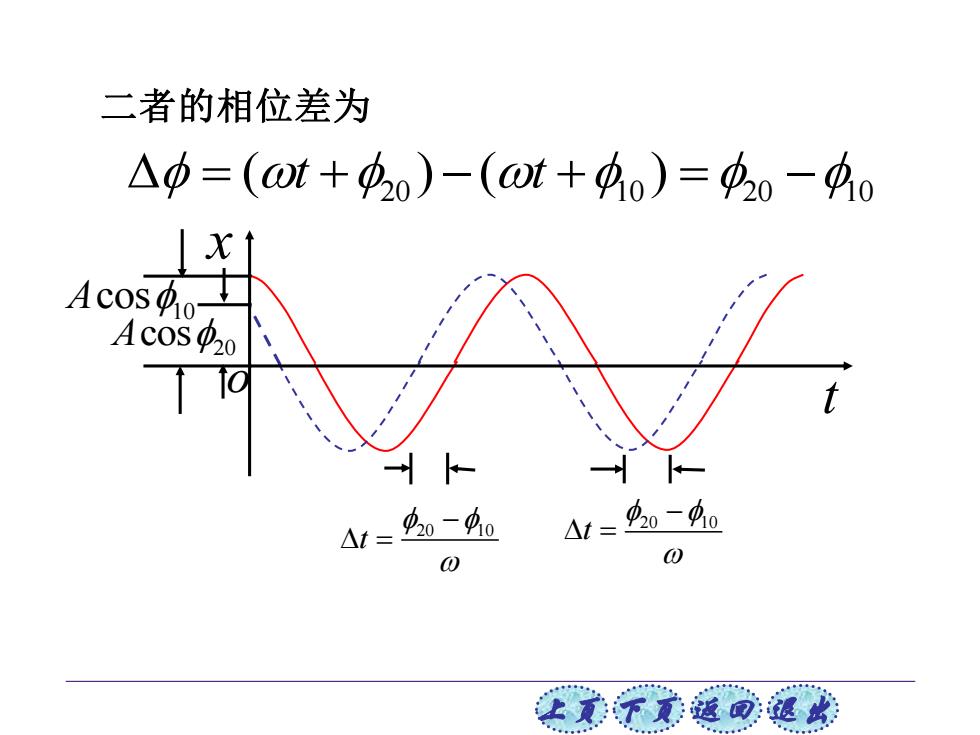
二者的相位差为 △中=(ot+中0)-(ot+中0)=中0-40 Acos Acos20 41=0-4g △1=,-40 0 0 上意不家道可退欢
上页 下页 返回 退出 A/2 x t o 二者的相位差为 20 10 20 10 = + − + = − ( ) ( ) t t 20 10 t − = 20 10 t − = 20 Acos 10 Acos
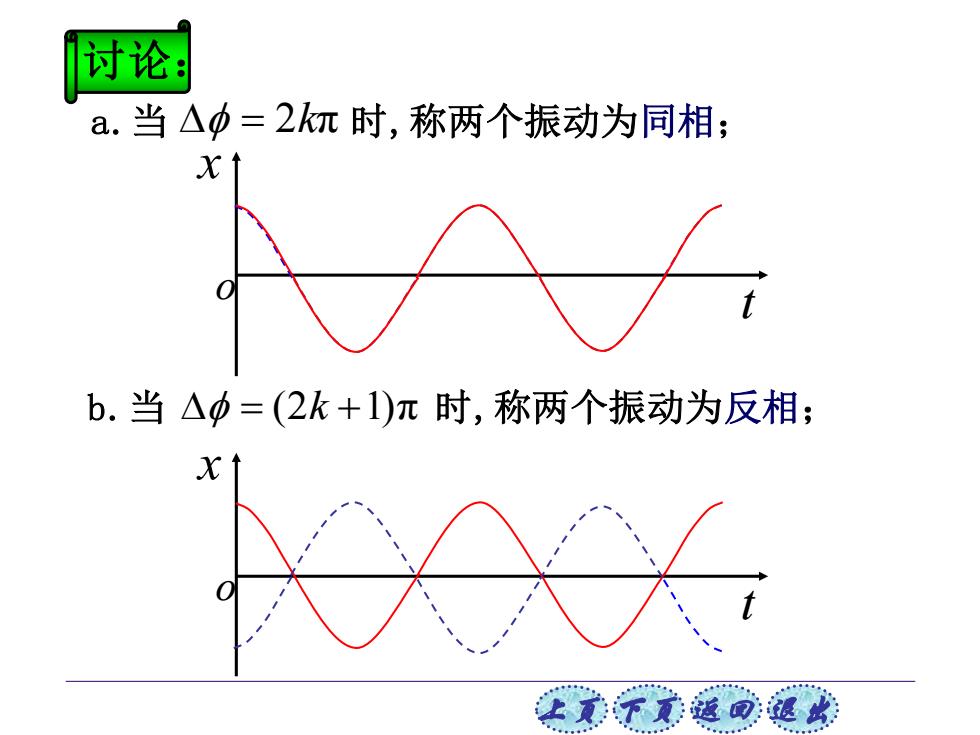
讨论 a.当△中=2k饥时,称两个振动为同相; X↑ b.当△中=(2k+1)π时,称两个振动为反相; X 让美下元返回:退欢
上页 下页 返回 退出 x t o b.当 = + (2 1) k π 时,称两个振动为反相; x t o a.当 = 2kπ 时,称两个振动为同相; 讨论:
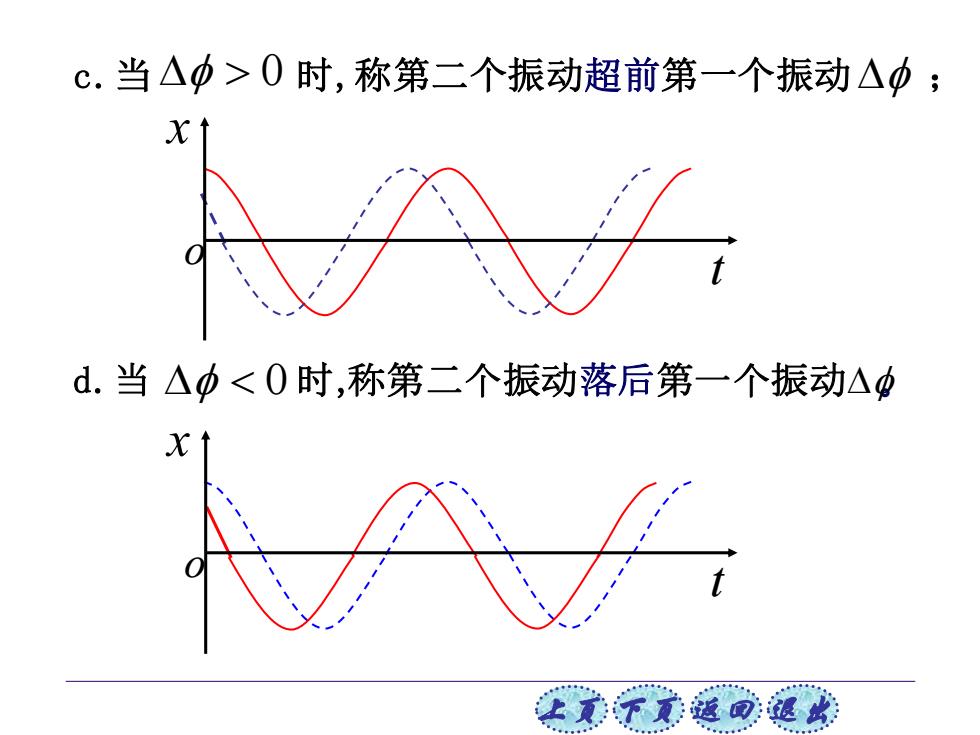
c.当△中>0时,称第二个振动超前第一个振动△中; d.当△中<0时,称第二个振动落后第一个振动△ X 上贰不觉返回退此
上页 下页 返回 退出 d.当 0 时,称第二个振动落后第一个振动 。 x t o x t o c.当 0 时,称第二个振动超前第一个振动 ;

相位可以用来比较不同物理量变化的步调。 对于简谐振动的位移、速度和加速度,存在: x=Acos(at+) v=-Vm sin(at+)=vm cos(ot++/2) a=-am cos(ot+)=a cos(ot+d+) 速度的相位比位移的相位超前π2,加速度的相 位比位移的相位超前元 让美觉返司退
上页 下页 返回 退出 相位可以用来比较不同物理量变化的步调。 对于简谐振动的位移、速度和加速度,存在: 速度的相位比位移的相位超前 ,加速度的相 位比位移的相位超前 。 π 2 π cos( ) = +0 x A t m 0 m 0 v v t v t = − + = + + sin( ) cos( π 2) m 0 m 0 a a t a t = − + = + + cos( ) cos( π)