《普通物理学》课程教学资源（PPT课件）第十一章 机械波和电磁波 11-4 波的能量、波的强度

§11-4波的能量波的强度 弹性波传播到介质中的某处，该处将具有动能和势 能。在波的传播过程中，能量从波源向外传播。 正意子元道回退此

上页 下页 返回 退出 弹性波传播到介质中的某处，该处将具有动能和势 能。在波的传播过程中，能量从波源向外传播。 §11-4 波的能量 波的强度

一、波的能量 考虑介质中的体积△V,其质量为△m(△m=pAV)。当 波动传播到该体积元时，将具有动能△E和弹性势能△E。 平面简谐 支x,)=Acos - 有如下关系： AE-AE,-(AV)sin -9 +40 u 让意文滋可退攻

上页 下页 返回 退出 0 ( , ) cos x y x t A t u       = − +         平面简谐波 2 2 2 0 1 ( )sin 2 x E E A V t u          =  =  − +         k p 有如下关系: 一、波的能量 波动传播到该体积元时，将具有动能 Ek 和弹性势能 Ep 考虑介质中的体积V，其质量为 m(m=V ) 。当

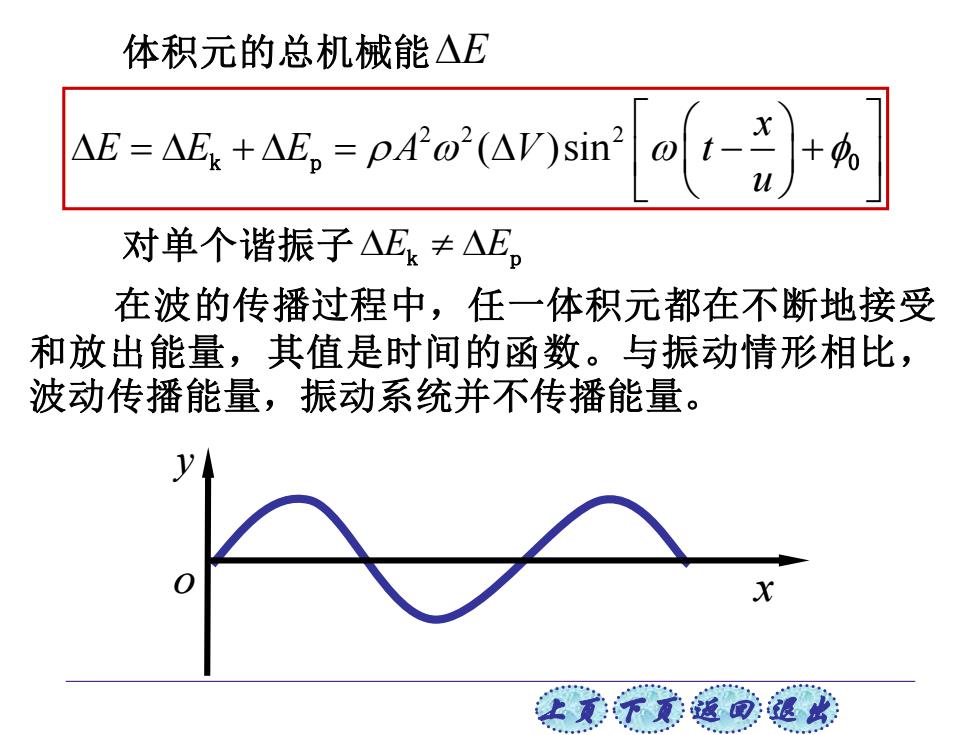
体积元的总机械能△E +NE,-po (AV)sin + 对单个谐振子△E≠△E, 在波的传播过程中，任一体积元都在不断地接受 和放出能量，其值是时间的函数。与振动情形相比， 波动传播能量，振动系统并不传播能量。 让意子意返回退收

上页 下页 返回 退出 对单个谐振子    E E k p 在波的传播过程中，任一体积元都在不断地接受 和放出能量，其值是时间的函数。与振动情形相比， 波动传播能量，振动系统并不传播能量。 体积元的总机械能 E 2 2 2 ( )sin x E E E A V t u          =  +  =  − +         k p 0 y o x

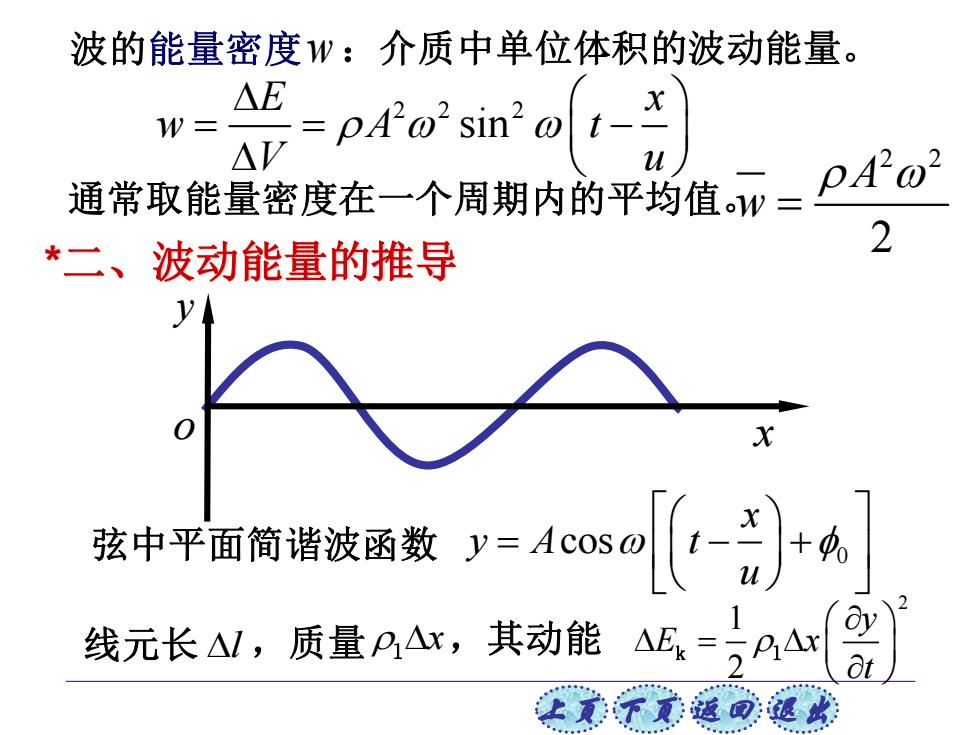
波的能量密度w:介质中单位体积的波动能量。 g=是=p.Pwsiwo到 △E 通常取能量密度在一个周期内的平均值，p=P10 *二、波动能量的推导 2 孩中斗国情谐泼国数ycs0[(+A] 线元长M,质量AA,其动能A=DAr 让美下觉返司速此

上页 下页 返回 退出 *二、波动能量的推导 y o x 弦中平面简谐波函数 0 cos x y A t u       = − +         线元长 l ，质量  x l ，其动能 2 1 2 y E x t      =       k l 2 2 2 sin E x w A t V u       = = −      通常取能量密度在一个周期内的平均值。 2 2 2 A w   = 波的能量密度 w ：介质中单位体积的波动能量

势能 AE,=F(△1-△x) △x很小时 s-ww心-a-定 △x 机械能 2 AF=AEX+AE,=2A (

上页 下页 返回 退出 势能  =  −  E F l x ( ) p x 很小时 1 2 2 2 2 2 1 ( ) ( ) 1 1 2 y y l x y x x x x            =  +  =  +   +                       2 1 2 y E F x x     =       p 2 2 1 1 2 2 y y E E E x F x x x         =  +  =  +            k p l 机械能