[例1]求半径为质量为的均匀圆环,对于沿 直径转轴的转动惯量 解:圆环的质量密度为 n 2元R 在环上取质量元dm,dm 距转轴r dm=d=人Rd0 r=Rcos
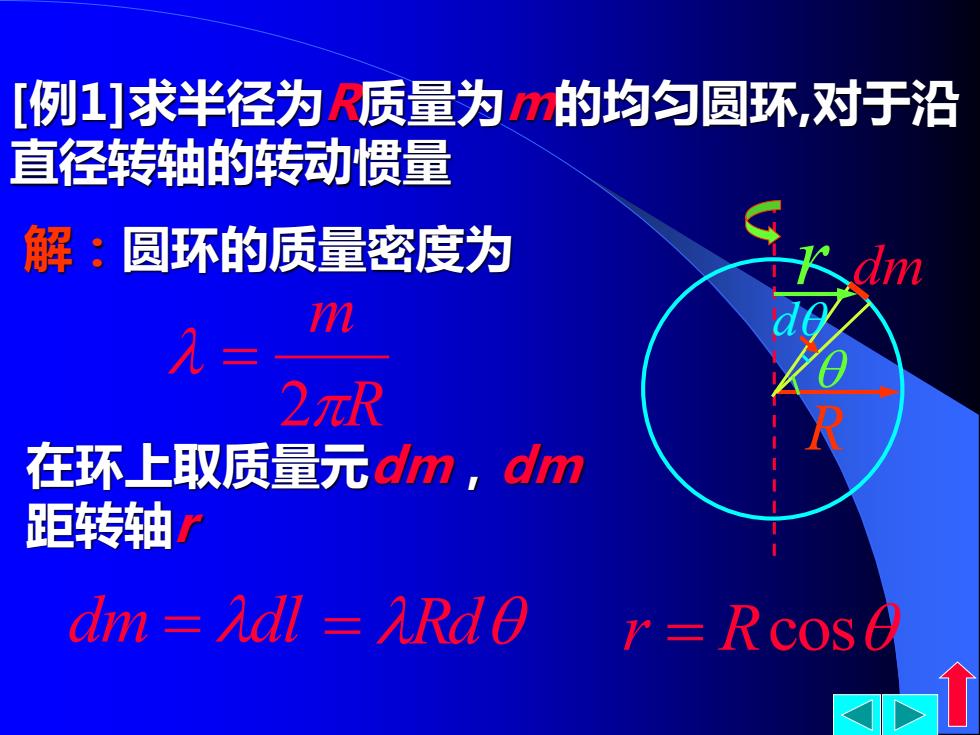
[例1]求半径为R质量为m的均匀圆环,对于沿 直径转轴的转动惯量 R d 解:圆环的质量密度为 r dm R m 2 = 在环上取质量元dm,dm 距转轴r dm = dl = Rd r = Rcos

"dm=2Rcos'0.ARd0 -π/2 =Rπ=mR2 另解 对过环心并与环垂直的转轴 的转动惯量 J:=R'dm=R dm=mR
x y = m J r dm2 − = 2 2 2 2 2 cos R Rd 3 = R 2 2 1 = mR 另解 对过环心并与环垂直的转轴 的转动惯量 = m Jz R dm2 = m R dm 2 2 = mR R

根据对称性有 由垂直轴定理 J.=J=2J = mR2
根据对称性有 x y J = J 由垂直轴定理 z x y J = J + J x = 2J x z J J 2 1 = 2 2 1 = mR

[例2]长/质量的均匀细棒放在xoy平面内 棒与轴成30角,其中心在O点。求它对x y和2轴的转动惯量 解:细棒质量密度为 A=m 在棒上取长为d的质量元 ".dy dl sin O dx dl cos0 dm Adl
[例2]长l、质量m的均匀细棒放在xoy平面内, 棒与x轴成300角,其中心在O点。求它对x、 y和z轴的转动惯量 dl y o 30 x y z 解:细棒质量密度为 = m l 在棒上取长为dl的质量元 dy = dlsin dx = dl cos dm = dl