
二、导纳 1、定义 U 当名-后4g-r 导纳模|Y|=I/U 导纳角py=必,-业u 导纳Y的代数形式可写为 Y=G+iB 其实部为电导,虚部为电纳。 例:Z=3+i4 Y=3/25-j4/25 =1/3+j1/4×
二、导纳 1、定义 def I Y U = = ( ) i u I U − = Y Y 导纳模 | Y | = I / U 导纳角 Y = i − u 导纳Y的代数形式可写为 Y= G + jB 其实部为电导,虚部为电纳。 例: Z=3+j4 Y=1/3 + j1/4× Y = 3/25 – j 4/25 N0 + - U I

2、单个元件R、L、C的导纳 -G=1 R 1 YL= joL =-J Y=joC 3、感纳和容纳 感纳品 容纳B。=DC
2、单个元件R、L、C 的导纳 R YR G 1 = = 1 1 j j YL L L = = − j Y C C = 3、感纳和容纳 感纳 1 BL L = 容纳 BC =C

四、欧姆定律的相量形式 由以上可见,引出了Z、Y参数后,对于正弦稳态电 路中的任一不含独立源的二端网络(含单个R、L、C 元件),其端口的VAR的相量形式可归纳为统一形式 U-zi i-YU 这两个式子常称为欧姆定律的相量形式,在正弦稳 态电路的分析中是十分有用的
四、欧姆定律的相量形式 由以上可见,引出了Z、Y参数后,对于正弦稳态电 路中的任一不含独立源的二端网络(含单个R、L、C 元件),其端口的VAR的相量形式可归纳为统一形式 这两个式子常称为欧姆定律的相量形式,在正弦稳 态电路的分析中是十分有用的
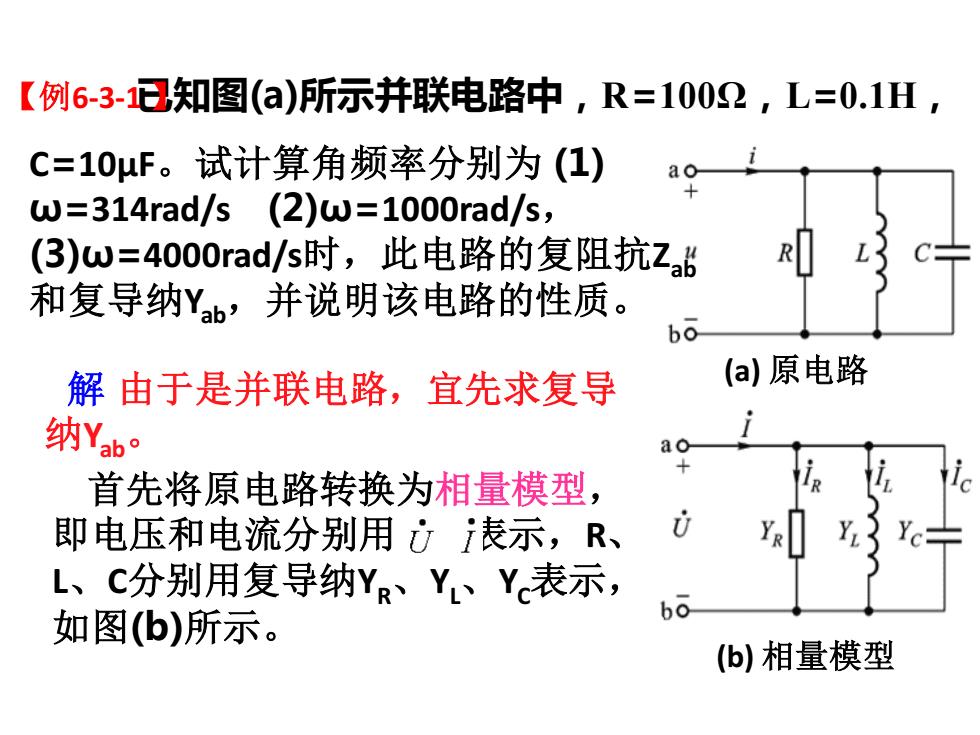
【例6-3-1日知图()所示并联电路中,R=1002,L=0.1H, C=10μF。试计算角频率分别为(1) ao w=314rad/s(2)w=1000rad/s, (3)w=4000rad/s时,此电路的复阻抗Z6 R 和复导纳Yb,并说明该电路的性质。 bo 解由于是并联电路,宜先求复导 (a)原电路 纳Yab· 首先将原电路转换为相量模型, 即电压和电流分别用)表示,R、 L、C分别用复导纳YR、Y、Y表示, 如图(b)所示。 bo (b)相量模型
已知图(a)所示并联电路中,R=100Ω,L=0.1H, (a) 原电路 (b) 相量模型 解 由于是并联电路,宜先求复导 纳Yab。 首先将原电路转换为相量模型, 即电压和电流分别用 、 表示,R、 L、C分别用复导纳YR、YL、YC表示, 如图(b)所示。 C=10µF。试计算角频率分别为 (1) ω=314rad/s (2)ω=1000rad/s, (3)ω=4000rad/s时,此电路的复阻抗Zab 和复导纳Yab,并说明该电路的性质。 【例6-3-1 】

根据复导纳定义式可得 -1 ao 五=1 Y Yc= F-j@C 则 =0=R bo (b)相量模型 ic=YaU=j@CU 根据歌CL的相量形式得 i=2+i+远=(R+j+ioc0 由复导纳定义式得 =上+:+joO R
根据复导纳定义式可得 (b) 相量模型 则 根据KCL的相量形式得 由复导纳定义式得