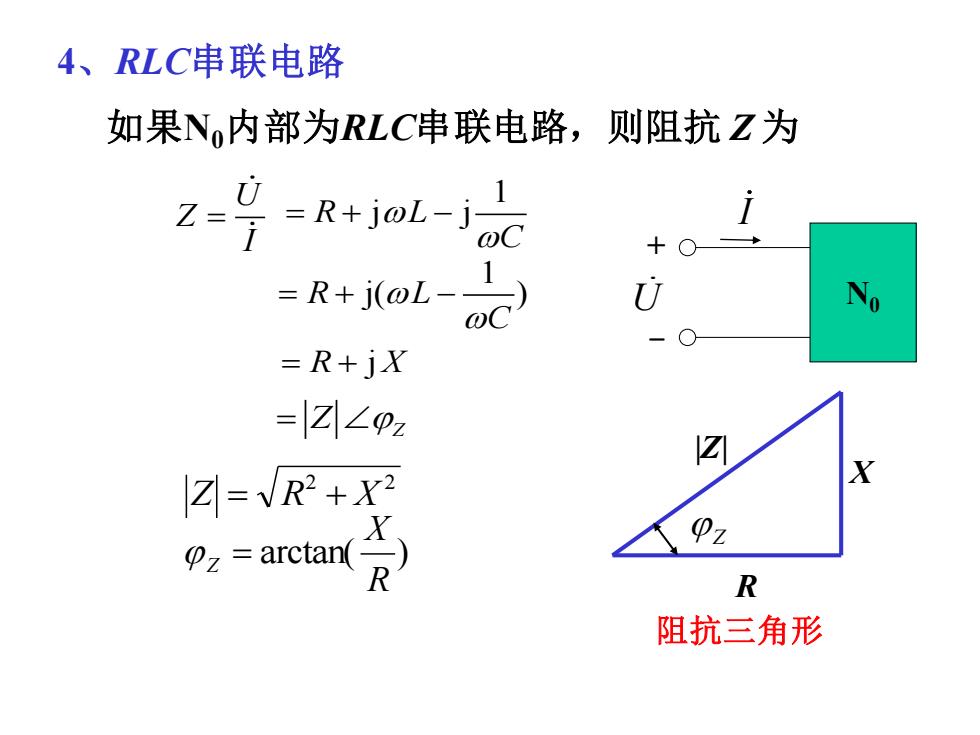
4、RLC串联电路 如果N内部为RLC串联电路,则阻抗Z为 Rjol-idc ?oy =R+j(@L- U =R+jx =|Z∠pz Z=VR2+x2 X R 阻抗三角形
4、RLC串联电路 如果N0内部为RLC串联电路,则阻抗 Z 为 U Z I = 1 R L j j C = + − 1 R L j( ) C = + − = + R Xj = Z Z 2 2 Z = R + X arctan( ) R X Z = R X |Z| Z 阻抗三角形 N0 + - U I

电路的性质Z=R+j(oL- )=R+jx X pz=arctan(R) 当wL>1/wC,X>0,p>0, 电压u超前电流i,称Z呈感性; 当wL<1/wC,X<0,p<0, 电压u落后电流i,称Z呈容性; 当wL=1/wC,X=0,0=0, 电压和电流i同相,称Z呈电阻性 电路性质由什么决定? ω一定时,电路性质由元件参数决定
当ωL > 1/ωC ,X > 0,φ>0, 电压 u 超前电流 i,称 Z 呈感性; 当ωL < 1/ωC ,X < 0,φ<0, 电压 u 落后电流 i,称 Z 呈容性; 当ωL = 1/ωC ,X = 0,φ=0, 电压 u 和电流 i 同相,称 Z 呈电阻性 电路的性质 电路性质由什么决定? ω 一定时,电路性质由元件参数决定 1 Z R L R X j( ) j C = + − = + arctan( ) R X Z =

电路的性质 Z=R+oL-2)=R+jW Pz arctan( 假设R、L、C已定,电路性质能否确定? 不能!! 当ω不同时,可能出现: X>0,或X<0,或X=0
电路的性质 假设R、L、C已定,电路性质能否确定? 不能!!! 当ω不同时,可能出现: X > 0,或 X < 0 , 或X = 0 1 Z R L R X j( ) j C = + − = + arctan( ) R X Z =
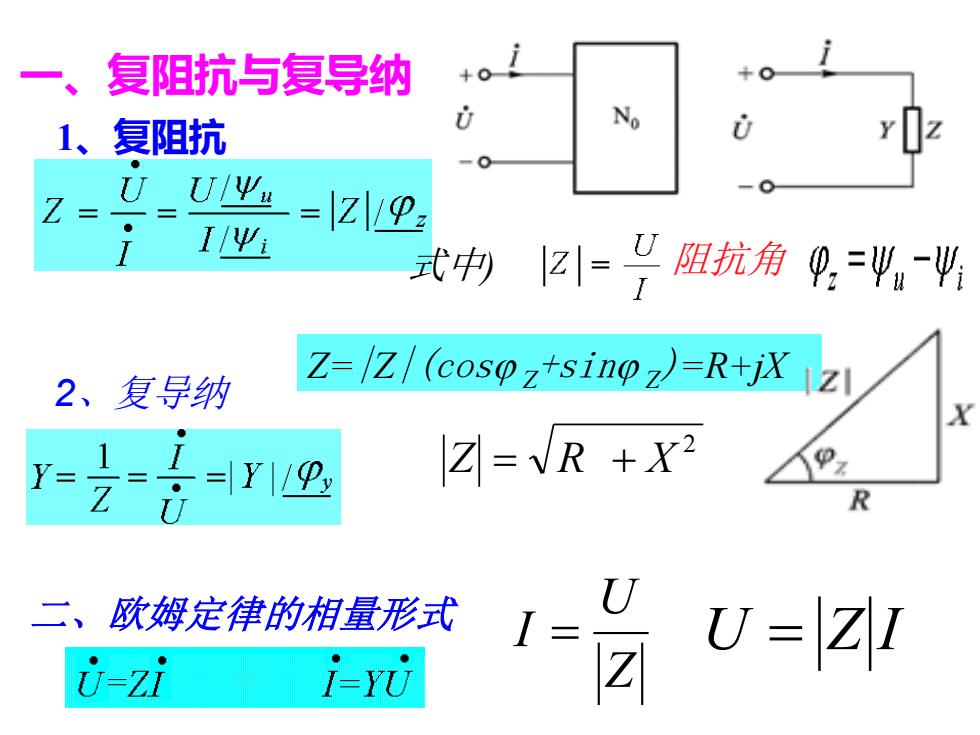
复阻抗与复导纳 1、复阻抗 N Z= UU/Ψ4 =zliP: I/Ψ 式中 2川=可阻抗角月,=业4 2、复导纳 Z-/Z/(cosoz+sinpz)=R+iXz X 1 -=YI Z=VR+x2 U R 二、欧姆定律的相量形式 I= U-zi i-YU U=ZI
《电路分析简明教程》 一、复阻抗与复导纳 1、复阻抗 式中) 阻抗角 2、复导纳 Z U I = U = Z I Z=|Z|(cos Z +sin Z )=R+jX 2 Z = R + X 二、欧姆定律的相量形式
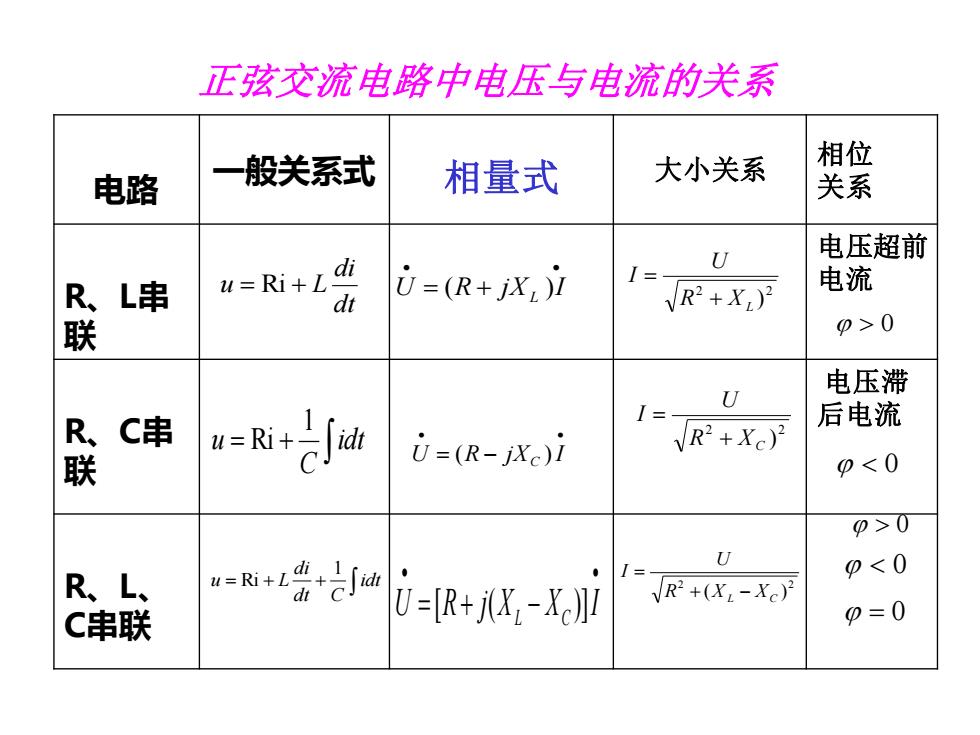
正弦交流电路中电压与电流的关系 相位 电路 一般关系式 相量式 大小关系 关系 U 电压超前 u=Ri+L U=(R+jX,)立 I= 、L串 R2+X) 电流 联 p>0 电压滞 u+之过 U R、C串 后电流 VR2+Xc) 联 U=(R-jXe)i p<0 p>0 U p<0 R、L、 VR+(X:-Xc) C串联 U=[R+j(X-Xc)I p=0
正弦交流电路中电压与电流的关系 电路 一般关系式 相量式 大小关系 相位 关系 R、L串 联 电压超前 电流 R、C串 联 电压滞 后电流 R、L、 C串联 dt di u = Ri + L = + idt C u 1 Ri • • U = R + jX I L ( ) [ ( )] U R j X X I L C • • = + − • • U = R − jX I C ( ) = + + idt dt C di u L 1 Ri 0 0 2 2 ( ) R XL X C U I + − = 2 2 ) R XL U I + = 2 2 ) R X C U I + = 0 0 = 0