
下面依据不同的w分别计算如下: (1)w=314rad/5时 100+j314×0.1+j314×10×10s=0.01-j0.0287S 1 则 Zo= 1 1 70.01-j0.028 2=(10.8+j31.1)2 由于B<0(X>0),故此并联电路在w=314rad/s时 呈电感性。 2)w=1000rad/5时 %-(10+100×0i +j1000×10×10-)S=0.01S 赠于0X0,置e并联电路在w=10o0orad/s 时呈电阻性
下面依据不同的ω分别计算如下: 则 由于B<0(X>0),故此并联电路在ω=314rad/s时 呈电感性。 (2)ω=1000rad/s时 由于B=0(X=0),故此并联电路在ω=1000rad/s 时呈电阻性。 则 (1)ω=314rad/s时

(3)o=4000rad/s时 1 星s0054000x27 ,+j4000×10×10)S=(0.01+j0.0375)S 则 Y0.01+j0.03752=(6.64-j24.9)2 1 由于B>0(X<0),故此并联电路在ω=4000rad/s 时呈电容性。 ◆由本例题可知,一般情况下,复阻抗、复导纳是角 频率的函数,同一个电路在不同的频率下所呈现的复 阻抗、复导纳是不同的,并且电路的性质也会发生变 化。所以对于一个实际电路,在不同的频率下有不同 的等效电路,它的复阻抗、复导纳都是针对某一特定 频率的
(3)ω=4000rad/s时 则 ◆由本例题可知,一般情况下,复阻抗、复导纳是角 频率的函数,同一个电路在不同的频率下所呈现的复 阻抗、复导纳是不同的,并且电路的性质也会发生变 化。所以对于一个实际电路,在不同的频率下有不同 的等效电路,它的复阻抗、复导纳都是针对某一特定 频率的。 由于B>0(X<0),故此并联电路在ω=4000rad/s 时呈电容性

§6-4正弦稳态电路的相量分析法 在用相量法分析计算时,引入正弦量的相量、 阻抗、导纳和KCL、KVL的相量形式,它们在形 式上与线性电阻电路相似。 1∑i=0 Σu=0 对于电阻电路有: l u=Ri i=Gu Σ1=0 ΣU=0 对于正弦电流电路有: U=zi 1=YU
§6-4 正弦稳态电路的相量分析法 在用相量法分析计算时,引入正弦量的相量、 阻抗、导纳和KCL、KVL的相量形式,它们在形 式上与线性电阻电路相似。 i = 0 u = 0 = 0 • I = 0 • U u = Ri i =Gu • • U = Z I • • I = Y U 对于电阻电路有: 对于正弦电流电路有:

用相量法分析时,线性电阻电路的各种分析 方法和电路定理可推广用于线性电路的正弦稳态 分析。 差别仅在于所得电路方程为以相量形式表示 的代数方程以及用相量形式描述的电路定理,而 计算则为复数运算
用相量法分析时,线性电阻电路的各种分析 方法和电路定理可推广用于线性电路的正弦稳态 分析。 差别仅在于所得电路方程为以相量形式表示 的代数方程以及用相量形式描述的电路定理,而 计算则为复数运算
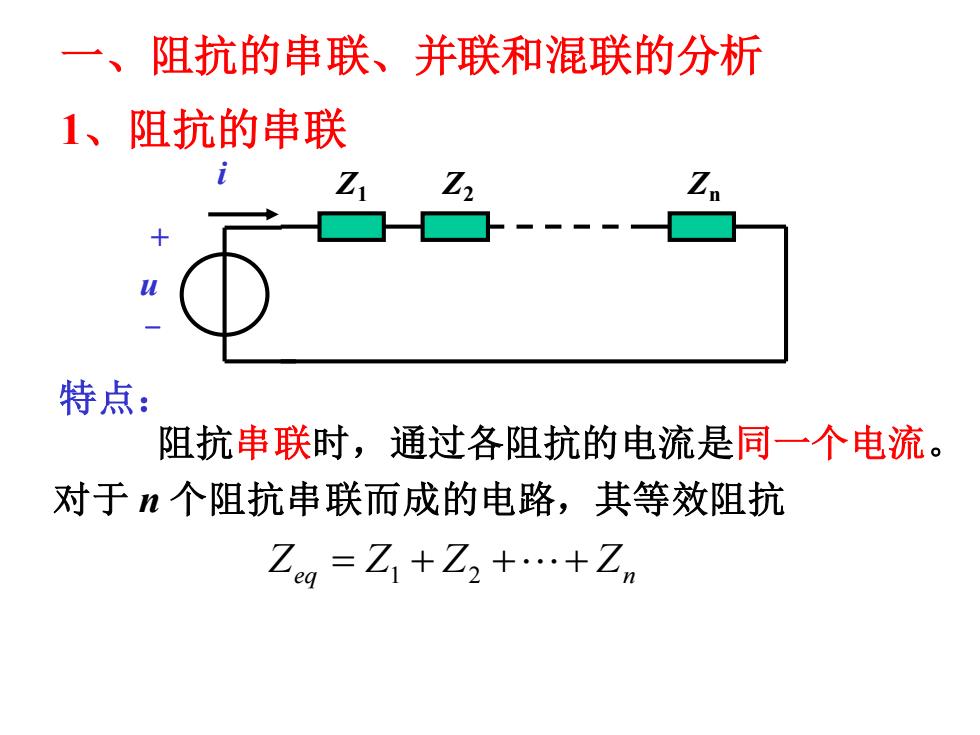
一、阻抗的串联、并联和混联的分析 1、阻抗的串联 Z Z 特点: 阻抗串联时,通过各阻抗的电流是同一个电流。 对于n个阻抗串联而成的电路,其等效阻抗 Zg=Z1+Z2+.+Zm
一、阻抗的串联、并联和混联的分析 Zeq Z Z + Zn = + + 1 2 特点: 阻抗串联时,通过各阻抗的电流是同一个电流。 + - u i Z1 Z2 Zn 对于 n 个阻抗串联而成的电路,其等效阻抗 1、阻抗的串联