
1.正态总体平均数的假设测验 (1)单个样本平均数的假设测验 解:第一步提出假设: Ho:μ≥100HA:4p100 第二步确定显著水平0=0.05 第三步计算概率 u=4=4-93-100-8 5 72 Vn V64 第四步推断

单尾与双尾测验比较 相同点: (1)两种测验的测验步骤相同。 (2)在单个样本平均数、两个样本平均数相比较的假设测验中都可应用。 (3)都可应用u测验或t测验。 不同点: (1)假设的形式略有不同。 两尾:Ho:μ=o:Ha:μ≠u0 H0:μ1=μ2:Ha:μ1≠μ2 一尾:左尾:Ho:μ≥oHa:μ<0 Ho:μ1≥μ2;Ha:μ1<μ2 右尾:Ho:μ≤o:Ha:u>μ0 Ho:μ1≤μ2:Ha:μ1>μ2 (2)查u表或表时a值有差异:两尾测验可直接用显著水平a查两尾U 值表示或t值表;一尾测验则需用2ā查两尾u值表或值表
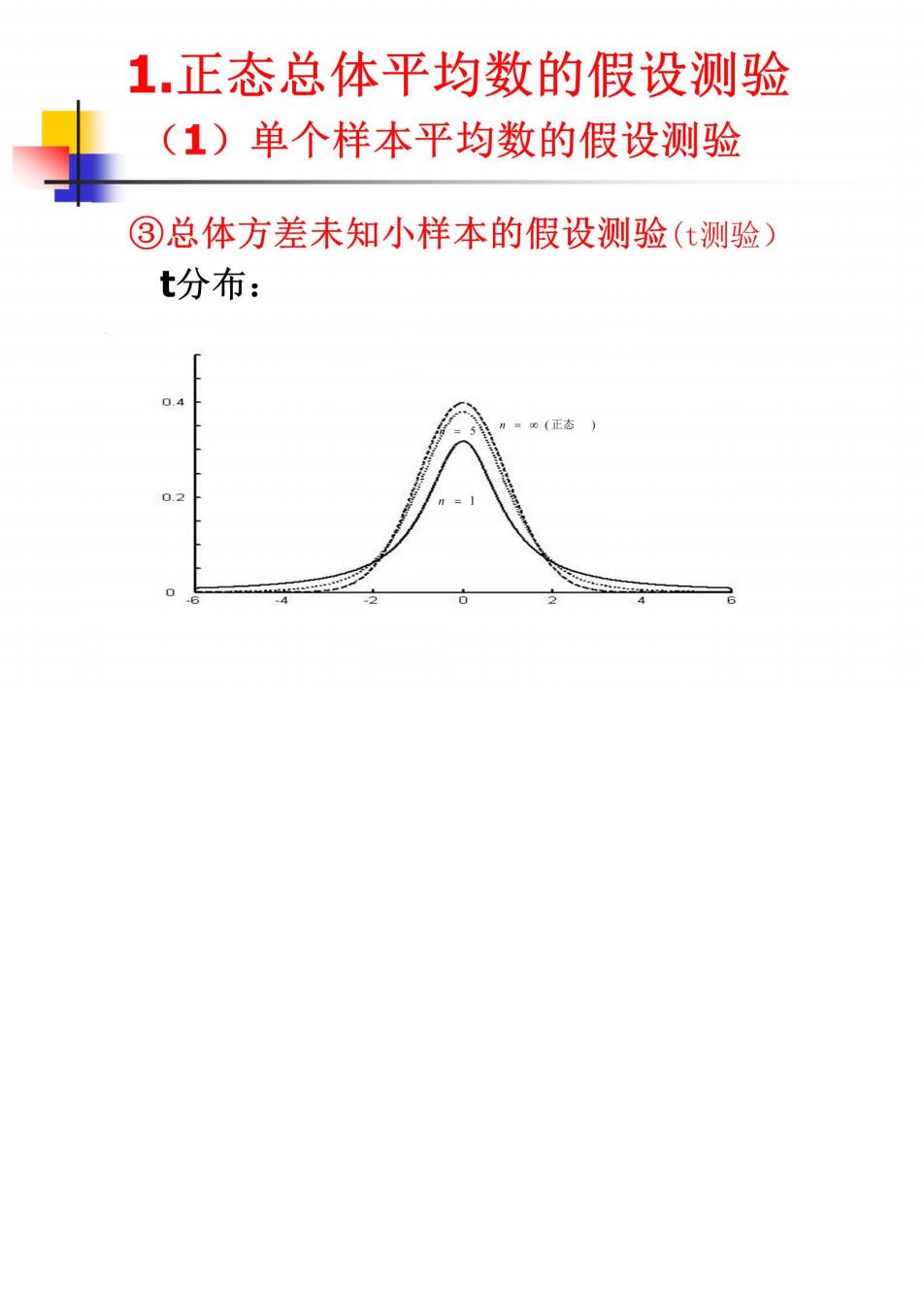
1.正态总体平均数的假设测验 (1)单个样本平均数的假设测验 ③总体方差未知小样本的假设测验(t测验) t分布: :(正态

1.正态总体平均数的假设测验 (1)单个样本平均数的假设测验 t测验: 【例3】某小麦良种的千粒重μo=35.5g。现从外地引 入一高产品种,在8个小区种植,得千粒重(g): 35.6、37.6、33.4、35.1、32.7、36.8、35.9、 34.6。问新引入品种的千粒重与当地品种有无显著差 异(a=0.05)?

1.正态总体平均数的假设测验 (1)单个样本平均数的假设测验 解:第一步提出假设:Ho:4=35.5;Ha:u≠35.5 第二步确定显著水平a=0.05 第三步计算概率 x=(35.6+37.6+K+34.6)/8=35.2 SS=35.62+37.62+L+34.62-(281.7)2/8=18.83 s2=18.83/8-1=2.69 t=4=X'=35.2-355-0.517 s22.69 Vn V 8 第四步推断t05.7=2.365