
第4卷第1期 扬州大学学报(自然科学板) Vol.4 No.1 2001年2月 JOURNAL OF YANGZHOU UNIVERSITY (NATURAL SCIENCE EDITION) Feb.2001 重抽样技术一自举法 草核 (场州大学数量速传研究,扬州225009) 德要,自举法是在1个容意为的原始样本中重复抽取一系列容量也是:的随机样本,并保证每次抽样 中每一样本观察值被热取的概率都是1/(复置抽样).这种方法可用来检查样本统计数©的基本性质,估 计0的标准误和确定一定置信系较下日的置信区间。提出单变量白举、多变量自举和离回归自举3件方 法,并各附实例。包简要地讨论了重抽样的另一种技术一白析法 关罐词。置轴样:单变量自举:多变黄自举;离回归自举 中困法分黄号:0212.2 文献标识码:A 文章编号:1007-824X(2001)01-0001-05 1意义 自举法是对1个样本资料进行复置抽样以产生一系列“新”的样本的一种方法,也是现代统计学 研究中应用领域极广的一种重抽样技术. 设某总体具有参数日=(@)(《=1,2,…,p);现从中抽得1个容量为的随机样本,其观察值为Y) (j=1,2,,根据Y,经过一定途径(此途径可以有明确的表达公式,也可以没有:可简也可繁)可 得到估计数=(⑧).现在要间:①这种估计的途径是否有效?或者说A是否是的无偏估计?② a的分布如何?或者说a的标准误(即月分布的标准差)及其对于日的100(1一a)%置信区间是什么? 这些同题,当估计数A及a的标准误不能直接从理论导出(即不能给出其数学期望)、a的分布为未 知时(例如许多非线性统计数或表型相关系数、传相关系数等),或者要把某一样本结果与一定理论 假设下的总体结果比较时(例如多正态混合分布下完全棋型和缩简模型的似然比测验),将显得特别 重要。自举法是近年发展起来的解决上述问题的一种较为有效的方法.它是从1个样本的资料 产生“新"的能够代表被研究总体的多个样本,从面模拟出A的分布,并得到其平均数和标准差。依赖 于电子计算机的大容量和高效率,自举抽样程序已非常容易实现四 本文提出的是自举拍样的3种具体方法。 2 单变量自举 2.1方法 设1个样本具变量Y,Y,…,Y,用某种方法得到其对总体参数A的估计值则在抽样时,每 一轮都要从这n个变量中抽取1个容量也是性的随机样本,并保证每一变量在每轮每次抽样中的枝 抽取概率都是1/(相当于经典方法的复置抽样).此过程一般可用随机数表或由计算机输出个 0一1之间的随机数实现。即:先将样本变量编码为1,2,…,n;然后取分组距离1/m将区间[0,1]分成 个互斥的分隔: 收孩日期:2000-11-08 着金项日,四索自然科学蓄金实助项目(3967031) 万方数据
第4卷第1期 2001年2月 扬州大学学报(自然科学版) JoURNAL OF YANGzHOU UNIVERSITY(NATURAL SCIENCE EDITIoN) V01.4 No.1 Feb.200I 重抽样技术——自举法 莫惠栋 (扬州大学数量遗传研究室.扬州225009) 摘要;自举法是在1个容量为”的原始样本中重复抽取一系列容量也是n的随机样本,并保证每次抽样 中每一样本观察值被抽取的概率都是l向(复置抽样).这种方法可用来检查样本统计效a的基本性质,估 计扫的标准误和确定一定置信系歙下乎的置信区间.提出单变量自举、多变量自举和离回归自举3种方 法,并各附实倒.也简要地讨论了重抽样的另一种技术——自析法. 美麓词t重抽样,单变量自举;多变量自举;离回归自举 中圉法分类号t O 212.2 文献标识码:A 文章编号;1007—824x(2001)ol—000l—06 1意义 自举法是对1个样本资料进行复置抽样以产生一系列“新”的样本的一种方法,也是现代统计学 研究中应用领域极广的一种重抽样技术. 设某总体具有参数日;(B)“;1,2,…,p);现从中抽得1个容量为n的随机样本,其观察值为L (J=1,2’..·,一);根据n,经过一定途径(此途径可以有明确的表达公式,也可以没有}可简也可繁)可 得到估计数0一(斑).现在要问:①这种估计聃的途径是否有效?或者说晚是否是只的无偏估计?② 鼠的分布如何?或者说良的标准误(即鼠分布的标准差)及其对于馥的100(1一a)%置信区间是什么? 这些同题,当估计数晚及反的标准误不能直接从理论导出(即不能给出其数学期望)、岛的分布为未 知时(例如许多非线性统计数或表型相关系数、遗传相关系数等),或者要把某一样本结果与一定理论 假设下的总体结果比较时(例如多正态混合分布下完全模型和缩简模型的似然比测验),将显得特别 重要.自举法是近年发展起来的解决上述问题的一种较为有效的方法““].它是从1个样本的资料 产生“新”的能够代表被研究总体的多个样本,从而模拟出鼠的分布,并得到其平均数和标准差.依赖 于电子计算机的大容量和高效率,自举抽样程序已非常容易实现…. 本文提出的是自举抽样的3种具体方法. 。 2单变量自举 2.1方法 设1个样本具变量y。,y∥一,y-,用某种方法得到其对总体参数岛的估计值巍.则在抽样时,每 一轮都要从这”个变量中抽取1个容量也是n的随机样本,并保证每一变量在每轮每次抽样中的被 抽取概率都是1向(相当于经典方法的复景抽样).此过程一般可用随机数表[53或由计算机输出n个 o~1之间的随机数实现.即:先将样本变量编码为1,2,…,n;然后取分组距离1向将区间[o,1]分成 n个互斥的分隔: 收稿日期t 2000一11一08 基盒项目:国家自然科学基金资助项目(39670391) 万方数据

2 扬州大学学(白然科学版】 第4整 (1) 出现的随机数,凡在0一子(低限用≤号,高限用<号,即0≤R<,下同)之间的取编码“1“变量,凡 在一异之间的取编码“2变量,,凡在号一1之间的取编网变量,这就称为自举抽样,由这。 个“新”变量组的样本则称为自举样本(即mple.当对原始样本变基重复进行,m轮自举袖 样,就得到m个容量均为n的自举样本。再对每一样本都按照在原始样本中所用的计求d的方法,求 其统计数高,得到1个次数为m的高分布.这称为自举统计数成分布.由此分布,我们就可以研究A 的基本性质,其最主要特征数是自举平均数:(boostrap average)和自举标准误,(tdard error),定义为: 0:-8u/m, (2) =[∑(0.-0/(m-10] (3) 以上(3)式即总分布的标准差。不论成是什么样的统计数,自举抽样都能意健地提供它的平均数和标 准误估计.这是自举法的一个重要特征和丰凡功能. 如果A能够描述有关随机变量的取值中心(即通常所说的“无偏估计”),则品和日:之间的差异应 在误差(标准误)所许可的范围内:如果的标准误为未知,则5戏将是其最佳替代。一殷为估计8;和 ,m-100即可(这是在0和5能相对稳定的意义上而言的),不必大于200.但是,如果要了解成的 较精确分布和对于8的100(1一a)%置信区间,一般应选m=1000.这时,在值从小到大的顺序排 列中,k=6,26和51的成值依次为对于日的置信系数为99%,95%和90%的区间低限;而=995, 975和950的高值则依次为相应的区间高限.它们与高的分布形状(如是否左右对称)无关 2.2示例 10位因食用沙门氏菌污染食物而“中毒”的患者的潜伏期(⑧/小)列于表1列2.计算的统计数有 潜伏期的算术平均数A,标准差a,日的标准误月,A的标准误A.由于已知潜伏期资料多属左偏分 布),故又计算中位数A(在偏态下以中位数描述变量中心常较算术平均数更为恰当,因为一组变量 与其中位数离差的绝对值之和不大 们与任何其他统计数离差的绝对值之和).其定义和结果为: 8==2Y/m=260/10=26h, 0,=s=[∑Y,-/m-1)]-18.5h, (4) 8=5=/√=18.5/o=5.85h, 0=5.=5//2m=18.5//20=4.14h, a=Md=(Y,+Y,/2=(20+22)/2=21h. 以上成和日是假设Y,的分布为正态的结果;A中的Y和Y。是Y,从小到大顺序排列时=5和6的 此例”=10,故根据(1)式,自举随机号的分组数列为00.1一0.2~0.3一0.4一0.5一0.6~0.7 0.8~0.91.0. 其第1 3 单本及其根据于(4)式的计算结果均列于表1.经100次自举抽样 后,各自举统计数的变幅及根据(2)或(3)式算得的平均数、标准误则列于表2.表1和表2的结果主 要说明: 1)石(表2)和a,(表1)都有一定差异,但其最大差异都在土0.5个标准误范固内.例如对于y是 (26.0-25.01)/4.77-0.208,对于s是(18.5-16.46)/4.83=0.422.这表明不能否认各个A都是无 万方数据
2 扬州大学学报(自然科学敝) 第4卷 o~上,上~呈,呈~立,…,竺1~1' (1) n n 月 n ” ” 出现的随机数,凡在o~寺(低限用≤号,高限用<号,即o≤R<寺;下同)之间的取编码“l”变量,凡 在音~音之间的取编码“2”变量,…,凡在!≠~1之间的取编码“””变量·这就称为自举抽样,由这n 个“新”变量组成的样本则称为自举样本(bo。tstrap sample).当对原始样本变量重复进行m轮自举抽 样,就得到m个容量均为”的自举样本.再对每一样本都按照在原始样本中所用的计求鼠的方法,求 其统计数鼠,得到1个次数为m的巍分布.这称为自举统计数群分布.由此分布,我们就可以研究穗 的基本性质,其最主要特征数是自举平均数目:(b00strap ave。age)和自举标准误叫(boostmp standard error),定义为: 口:=>:a:加, (2) 置 蹦一『∑(a:一口:)2/(m一1)]“2. (3) 。鬲 。 以上(3)式即劈分布的标准差.不论嶷是什么样的统计数,白举抽样都能稳链地提供它的平均效和标 准误估计.这是自举法的一个重要特征和非凡功能. 如果鼠能够描述有关随机变量的取值中心(即通常所说的“无偏估计”),则岔和口:之间的差异应 在误差(标准误)所许可的范围内i如果窟的标准误为未知,则州将是其最佳替代.一般为估计a:和 轼,m;100即可(这是在口:和蹦能相对稳定的意义上而言的),不必大于200.但是,如果要了解毹的 较精确分布和对于鼠的100(1一n)%置信区间,一般应选m一1 000.这时,在以值从小到大的顺序排 列中,j=6,26和51的以值依次为对于豌的置信系数为99%,95%和90%的区间低限;而{=995, 975和950的靠值则依次为相应的区间高限.它们与巍的分布形状(如是否左右对称)无关. 2.2示倒 lo位因食用沙门氏菌污染食物而“中毒”的患者的潜伏期(反/h)列于表1列2.计算的统计数有: 潜伏期的算术平均数目。,标准差巩,鱼的标准误吼,巩的标准误鼠.由于已知潜伏期资料多属左偏分 布‘”,故又计算中位数兜(在偏态下以中位数描述变量中心常较算术平均数更为恰当,因为一组变量 与其中位数离差的绝对值之和不大于它们与任何其他统计数离差的绝对值之和).其定义和结果为: 口。;予;∑一加一260/10=26 h, l 目。=s一[∑(L一,)2/h一1)]”一18.5 h, I 以=曲一s//i一18.5//而=5.85 h, 良;L—s//磊一18.5//丽一4.14 h, 兜=Md一(y;+y。)/2=(20+22)/2—21 h. (4) 以上巩和吼是假设n的分布为正态的结果;吼中的ys和ye是L从小到大顺序排列时J=5和6的 变量. 此例n一10,故根据(1)式,自举随机号的分组数列为o~o.1~o.2~o.3~o.4~o.5~o.6~o.7 ~o.8~o.9~1.o.其第1~3自举样本及其根据于(4)式的计算结果均列于表1.经100次自举抽样 后,各自举统计数的变幅及根据(z)或(3)式算得的平均数、标准误则列于表2.表l和表2的结果主 要说明: 1)a:(表2)和鼠(表1)都有一定差异,但其最大差异都在士o.5个标准误范围内.例如对于,是 (26.o一25.01)/4.77一o.208,对于s是(18.5一16.46)/4.83=o.422.这表明不能否认各个岔都是无 万方数据

第1期 莫惠株:重抽样技术一自举法 3 表110例沙门氏葡食物中海患者的港伏期(风/h)和3个自举样本 Table 1 Incubation period (/h)of 10 sufferers from Salmomella and 3 bootstrap samples 第1个自华洋本 变量9 第2个自举件本 第3个自举样本 随机号变量号变量Y,随机号变量号变量出,随机号变号变量Y, 25 9 13 29 9 623 23 0.239 96 10 3 8m 5 -5 52动 偏估计数。 2)3个样本平均数的标准误(,)来自各不 表2表1资料自¥抽样各统计数的 平均数和标准误(m一100》 相同的定义:5,85是基于观寒样本随机抽自正 of100 态总体的假设47 是自举样本平均数分布 h 标准误:5.20是自举样本平均数标准误的平均 计 自样本变侧 平均散形标准诞或 数.其最大差异达到(5.85-4.77)/1.53 0.706个标准误.而具有相应定义的3个样本 16.02.6 = 2381 标准差的标准误(,)4.14,483和3.68,其最大 差异达到(483 .68)/1.08 1.05个标 .0 21.43 5.16 误.它们虽然都未达到显着水平,但与:和 相比,差异有扩大趋势.这表明标准差有较大的抽样变异, 3)不论观察样本或自举样本,平均数夕都大于中位数M.这表明表1的潜伏期资料是左偏分 布.所以用21.47士5.16描述潜伏期(即有50%的沙门氏菌食物中毒患者是在取食后21.47h内发 病的,具标准误5.16h)可能比算术平均数更恰当。 3多变量自举 3.1方法 多变量自举又称成组自举,它仅是单变量自举的简单推广.设观察资料为!个变数和每变数n个 变量,每一变量可记为X(G=1,2,…,山j=1,2,…,).则在自举抽样时,1个随机数或变量号是代 表j=c(c为1,2,…,n中的某一指定值)时的一个变量组X,含1个变量:而每一自举样本则是由” 组各含【个变数的1个变量组成。其余方法和步骤都和单变量自举相同. 示例 表3的列2和3是水 场橘5号”12个植株的基部第1拔长节间粗度(X1,长径×短径,mm)和 其德部总粒数(X)的观结果四求得X和X的相关系数r和X,依 1的回归系数b为 a=r=∑xx/√云∑=0.8144, (5) A,=b=∑x1/∑-5.1217粒·mm3, 万方数
第l期 莫惠栋:重抽样技术——自举法 3 表l lo例沙门氏菌食物中毒息者的潜伏期(反/h)和3个自举样本 Table 1 Incubatj帆period(融/h)of lo sufferen from s口f珊肌棚口8Ⅱd 3 bootst哺p轴mpl雌 偏估计数. 2)3个样本平均数的标准误(s,)来自各不 相同的定义:5.8s是基于观察样本随机抽自正 态总体的假设;4.77是自举样本平均数分布的 标准误;5.20是自举样本平均数标准误的平均 数.其最大差异达到(5.85—4.77)/1.53= o.706个标准误.而具有相应定义的3个样本 标准差的标准误(s)4.“,4.83和3.68,其最大 差异达到(4.83—3.68)/1.08=1.065个标准 误.它们虽然都未达到显著水平,但与口:和魏 表2表l资料自举抽样各统计数的 平均数和标准误(m—l∞) Ttble 2 Avtra窖e nhd staⅡ血rd error or 100 boonnp疆mpIes f时Th蝴e l d●“ h 相比,差异有扩大趋势.这表明标准差有较大的抽样变异. 3)不论观察样本或白举样本,平均数,都大于中位数埘z这表明表l的潜伏期资料是左偏分 布.所以用21.47±5.16描述潜伏期(即有50%的沙门氏菌食物中毒患者是在取食后21.47 h内发 病的,具标准误5.16 h)可能比算术平均数更恰当. 3多变量自举 3.1方法 多变量自举又称成组自举,它仅是单变量自举的简单推广.设观察资料为f个变效和每变数n个 变量,每一变量可记为五』(净1,2,…,z;j一1,2,…,n).则在自举抽样时,1个随机数或变量号是代 表J=co为l,2,…,”中的某一指定值)时的一个变量组置。,含f个变量;而每一自举样本则是由n 组各含f个变效的1个变量组成.其余方法和步骤都和单变量自举相同. 3.2示例 表3的列2和3是水稻“扬襦5号”12个植株的基部第1拨长节间粗度(x,,长径×短径,mm2)和 其穗部总粒数(丘)的观察结果‘”.求得x,和xz的相关系数r和五依x,的回归系数6为: 吼=r一∑郴:/√∑z{·∑zz_o.81“,I … 晚一6一∑z。屯/∑z滓5.121 7粒·mm~.J 万方数据

4 扬州大学学报(自然科学饭 第4举 表3水稻扬横5号”植株基部第1拔长节间粗度(X:/mm)和德部较数X,)及其两个自举样本 Tabl 观变量 组号 X X: 随机号 X: 随机号 组梦 .5979 0.087 15 p10 10 1 026 8901 26 2 164 0.1726 9.3 0.8452 14. 0.8144 0.846 07351 5.1217 46739 (5)中的1=(X1一五),=(X:一玉).由于此例m=12,故自举随机号的分组数列为:(0一0.083 0.166~0.2500.3330.416~0.500~0.583~0.666~0.750~0.833-0.916~1.000).其第1、 第2自举样本和根据(5)式算得的0:也一并列于表3. 这里可注意:通常的相关系数标准误是在总体相关系数P=0的假设下给出的.此处r= 0.8144,为极显着,所以常规方法不能得到其标准误。当完成m一100次自举抽样,我们就有了,的 抽样分布,因而其平均数将是时0的数值估计,其标准差即是该相关系数的标准误估计, 4离回归自举 41方法 上节的多变数自举方法也完全适用于回归问题,只要将个变数中的1个(或几个)变数以Y,表 示.这时每一随机号代表一个变量组X(=1,2,,【一1)+Y。但据研究,纯粹的回归间题,即观 察变量能够明确区分为自变数和依变数的问题,应用离回归自举研究其统计数性质,可能都会比一般 化的多变量自举更好 因为自变数是固定的,理论上不存在随机误差, 设有依变数Y和个自变数X,(=1,2,,D,则回归分析的工作模型为 y,=a+6xy+0=12,…) (6) 如果记,=a+6X则有: EY-Y (7) 离回归自举就是1个随机数代表1个离回归值每轮自举抽样都得到个“新”的,值(记为): 然后构成Y: YEY+e (8) 并以Y:为依变数,X为自变数进行自举样本的回妇分析.这是X不变面Y,改变为Y:的自举抽 样.其余同前.MINITAB是此种抽样分析的 一个专用软件倒 4.2示例 表4的列2和列3是欧洲10国钢铁业1974年(X)和1992年(Y)的座员数(千人)们.由之可得 万方数据
4 扬州大学学报(自然科学版) 第4卷 表3水稻“扬糯s号”植株基部第1拔长节间根度(x。/mm2)和穗部粒数(托)及其两个自举样本 Table 3 Thickn螂0f the lst eIongatioⅡinterIL0de(X/mm2)and p^山de spjkeIets(x2)of rjce cultjvar“Yangnuo 5”and 2 b∞tstr。p疆mPJ蜉 (5)中的z-;(xz一至t),zz;(置~而).由于此例n=12,故自举随机号的分组数列为:(o~0.083~ o.16÷~o.250~o.33§~o.41;~o.500~o.58j~o.666~o.750~o.83§~o.916~1.000).其第1、 第2自举样本和根据(5)式算得的a:也一并列于表3. 这里可注意:通常的相关系数标准误是在总体相关系数P—o的假设下给出的.此处r= o.814 4,为极显著,所以常规方法不能得到其标准误.当完成m一100次自举抽样,我们就有了r的 抽样分布,因而其平均数将是P≠o的数值估计,其标准差即是该相关系数的标准误估计. 4离回归自举 4.1方法 上节的多变数自举方法也完全适用于回归问题,只要将f个变数中的1个(或几个)变数以n表 示.这时每一随机号代表一个变量组墨(f;1,2,…,z一1)+E.但据研究,纯粹的回归问题,即观 察变量能够明确区分为自变效和依变数的问题,应用离回归自举研究其统计数性质,可能都会比一般 化的多变量自举更好一些.因为自变数是固定的,理论上不存在随机误差. 设有依变效y和f个自变数咒(i=1,2,…,f).则回归分析的工作模型为: f L=口+∑觑xⅡ+q(J一1,2,…,n). (6) f一1 f 如果记P,=n+∑魏x口,则有: ●-1 q=E一岛. (7) 离回归自举就是1个随机数代表1个离回归值唧.每轮自举抽样都得到”个“新”的。值(记为一); 然后构成yJ-: l了一L+i; (8) 并以F为依变数,如为自变数进行自举样本的回归分析。这是置,不变而玎改变为W的自举抽 样.其余同前.MINITAB是此种抽样分析的一个专用软件嗍. 4.2示例 , 表4的列2和列3是欧洲10国钢铁业1974年(x)和1992年(y)的雇员数(干人)….由之可得 万方数据
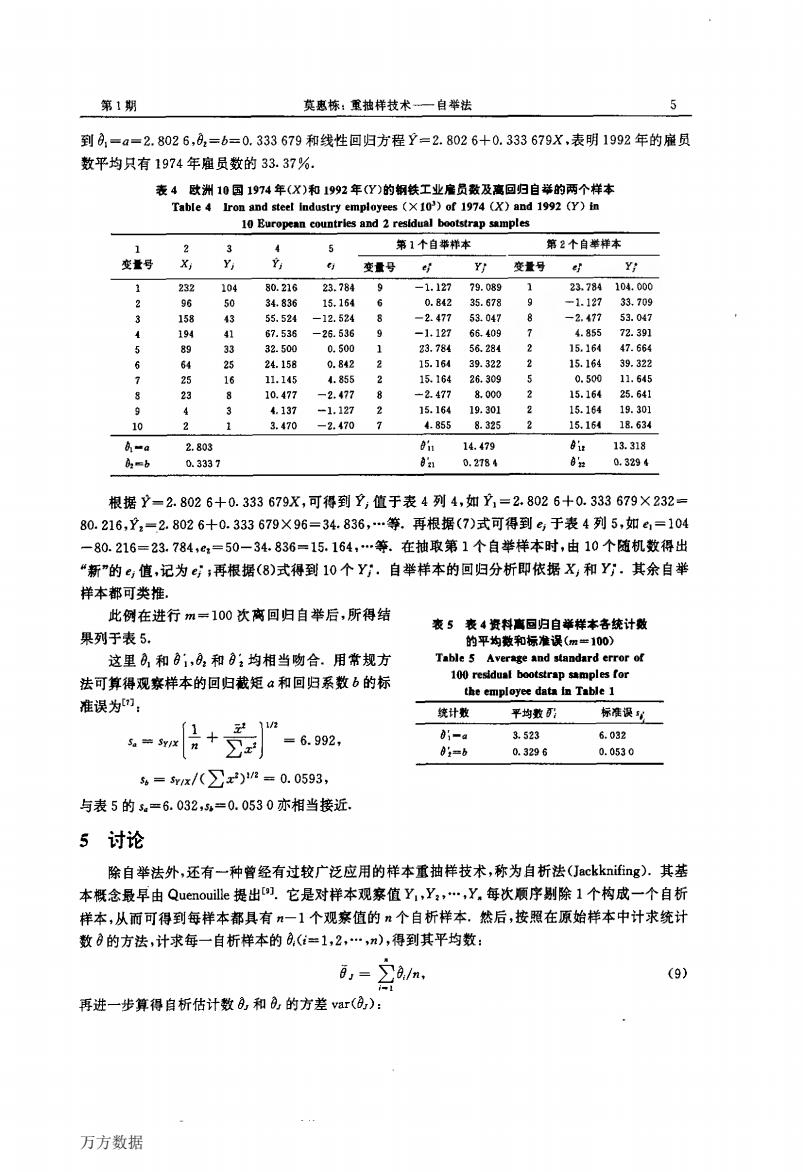
第1期 惠栋:重抽样技术一自举法 到月,=a=2.8026,8,=6=0.333679和线性回归方程Y=2.8026+0.333679X,表明1992年的m员 数平均只有1974年雇员数的33.37%. 表酒日n2车的楼想a酿的个牛 10 Ea ste 第1个自#样本 变量号 变量母 变量号 .70 234567890 87225222 65 15.16 19.30 55 根据Y-2.8026+0.333679X,可得到2,值于表4列4,如Y,=2.8026+0.333679×232= 80.216,-28026+0.333679×96=34.836,…尊.再根据(7)式可得到6于表4列5,如6,=104 一80.216=23.7844=50-34.836=15.164,…等.在抽取第1个自举样本时,由10个随机数得出 “新”的e,值,记为g:再根据(8)式得到10个Y;,自举样本的回归分析即依据X,和Y.其余自举 样本都可类推 此例在进行m一100次离回归自举后,所得结 果列于表5. 这里A和,A和:均相当吻合.用常规方 Table 5 Average and standard error of 法可算得观察样本的回归裁矩a和回归系数6的标 yes data in Table 1 准误为”: 计数 平均数 +是 =6.992, =srx/(∑2)n=0.0593, 与表5的=6.032=0.0530亦相当接近 5讨论 除自举法外,还有一种曾经有过较广泛应用的样本重抽样技术,称为自析法(Jockknifing).其菇 本概念最早由Quenouille提出.它是对样本观察值Y,Y,…,X,每次顺序别除1个构成一个自右 样本,从而可得到每样本都具有”一1个观察值的#个自析样本,然后,按照在原始样本中计求统计 数8的方法,计求每一自析样本的(=1,2,…,n),得到其平均数: 8.n (9) 再进一步算得自析估计数和的方差var(): 万方数据
第l期 奠惠栋:重抽样技术——自举法 5 到a。一d一2.802 6,吼=6=o.333 679和线性回归方程P=2.802 6+o.333 679x,表明1992年的雇员 数平均只有1974年雇员数的33.37%. 表4殴洲10国1974年(x)和19,2年(y)的钢铁工业雇员数殛离回归自举的两个样本 hbIe 4 Ir蛆蛐d netI induslq empIoy盹s(X 103)of 1974仪)and 1”2(y)王n 10 EuropHⅡcouⅡtrl曙a们2 r蛞岫u蝴b∞tsIr_p s枷pl酷 根据P=2.802 6+o.333 679x,可得到E值于表4列4,如矗=2.802 6+o.333 679×232; 80.216,P:一2.802 6+o.333 679×96=34.836,…等.再根据(7)式可得到岛于表4列5,如如=104 —80.216—23.784,缸一50一34.836=15.164,…等.在抽取第1个自举样本时。由10个随机数得出 “新”的q值,记为一;再根据(8)式得到10个y,.自举样本的回归分析即依据五和珂.其余自举 样本都可类推. 此例在进行”2100次离回归自举后,所得结 表5表4资料_回归自举样本备统计数 果列于表5· 的平均数和标准误(m=1们) 这里吼和aj,巩和a:均相当吻合.用常规方 T-Me 5^Ver_铲-Ⅱd shnd·rd ermr 0f 法可算得观察样本的回归截矩n和回归系数6的标 1≮0篙::慧=:=” 准误为。1:——磊i———i丽五F——1磊夏i一 矗~叫音+袁J刮瑚z, 怒 :赢 僦。 轧;卸,x/(∑一)…一o.0593, 与表5的L=6.032,“=0.053 0亦相当接近. 5讨论 除自举法外,还有一种曾经有过较广泛应用的样本重抽样技术,称为自析法(J”kknifing).其基 本概念最早由Quenounk提出‘”.它是对样本观察值y。,E,…,yl每次顺序剔除1个构成一个自析 样本,从而可得到每样本都具有n一1个观察值的n个自析样本.然后,按照在原始样本中计求统计 数a的方法,计求每一自析样本的鼠(净1,2,…,n),得到其平均数: 口,一∑鼠A, (9) 百 再进一步算得自析估计数以和良的方差var(以): 万方数据