
14 MECHANICAL FUNDAMENTALS makes an angle with the y axis.The normal stress is given by D a cos0 (1-7) The shear stress in the plane acts along the line OC and has the magnitude P T=-sin A (1-8) This shear stress may be further resolved into components parallel to the x and y directions lying the plane. P x direction T=sin sinφ (1-9) A P y direction TA sin8cosφ (1-10) Therefore,in general a given plane may have one normal stress and two shear stresses acting on it. 1-9 CONCEPT OF STRAIN AND THE TYPES OF STRAIN In Sec.1-4 the average linear strain was defined as the ratio of the change in length to the original length of the same dimension. 8 AL L-Lo e= LoLo Lo where e=average linear strain 8=deformation By analogy with the definition of stress at a point,the strain at a point is the ratio of the deformation to the gage length as the gage length approaches zero. Rather than referring the change in length to the original gage length,it often is more useful to define the strain as the change in linear dimension divided by the instantaneous value of the dimension. Lo (1-11) The above equation defines the natural,or true,strain.True strain,which is useful in dealing with problems in plasticity and metal forming,will be discussed more fully in Chap.3.For the present it should be noted that for the very small strains for which the equations of elasticity are valid the two definitions of strain give identical values. Not only will the elastic deformation of a body result in a change in length of a linear element in the body,but it may also result in a change in the initial angle

INTRODUCTION 15 Figure 1-7 Shear strain. between any two lines.The angular change in a right angle is known as shear strain.Figure 1-7 illustrates the strain produced by the pure shear of one face of a cube.The angle at A,which was originally 90,is decreased by the application of a shear stress by a small amount 6.The shear strain y is equal to the displace- ment a divided by the distance between the planes,h.The ratio a/h is also the tangent of the angle through which the element has been rotated.For the small angles usually involved,the tangent of the angle and the angle (in radians)are equal.Therefore,shear strains are often expressed as angles of rotation. a Y=方=tan8=0 (1-12) 1-10 UNITS OF STRESS AND OTHER QUANTITIES The International System of Units,usually called SI (for Systeme International), is followed in this book and is summarized in Appendix A.There are seven base SI units for measuring quantities,namely meter(m)for length,kilogram (kg)for mass,second (s)for time,ampere (A)for electric current,kelvin (K)for thermo- dynamic temperature,mole (mol)for amount of a substance,and candela(cd)for luminous intensity.All other units are derived from these. Some of the derived units have special names.For example,frequency is measured in units of s(i.e.per second),and this unit is known as the hertz (Hz);force is measured in units of m kg s-2(i.e.the force required to accelerate one kg to an acceleration of one meter per second squared),and this derived unit is called the newton (N);stress has dimensions of force per unit area and is therefore measured in units of N m2,which is known as the pascal (Pa).Note that since the acceleration due to gravity is 9.807 m s-2,a load of 1 kg exerts a force of 9.807 N.It can be seen from Appendix A that although different quan- tities may be expressed in different derived units,the units may be identical when expressed in base units(e.g.stress and energy density). In order to avoid describing quantities by very large or small numbers explic- itly,a system of prefixes is used to indicate multiples of a unit (see Appendix A). For example,a stress of 1 Pa is very small,and most stresses of practical interest are in the range 106 Pa to 1011 Pa.This range is more conveniently expressed using multiples as 1 MPa to 100 GPa.Units in a product are separated in this

16 MECHANICAL FUNDAMENTALS book by a space,e.g.MJ m-3 not MJm-3:this is not strictly necessary but is an aid to clarity. Finally it should be reemphasized that strain is simply a number.It is a dimensionless quantity and is not expressed in physical units. Example The shear stress required to nucleate a grain boundary crack in high-temperature deformation has been estimated to be 3πYbG 11/2 T= 8(1-v)L where y is the grain boundary surface energy,let us say 2 J m-2;G is the shear modulus,75 GPa;L is the grain boundary sliding distance,assumed equal to the grain diameter 0.01 mm,and v is Poisson's ratio,v=0.3.To cal- culate T we need to be sure the units are consistent and that the prefixes have been properly evaluated. To check the equation express all units in newtons and meters. 12 m 'N2\1/2N m =m2 Note that a joule (J)is a unit of energy;J =N m (see Appendix A) 3π×2×75×109 1/2 T= 8(1-0.3)×10-2×10-3 =(252.4×10141/2 =15.89×107Nm-2 =158.9MNm-2=158.9MPa BIBLIOGRAPHY Caddell,R.M.:"Deformation and Fracture of Solids,"Prentice-Hall Inc.,Englewood Cliffs,N.J., 1980. Felbeck,D.K.,and A.G.Atkins:"Strength and Fracture of Engineering Solids,"Prentice-Hall Inc., Englewood Cliffs,N.J.,1984. Gordon,J.E.:"Structures-or Why Things Don't Fall Through the Floor,"Penguin Books,London, 1978. Hertzberg,R.W.:"Deformation and Fracture Mechanics of Engineering Materials,"2d ed.,John Wiley Sons,New York,1983. LeMay,I.:"Principles of Mechanical Metallurgy,"Elsevier North-Holland Inc.,New York,1981. Meyers,M.A.,and K.K.Chawla:"Mechanical Metallurgy:Principles and Applications,"Prentice- Hall Inc.,Englewood Cliffs,N.J.,1984. Polakowski,N.H.,and E.J.Ripling:"Strength and Structure of Engineering Materials,"Prentice-Hall Inc.,Englewood Cliffs,N.J.,1964

CHAPTER TWO STRESS AND STRAIN RELATIONSHIPS FOR ELASTIC BEHAVIOR 2-1 INTRODUCTION The purpose of this chapter is to present the mathematical relationships for expressing the stress and strain at a point and the relationships between stress and strain in a solid which obeys Hooke's law.While part of the material covered in this chapter is a review of information generally covered in strength of materials, the subject is extended beyond this point to a consideration of stress and strain in three dimensions.The material included in this chapter is important for an understanding of most of the phenomenological aspects of mechanical metallurgy, and for this reason it should be given careful attention by those readers to whom it is unfamiliar.In the space available for this subject it has not been possible to carry it to the point where extensive problem solving is possible.The material covered here should,however,provide a background for intelligent reading of the more mathematical literature in mechanical metallurgy. It should be recognized that the equations describing the state of stress or strain in a body are applicable to any solid continuum,whether it be an elastic or plastic solid or a viscous fluid.Indeed,this body of knowledge is often called continuum mechanics.The equations relating stress and strain are called constitu- tive equations because they depend on the material behavior.In this chapter we shall only consider the constitutive equations for an elastic solid. 2-2 DESCRIPTION OF STRESS AT A POINT As described in Sec.1-8,it is often convenient to resolve the stresses at a point into normal and shear components.In the general case the shear components are at arbitrary angles to the coordinate axes,so that it is convenient to resolve each 17
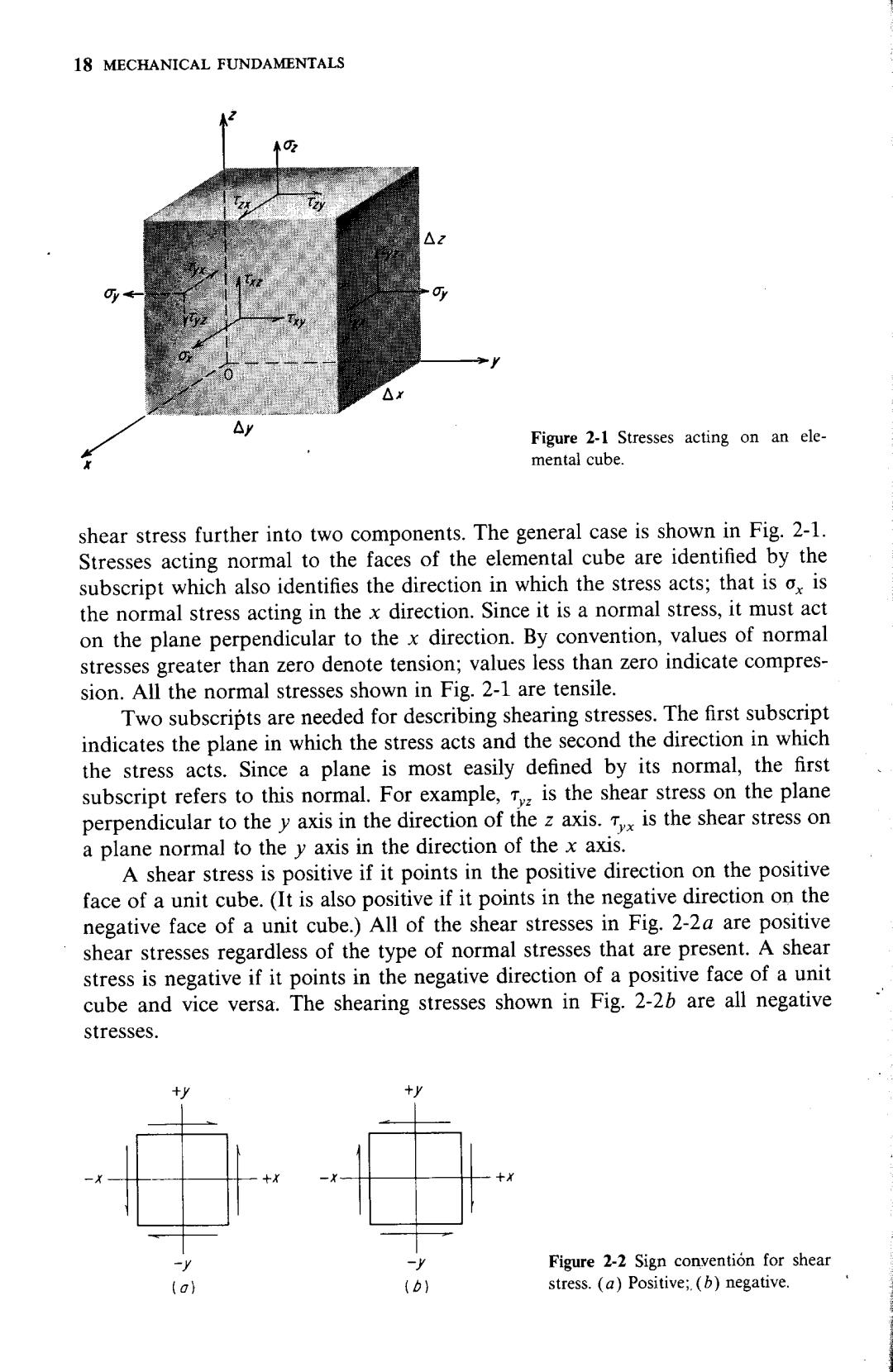
18 MECHANICAL FUNDAMENTALS △X △ Figure 2-1 Stresses acting on an ele- mental cube. shear stress further into two components.The general case is shown in Fig.2-1. Stresses acting normal to the faces of the elemental cube are identified by the subscript which also identifies the direction in which the stress acts;that is o,is the normal stress acting in the x direction.Since it is a normal stress,it must act on the plane perpendicular to the x direction.By convention,values of normal stresses greater than zero denote tension;values less than zero indicate compres- sion.All the normal stresses shown in Fig.2-1 are tensile. Two subscripts are needed for describing shearing stresses.The first subscript indicates the plane in which the stress acts and the second the direction in which the stress acts.Since a plane is most easily defined by its normal,the first subscript refers to this normal.For example,T is the shear stress on the plane perpendicular to the y axis in the direction of the z axis.is the shear stress on a plane normal to the y axis in the direction of the x axis. A shear stress is positive if it points in the positive direction on the positive face of a unit cube.(It is also positive if it points in the negative direction on the negative face of a unit cube.)All of the shear stresses in Fig.2-2a are positive shear stresses regardless of the type of normal stresses that are present.A shear stress is negative if it points in the negative direction of a positive face of a unit cube and vice versa.The shearing stresses shown in Fig.2-2b are all negative stresses. -V Figure 2-2 Sign convention for shear (a) (b) stress.(a)Positive;(b)negative