
STRESS AND STRAIN RELATIONSHIPS FOR ELASTIC BEHAVIOR 19 The notation for stress given above is the one used by Timoshenko and most American workers in the field of elasticity.However,many other notations have been used,some of which are given below Ox 011 Xx Xx Pxx Oy 022 Y, y Pyy 02 033·Z2 22 Piz Txy 012 xy pxy Tyz 023 Y, yz Pyz T:x 031 Zx 2x Pzx It can be seen from Fig.2-1 that nine quantities must be defined in order to establish the state of stress at a point.They are ox,,,Txz,Tyx,T,Tx andTHowever,some simplification is possible.If we assume that the areas of the faces of the unit cube are small enough so that the change in stress over the face is negligible,by taking the summation of the moments of the forces about the z axis it can be shown that Txy=Tyx. (Txy△y△z)△x=(Tx△x△z)△y (2-1) .∴.Txy=Tyx and in like manner Txz=T2x Tyz Tzy Thus,the state of stress at a point is completely described by six components: three normal stresses and three shear stresses,ox,oy,o,Txy,Txz,Tyz 2-3 STATE OF STRESS IN TWO DIMENSIONS (PLANE STRESS) Many problems can be simplified by considering a two-dimensional state of stress.This condition is frequently approached in practice when one of the dimensions of the body is small relative to the others.For example,in a thin plate loaded in the plane of the plate there will be no stress acting perpendicular to the surface of the plate.The stress system will consist of two normal stresses o,and o,and a shear stressxA stress condition in which the stresses are zero in one of the primary directions is called plane stress. Figure 2-3 illustrates a thin plate with its thickness normal to the plane of the paper.In order to know the state of stress at point O in the plate,we need to be able to describe the stress components at o for any orientation of the axes through the point.To do this,consider an oblique plane normal to the plane of the paper at an angle between the x axis and the outward normal to the oblique plane.Let the normal to this plane be the x'direction and the direction lying in 1 S.P.Timoshenko,and J.N.Goodier,"Theory of Elasticity,"2d ed.,McGraw-Hill Book Company,New York,1951

20 MECHANICAL FUNDAMENTALS Figure 2-3 Stress on oblique plane (two dimensions). the oblique plane the y'direction.It is assumed that the plane shown in Fig.2-3 is an infinitesimal distance from O and that the element is so small that variations in stress over the sides of the element can be neglected.The stresses acting on the oblique plane are the normal stress o and the shear stress T.The direction cosines between x'and the x and y axes are and m,respectively.From the geometry of Fig.2-3,I=cos and m sin 0.If A is the area of the oblique plane,the areas of the sides of the element perpendicular to the x and y axes are Al and Am. Let S and S,denote the x and y components of the total stress acting on the inclined face.By taking the summation of the forces in the x direction and the y direction,we obtain SxA =0xAl Txy Am S,A =Oy Am TxyAl or Sx=ox cos 6+Txy sin Sy =oy sin Txy cos The components of S and S,in the direction of the normal stress o are SN=S.cos 0 and SN=S,sin0 so that the normal stress acting on the oblique plane is given by Ox=Sx cos S sin (2-2) ox=ox cos20+o sin20 2Txy sin 0 cos 0 The shearing stress on the oblique plane is given by Tx'y=S,cos-Sx sin b (2-3) Tx=Tx (cos20-sin20)+(o-03)sine cos The stress o may be found by substituting +2 for in Eq.(2-2),since o is orthogonal to ox. c,=0xcos2(9+π/2)+0,sin2(8+π/2)+2 Txy sin(0+m/2)cos(0+π/2) and since sin(+7/2)=cos and cos(0 +/2)=-sin6,we obtain Oy=0x sin20+o cos20-2Txy sin 0 cos (2-4)

STRESS AND STRAIN RELATIONSHIPS FOR ELASTIC BEHAVIOR 21 Equations (2-2)to (2-4)are the transformation of stress equations which give the stresses in an x'y'coordinate system if the stresses in an xy coordinate system and the angle 6 are known. To aid in computation,it is often convenient to express Eqs.(2-2)to (2-4)in terms of the double angle 20.This can be done with the following identities: cos20+1 c0s20= 2 sin2 01-cos20 2 2sin0cos0=sin2θ cos20-sin20=cos 20 The transformation of stress equations now become ,+g+:g 0x= 2 2 cos 20+Tx sin 20 (2-5 s+ood c0s 20-sin 20 0p=- 2 (2-6) 2 'y= 2 sin 20+cos20 0y-0x (2-7) It is important to note that o+=ox+o.Thus the sum of the normal stresses on two perpendicular planes is an incariant quantity,that is,it is independent of orientation or angle 6. Equations(2-2)and (2-3)and their equivalents,Eqs.(2-5)and(2-7),describe the normal stress and shear stress on any plane through a point in a body subjected to a plane-stress situation.Figure 2-4 shows the variation of normal stress and shear stress with 6 for the biaxial-plane-stress situation given at the top of the figure.Note the following important facts about this figure: 1.The maximum and minimum values of normal stress on the oblique plane through point O occur when the shear stress is zero. 2.The maximum and minimum values of both normal stress and shear stress occur at angles which are 90 apart. 3.The maximum shear stress occurs at an angle halfway between the maximum and minimum normal stresses. 4.The variation of normal stress and shear stress occurs in the form of a sine wave,with a period of =180.These relationships are valid for any state of stress. For any state of stress it is always possible to define a new coordinate system which has axes perpendicular to the planes on which the maximum normal stresses act and on which no shearing stresses act.These planes are called the principal planes,and the stresses normal to these planes are the principal stresses. For two-dimensional plane stress there will be two principal stresses ot and o2 which occur at angles that are 90 apart(Fig.2-4).For the general case of stress
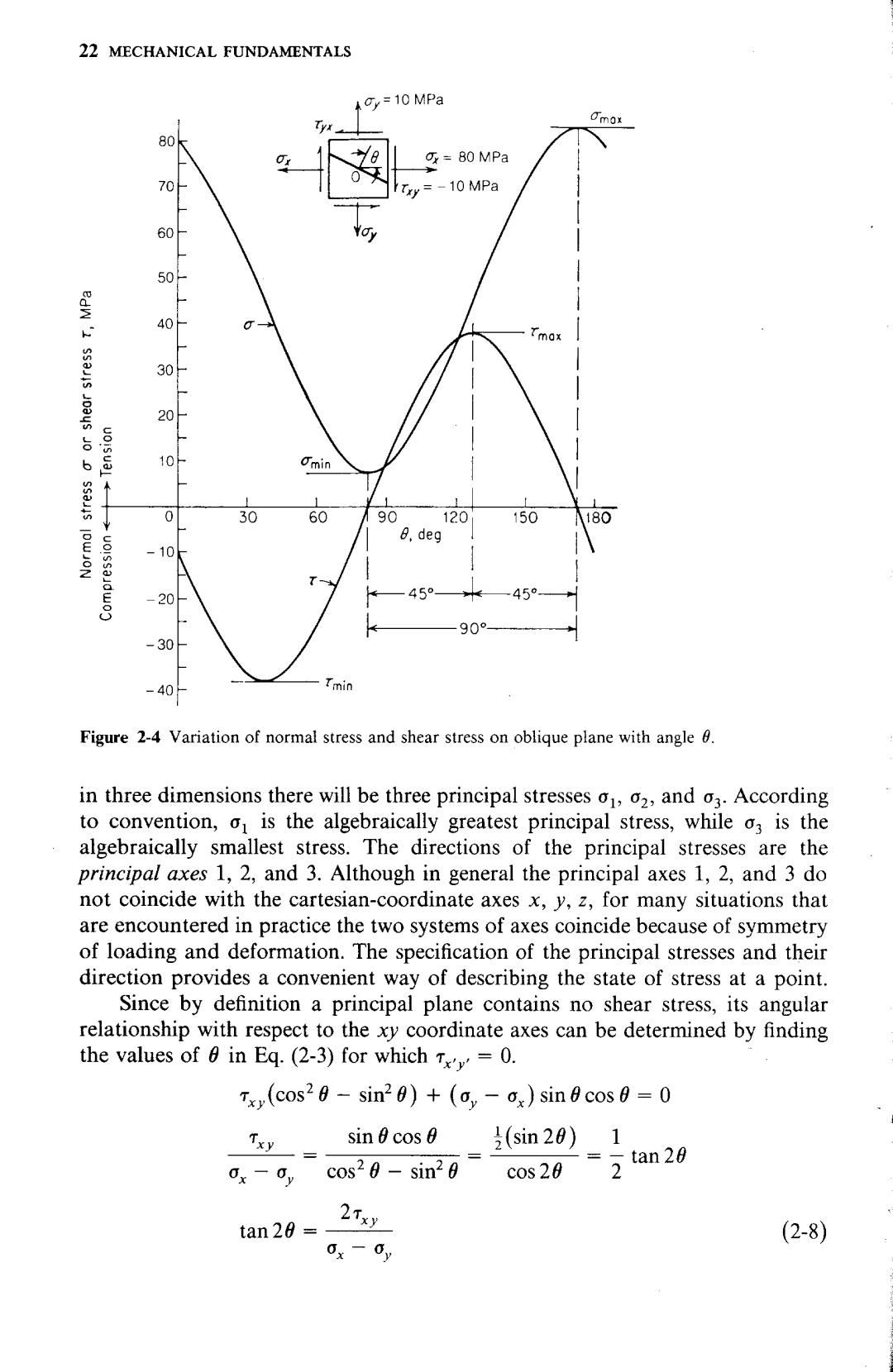
22 MECHANICAL FUNDAMENTALS y=10 MPa 80 80 MPa 70 =-10 MPa 60 50- 40 30 - 20 : 20152l 10 Omin 0 30 60 90 120 150 80 6,deg 10 20 45 45° 90° 30 40 Figure 2-4 Variation of normal stress and shear stress on oblique plane with angle 0. in three dimensions there will be three principal stresses o,02,and o3.According to convention,o is the algebraically greatest principal stress,while os is the algebraically smallest stress.The directions of the principal stresses are the principal axes 1,2,and 3.Although in general the principal axes 1,2,and 3 do not coincide with the cartesian-coordinate axes x,y,z,for many situations that are encountered in practice the two systems of axes coincide because of symmetry of loading and deformation.The specification of the principal stresses and their direction provides a convenient way of describing the state of stress at a point. Since by definition a principal plane contains no shear stress,its angular relationship with respect to the xy coordinate axes can be determined by finding the values of 6 in Eq.(2-3)for which T=0. Tx (cos20-sin20)+(a-ox)sine cos=0 sin0cos0(sin20)1 ox-oy cos20-sin20 cos 20 =2tan29 tan 20 = (2-8) 0x-0y

STRESS AND STRAIN RELATIONSHIPS FOR ELASTIC BEHAVIOR 23 Since tan 20 tan(m+20),Eq.(2-8)has two roots,0 and 02=0+n/2. These roots define two mutually perpendicular planes which are free from shear. Equation (2-5)will give the principal stresses when values of cos20 and sin 20 are substituted into it from Eq.(2-8).The values of cos 20 and sin 20 are found from Eq.(2-8)by means of the pythagorean relationships. 可xy m20=±o.-74+7 (ox-0)/2 cos20=± [《(.-o,/4+] Substituting these values into Eq.(2-5)results in the expression for the maximum and minimum principal stresses for a two-dimensional (biaxial)state of stress. 告±+ (2-9) The direction of the principal planes is found by solving for 6 in Eq.(2-8), taking special care to establish whether 20 is between 0 and 7/2,m,and 37/2, etc.Figure 2-5 shows a simple way to establish the direction of the largest principal stress o:o will lie between the algebraically largest normal stress and the shear diagonal.To see this intuitively,consider that if there were no shear stresses,then o=o.If only shear stresses act,then a normal stress(the principal stress)would exist along the shear diagonal.If both normal and shear stresses act on the element,then o lies between the influences of these two effects. To find the maximum shear stress we return to Eq.(2-7).We differentiate the expression for and set this equal to zero. 5y-(g,-a,Jcos20-2,sin20=0 do (2-10) tan20,= =9-0=-:-0 2Txy 2Txy Comparing this with the angle at which the principal planes occur,Eq.(2-8), tan 20=2(),we see that tan20,is the negative reciprocal of tan20 y>o Shear diagonal Figure 2-5 Method of establishing direction of o1