
§6.④狭义相对论时空观(View of Space and Time of Special Relativity) 经典 相对论 时间独立于空间 “同时”的相对性 时间测量与坐标系无关 时间膨胀 长度测量与坐标系无关 长度收缩
§6.4 狭义相对论时空观(View of Space and Time of Special Relativity) 经 典 相对论 时间独立于空间 “同时”的相对性 时间测量与坐标系无关 时间膨胀 长度测量与坐标系无关 长度收缩
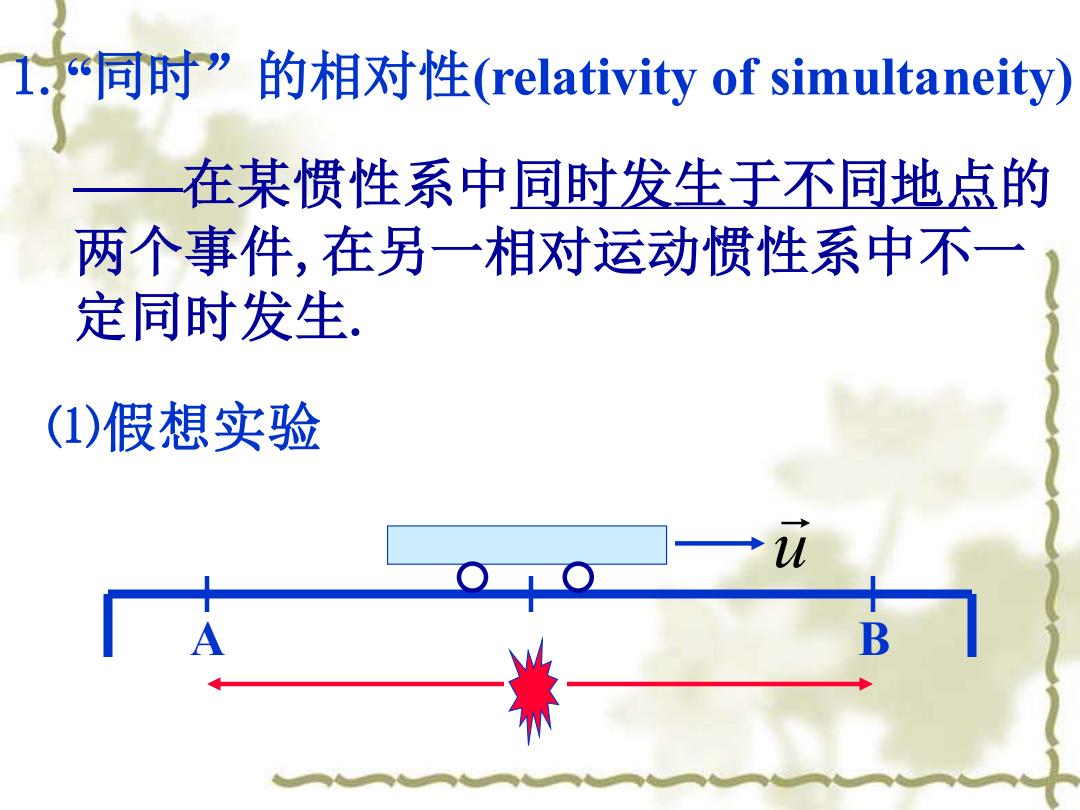
I.同时”的相对性(relativity of simultaneity) 在某惯性系中同时发生于不同地点的 两个事件,在另一相对运动惯性系中不一 定同时发生 (1)假想实验 B
1.“同时”的相对性(relativity of simultaneity) ——在某惯性系中同时发生于不同地点的 两个事件,在另一相对运动惯性系中不一 定同时发生. A B u ⑴假想实验
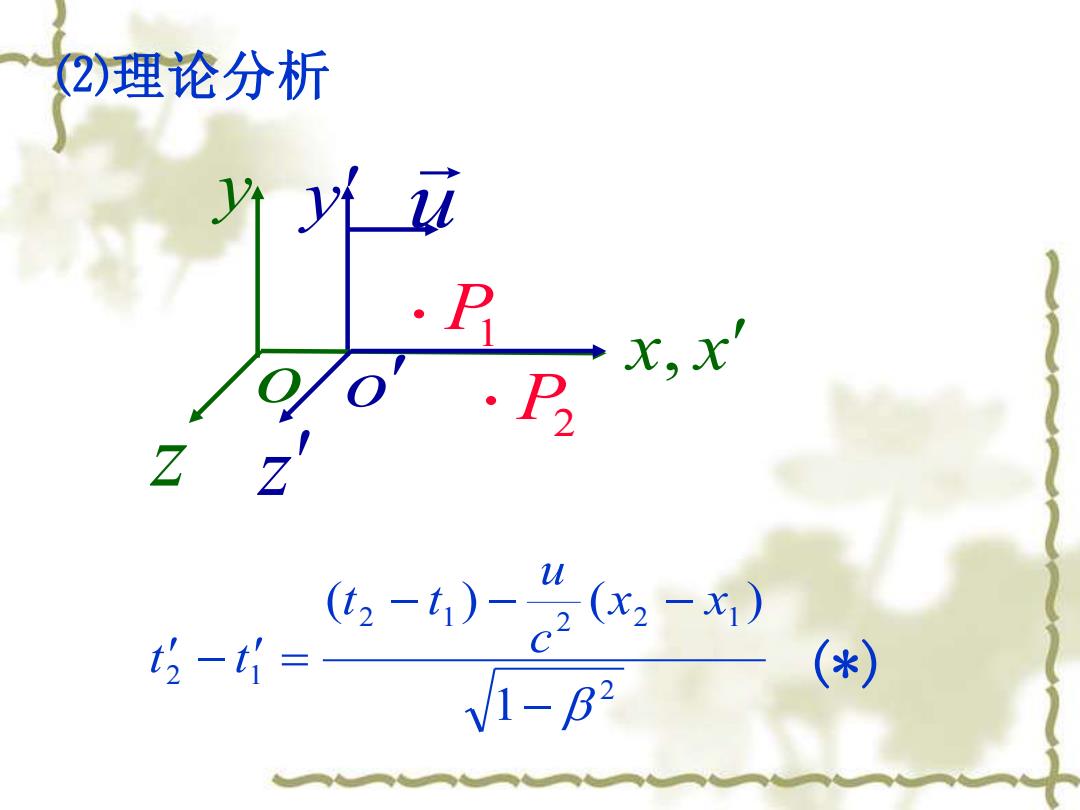
(2)理论分析 P .P2 ,x 6,-)-1-x) 5-t= (*) V1-B2
P1 x, x o y y u o z z P2 ⑵理论分析 2 2 1 2 2 1 2 1 1 ( ) ( ) − − − − − = x x c u t t t t (*)

若t2=t1,x2丰x 则巧≠ 若t2=t1,x2=x 则t巧=好 [思考]两事件“同时同地”、“同地不同 时”、“不同地不同时”,结果?
若 2 1 2 1 t = t , x x 则 2 1 t t 则 2 1 t = t 若 2 1 2 1 t = t , x = x [思考] 两事件“同时同地”、“同地不同 时”、“不同地不同时”,结果?

Note: 在不同惯性系中观测,两事件的时序 可能颠倒,但因果事件不会如此. 理由](*)式 、 (X2-X1) c2 t-t=(t2-t) (t2-t) V1-β2 因果事件间的信号传递速率: x2-x1 t2-t1 →(3-)与(2-)同号
在不同惯性系中观测,两事件的时序 可能颠倒,但因果事件不会如此. [理由] (*)式→ 2 2 1 2 1 2 2 1 2 1 1 ( ) ( ) 1 ( ) − − − − − = − t t x x c u t t t t 因果事件间的信号传递速率: c t t x x − − 2 1 2 1 →(t 2 −t 1 )与 (t 2 −t 1 )同号 Note: