安徽科技学院：《大学物理》课程教学资源（PPT课件）力学——第五章 刚体力学（刚体的定轴转动 Rotation of a Rigid Body About a Fixed Axis）

第四章 刚体的定轴转动 (Rotation of a Rigid Body About a Fixed Axis) 刚体：任意两质元间距离保持不变.（理想模型） 刚体的运动： ①平动- 各质元运动状态保持相同 ②转动一各质元绕同一轴作圆周运动 ③复合运动—平动十转动

第四章 刚体的定轴转动 (Rotation of a Rigid Body About a Fixed Axis) 刚体:任意两质元间距离保持不变.(理想模型) 刚体的运动: ③复合运动——平动＋转动 ①平动——各质元运动状态保持相同 ②转动——各质元绕同一轴作圆周运动

本章：（定轴转动运动学 定轴转动定律 转动中的功和能 定轴转动的角动量守恒定律

本章： 定轴转动运动学 定轴转动定律 转动中的功和能 定轴转动的角动量守恒定律

S4.1定轴转动运动学(Kinematics of Rotation About a Fixed Axis) 同“圆周运动” S = RO V= Ro a, Ra an = Ro 2

§4.1 定轴转动运动学 (Kinematics of Rotation About a Fixed Axis) ——同“圆周运动”  v  s R o t a  n a  S = R v = R at = R 2 an = R

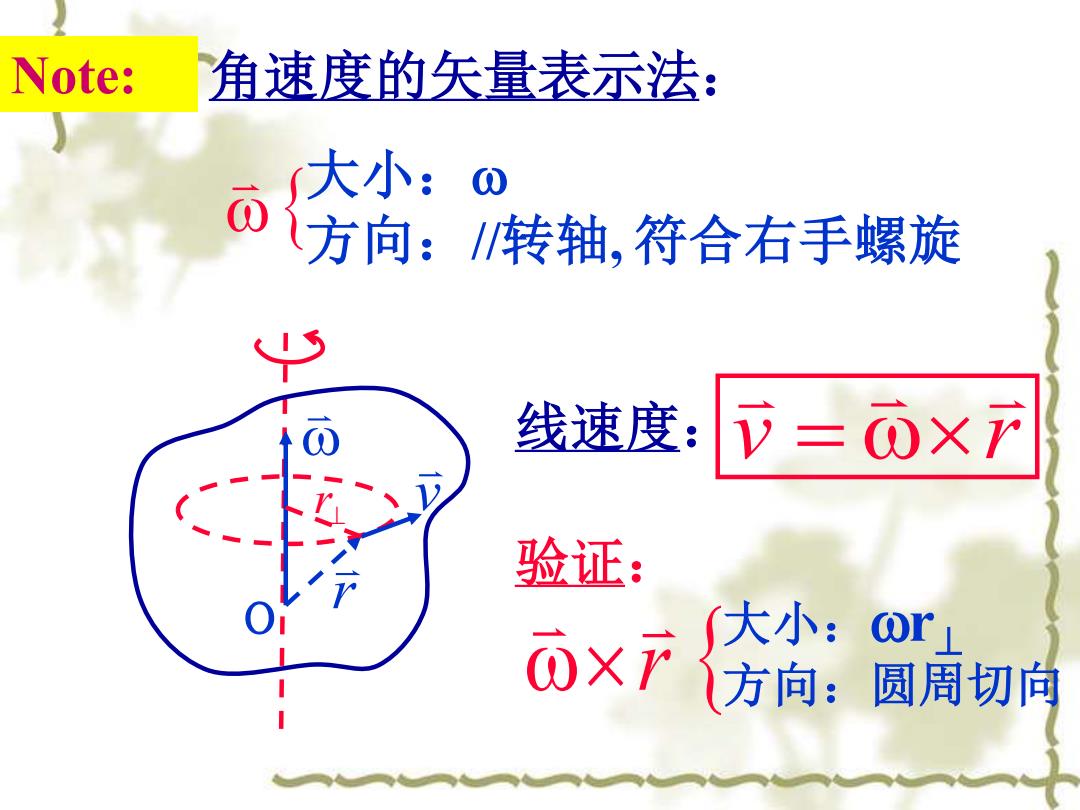
Note: 角速度的矢量表示法： 大小：0 方向：/转轴，符合右手螺旋 线速度： 验证： O×F 大小：Or 方向：圆周切向

角速度的矢量表示法：   大小： 方向：//转轴, 符合右手螺旋 Ｏ   r  ⊥ r v  线速度： v r    =  验证： r     大小：r⊥ 方向：圆周切向 Note:

例4-1已知：o=60 k rev/min F=(3i+4i+5k)×102m 求：立=？ 解：o=(60×2π/60)k=2成(rad/) 立=ōXF =2πk×(3i+4j+5k)×103 =(60-8m)×102 0.251i+0.188j(m/s)

例4-1 已知： 60k rev / min   = r i j k m 2 (3 4 5 ) 10− = + +      求： v = ?  解： k    = (602 / 60) 2 k (rad /s)  =  v r    =  2 2 (3 4 5 ) 10− = k  i + j + k       2 (6 8 ) 10− = j − i      0.251i 0.188 j (m/s)   = − +