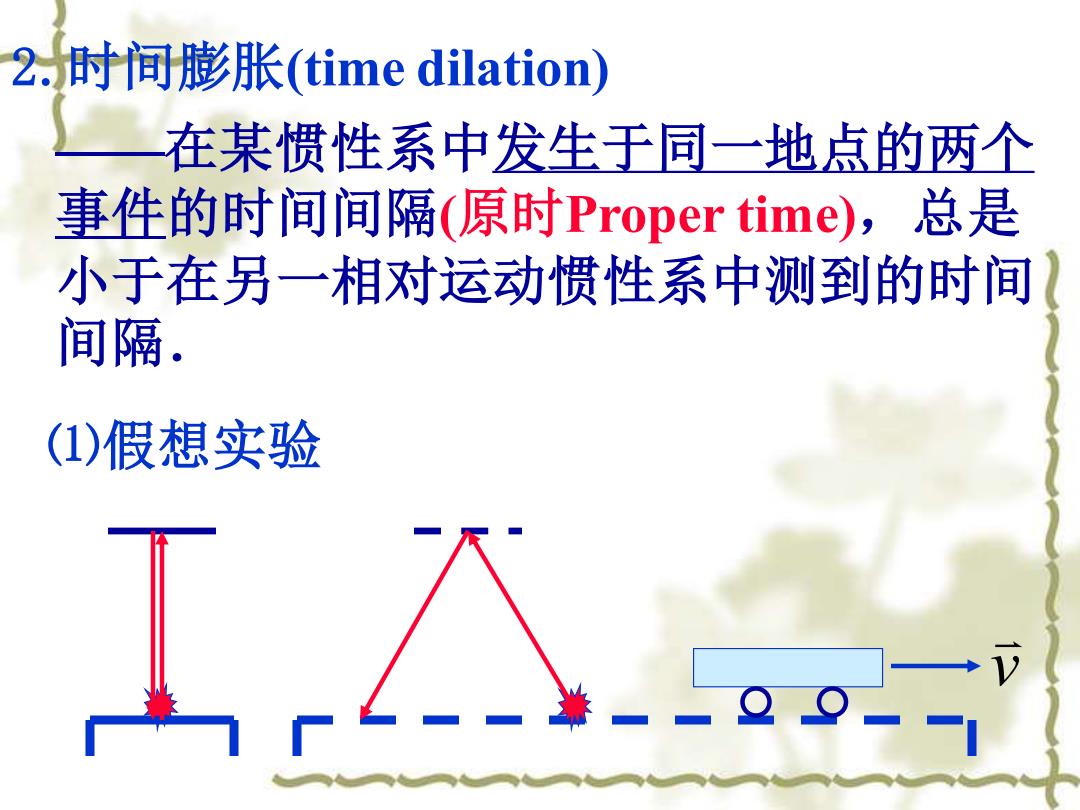
2.时间膨胀(time dilation) 在某惯性系中发生于同一地点的两个 事件的时间间隔(原时Proper time),总是 小于在另一相对运动惯性系中测到的时间 间隔. (1)假想实验
2.时间膨胀(time dilation) ——在某惯性系中发生于同一地点的两个 事件的时间间隔(原时Proper time),总是 小于在另一相对运动惯性系中测到的时间 间隔. v ⑴假想实验

(2)理论分析 6-)-4x-x) t行-t= V1-B2 令X2= →6-式=-B t2->t2-1
2 2 1 2 2 1 2 1 1 ( ) ( ) − − − − − = x x c u t t t t 令 2 1 x = x 2 1 2 2 1 2 1 1 t t t t t t − − − → − = ⑵理论分析
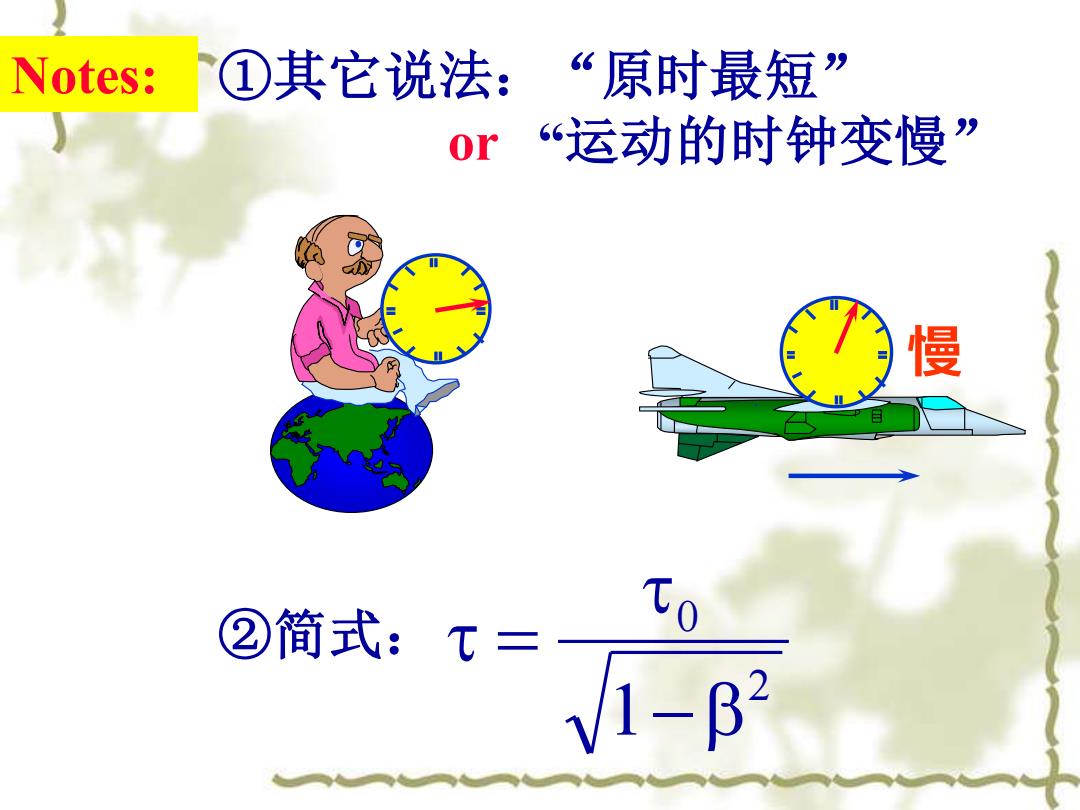
Notes: ①其它说法:“原时最短” or “运动的时钟变慢” 慢 ②简式:τ= To 1-B2
①其它说法:“原时最短” or “运动的时钟变慢” Notes: a. . 慢 ②简式: 2 0 1− =
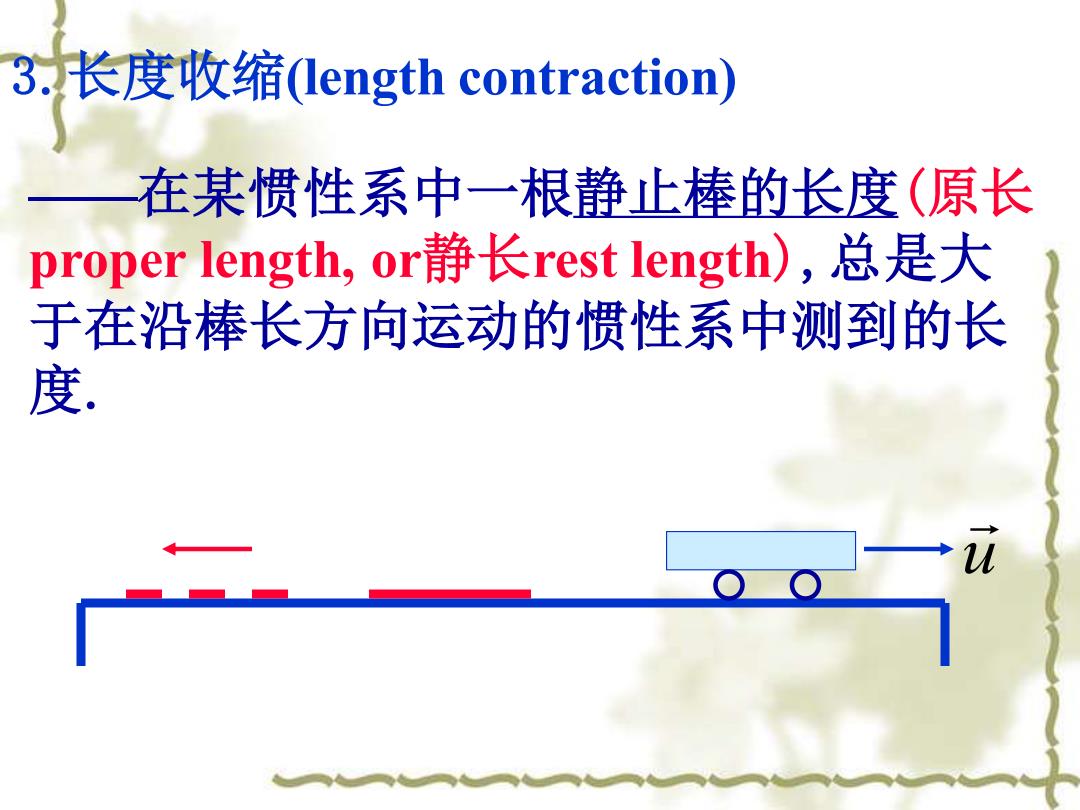
3.长度收缩(ength contraction) 在某惯性系中一根静止棒的长度(原长 proper length,or静长rest length),总是大 于在沿棒长方向运动的惯性系中测到的长 度
3.长度收缩(length contraction) ——在某惯性系中一根静止棒的长度(原长 proper length, or静长rest length),总是大 于在沿棒长方向运动的惯性系中测到的长 度. u
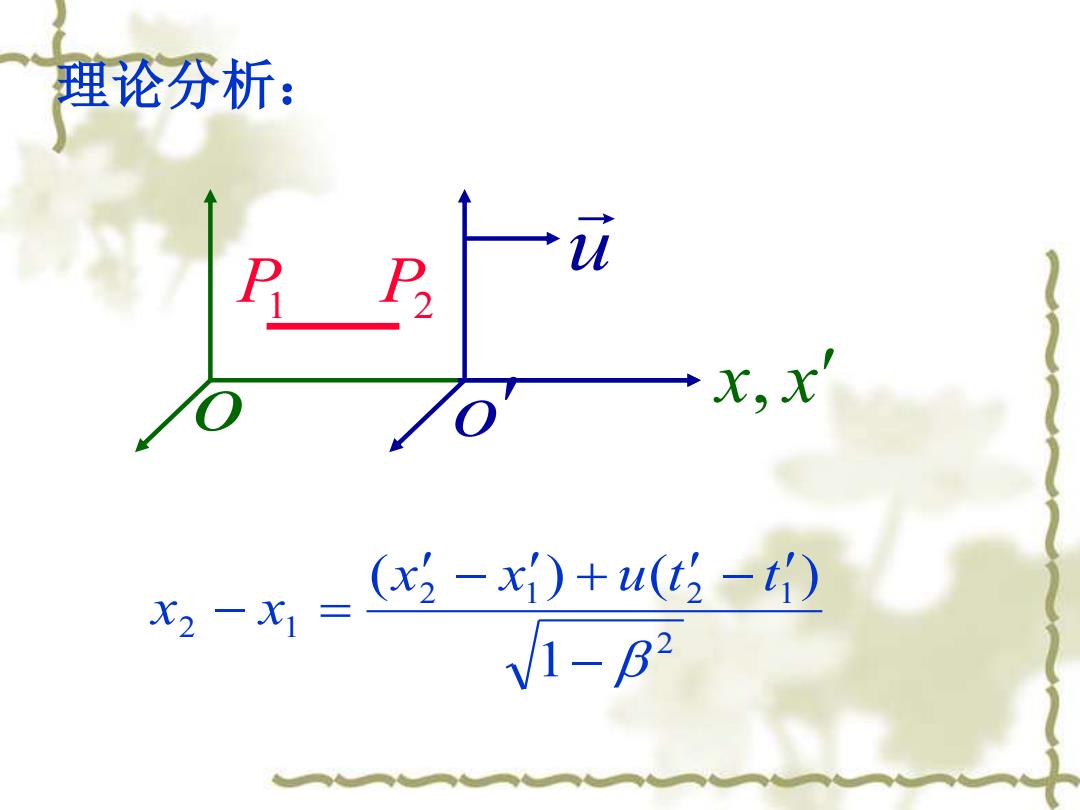
理论分析: x.x -x=任-x)+u-0 V1-B2
2 2 1 2 1 2 1 1 ( ) ( ) − − + − − = x x u t t x x 理论分析: P1 x, x u o P2 o