IV)理气的混合熵 1)等T,V混合 n P.TV+P."TV T'→,E,Ty n=nA+ng P=PA+PB 等T:△U=0,△U=0,△U=0 △H=0,△HB=0,△U=0 始态 终态 A T,V,PA T,V,PA △S= B T,V,PB T,V,PB
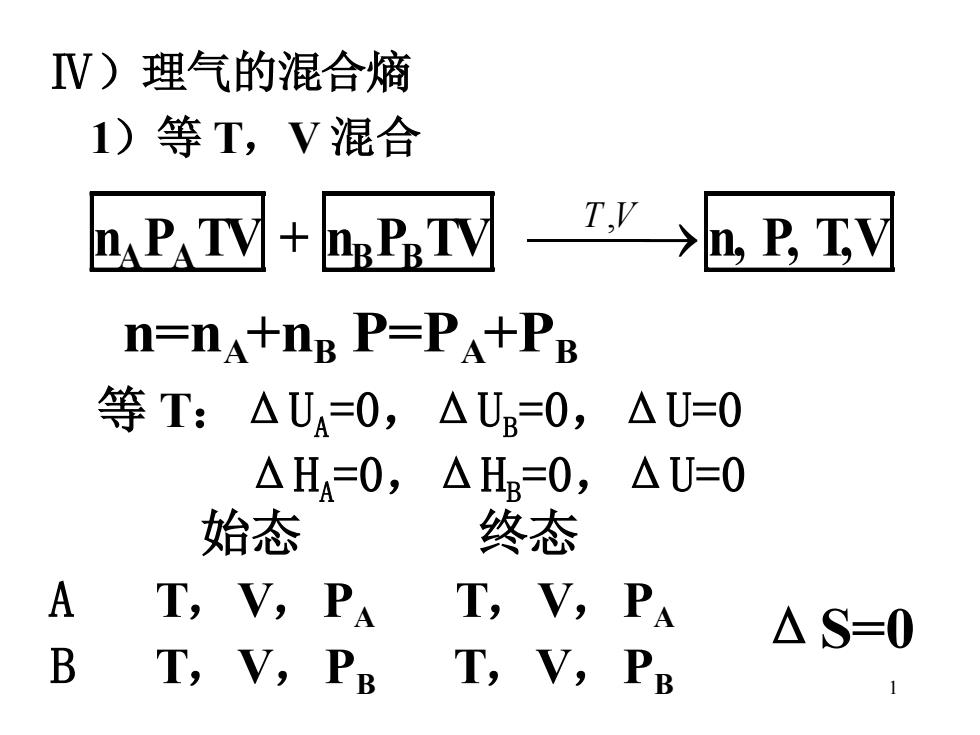
1 Ⅳ)理气的混合熵 1)等 T,V 混合 nA PA TV + nB PB TV ⎯T ⎯,V →n, P, T,V n=nA +nB P=PA +PB 等 T:ΔUA = 0,ΔUB = 0,ΔU=0 ΔHA = 0,ΔHB = 0,ΔU=0 始态 终态 A T,V,PA T,V,PA B T,V,PB T,V,PB ΔS=0

说明:a)始终态未变△S=0 b)两种不同理气等TV混合△S=0 c)相同理气混合相当于压缩,△S≠0 2)等T(P) 的混合 na VeTP+ne VeTP TP→n,V,T,E n=nA+nB,P=PA+PB,V=VA+VB 始态 终态 A VA,T,P T,V,PA V-V+VB B VB,T,P T,V,PB P=PA+Pp
2 说明:a)始终态未变ΔS=0 b)两种不同理气等 TV 混合ΔS=0 c)相同理气混合相当于压缩,ΔS≠0 2)等 T(P)的混合 n=nA +nB , P=PA +PB , V=VA + VB 始态 终态 A VA,T,P T,V,PA V=VA +VB B VB,T,P T,V,PB P=PA +PB nA VB TP + nB VB TP ⎯T ⎯,P →n , V , T , P
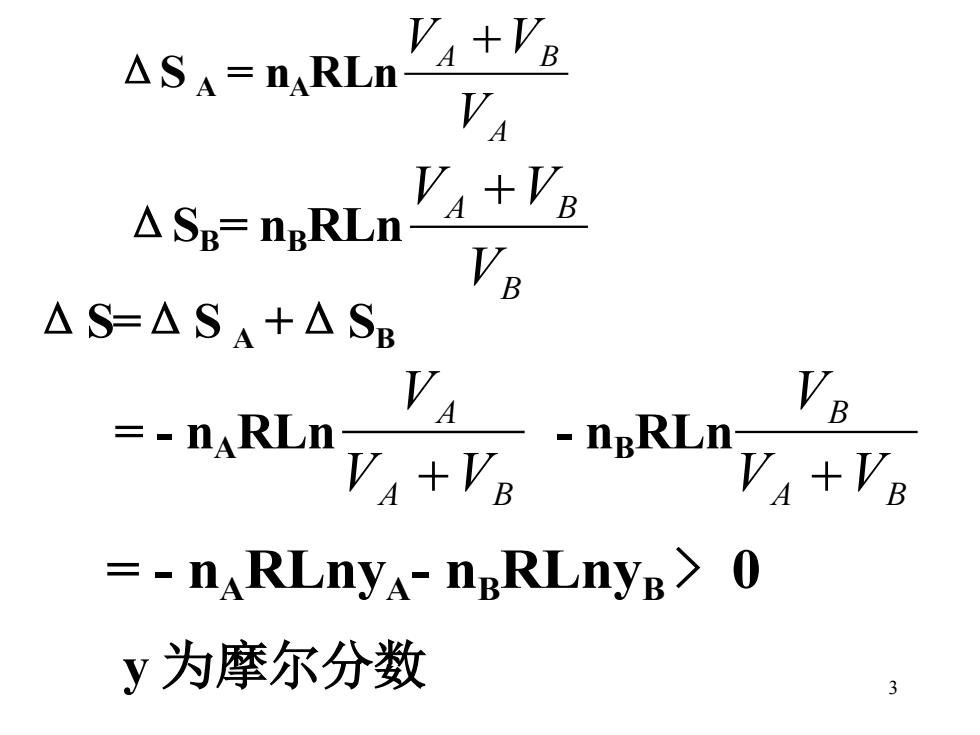
VA+VR △SA=naRn △SB=ngRLn △S=△SA+ASB -aRa,ap, VA =-nARLnyA-nBRLnyB>0 y为摩尔分数 3
3 ΔS A = nA RLn A A B V V +V ΔSB = nB RLn B A B V V +V ΔS=ΔS A +ΔSB = - nA RLn A B A V V V + - nB RLn A B B V V V + = - nA RLnyA- nB RLnyB > 0 y 为摩尔分数

△S环=-Q体/T=0 Q体=0 △S总=△S体=-nARLnyA-DERLnYB>0 绅业凹鐳最Lb婚号 AS-R∑n,Lny,>0 说明:a)等T,P混合,△S↑,V↑,活动空 间↑,混乱度增大 b)若为同种理气等T,P 状态没有发生变化混合△S=0
4 ΔS 环=-Q 体/T= 0 ΔS 总=ΔS 体= - nARLnyA- nBRLnyB >0 几种不同理气等 T,P混合: ΔS= -R i n i ni Lny > 0 说明:a)等 T,P 混合,ΔS↑ ,Vi↑,活动空 间↑,混乱度增大 b)若为同种理气等 T, P Q 体=0 状态没有发生变化 混合ΔS=0

△S 等T,V 等T,P 不同理气 △S=0 AS-R∑n,Ly 相同理气 △S≠0 △S=0 2.相变化过程的熵变 相变化:在一定条件下,物质从一种聚集态 变到另一种聚集态 聚集态:汽,液,固,g,1,s表示 1)可逆相变化:
5 2. 相变化过程的熵变 相变化:在一定条件下,物质从一种聚集态 变到另一种聚集态 聚集态:汽,液,固,g,l,s 表示 1)可逆相变化: c) ΔS 等 T,V 等 T,P 不同理气 ΔS= 0 ΔS= -R i n i ni Lny 相同理气 ΔS≠0 ΔS= 0