
第二章频率综合器的结构 H(s)是低通滤波器的传输函数:Ky是VCO的压控增益:N是分频器的分频比。 2.2.2开环分析法 由于频率综合器是反馈系统,反馈系统可以用开环传输函数和反馈系数来表示闭 环传输函数。对于频率综合器的线性模型,其开环传输函数Hs为: H(s)= KpKy H(s) (2-1) N 其反馈系数是1N,则闭环传输函数Hcs为: NH (s) H.(S)=1+HS (2-2) 通常由于开环传输函数比较简单,而且易于分析,所以通常用开环特性分析替代闭 环特性分析。对于典型的二阶环路滤波器,即 H(s)=_5+@. (2-3) s(s+0。) 其开环传输函数Hs的Bode图如图2.3所示,其中开环增益为0dB的频率点ωc 称为环路带宽:在0。处的开环相位也被称为相位裕度。通过对开环传输函数的环路 带宽和相位裕度的设计可以方便的得到环路参数。值得注意的是,这里的模型是连 续时间模型,而实际的环路具有离散的特性,所以只有当环路带宽⊙。满足 o。<1/10om时,连续时间模型才是有效的[1][2]。另外设计参数时,为了提高环路 稳定性,希望在。处的相位裕度最大,即对应了相位特性曲线的顶点,文献[3]给 出了设计最大相位裕量的方法。当开环参数设计好,由(2-2)就能得到闭环特性了。 H(s ∠H(S) PM 45° 0 0 0 W. p (a) (b) 图2.3开环传输函数的Bode图(a)幅度特性(b)相位特性 17
第二章 频率综合器的结构 17 H(s)是低通滤波器的传输函数;KV是 VCO 的压控增益;N 是分频器的分频比。 2.2.2 开环分析法 由于频率综合器是反馈系统,反馈系统可以用开环传输函数和反馈系数来表示闭 环传输函数。对于频率综合器的线性模型,其开环传输函数 Ho(s)为: ( ) ( ) P V o K K H s H s N s = (2-1) 其反馈系数是 1/N,则闭环传输函数 Hc(s)为: ( ) ( ) 1 () o c o NH s H s H s = + (2-2) 通常由于开环传输函数比较简单,而且易于分析,所以通常用开环特性分析替代闭 环特性分析。对于典型的二阶环路滤波器,即 ( ) ( ) z p s H s s s ω ω + = + (2-3) 其开环传输函数 Ho(s)的 Bode 图如图 2.3 所示,其中开环增益为 0 dB 的频率点 ωc 称为环路带宽;在 ωc 处的开环相位也被称为相位裕度。通过对开环传输函数的环路 带宽和相位裕度的设计可以方便的得到环路参数。值得注意的是,这里的模型是连 续时间模型,而实际的环路具有离散的特性,所以只有当环路带宽 ωc 满足 1/10 ωc in < ω 时,连续时间模型才是有效的[1][2]。另外设计参数时,为了提高环路 稳定性,希望在 ωc 处的相位裕度最大,即对应了相位特性曲线的顶点,文献[3]给 出了设计最大相位裕量的方法。当开环参数设计好,由(2-2)就能得到闭环特性了。 45o ωz ωc ω p Phase (deg) PM ( ) ∠H s o ωz ω p ωc Gain (dB) 0 ( ) H s o (a) (b) 图 2.3 开环传输函数的 Bode 图 (a)幅度特性 (b)相位特性

复旦大学博士学位论文 2.3频率综合器中的噪声 频率综合器的一个重要指标就是相位噪声,而相位噪声的来源就是频率综合器中 的各个模块。图2.4是相位噪声的线性模型,在这里共有五处噪声注入点,其来源 分别是: 1:输入参考时钟的相位噪声、分频器的输出等效相位噪声: 2:鉴相器和电荷泵的输出等效噪声: 3:环路滤波器的输出等效噪声: n4:VCO的输出等效相位噪声: 5:分频器的输入等效噪声、或其他的注入噪声: 这些噪声源都会传输到输出,但是它们的传输函数不同,其闭环传输函数的幅频特 性如图2.5所示,从图2.5中可以看到: 1)n1,n2和ns的传输函数是低通的:n3是带通的:n4是高通的:而且其共同的 截止频率正比于环路带宽。 2)n1,2,n3的通带增益是与分频系数N成正比的;而n4,n5的通带增益是1, 与N无关。 ni n2 n3 n4 LPF VCO H(s) Kv/S ÷N n5 图2.4频率综合器的噪声模型 IH2 lHn4l 7 N/KP 图2.5闭环噪声幅度传输函数的Bode图 18
复旦大学博士学位论文 18 2.3 频率综合器中的噪声 频率综合器的一个重要指标就是相位噪声,而相位噪声的来源就是频率综合器中 的各个模块。图 2.4 是相位噪声的线性模型,在这里共有五处噪声注入点,其来源 分别是: n1:输入参考时钟的相位噪声、分频器的输出等效相位噪声; n2:鉴相器和电荷泵的输出等效噪声; n3:环路滤波器的输出等效噪声; n4:VCO 的输出等效相位噪声; n5:分频器的输入等效噪声、或其他的注入噪声; 这些噪声源都会传输到输出,但是它们的传输函数不同,其闭环传输函数的幅频特 性如图 2.5 所示,从图 2.5 中可以看到: 1) n1,n2 和 n5 的传输函数是低通的;n3 是带通的;n4 是高通的;而且其共同的 截止频率正比于环路带宽。 2) n1,n2,n3的通带增益是与分频系数 N 成正比的;而 n4,n5 的通带增益是 1, 与 N 无关。 H(s) LPF VCO φin φvco KV/s ÷N KP n1 n2 n3 n4 n5 图 2.4 频率综合器的噪声模型 N N/KP 1 ∝ N 1 1 | | Hn 2 | | Hn 3 | | Hn 4 | | Hn 5 | | Hn 图 2.5 闭环噪声幅度传输函数的 Bode 图
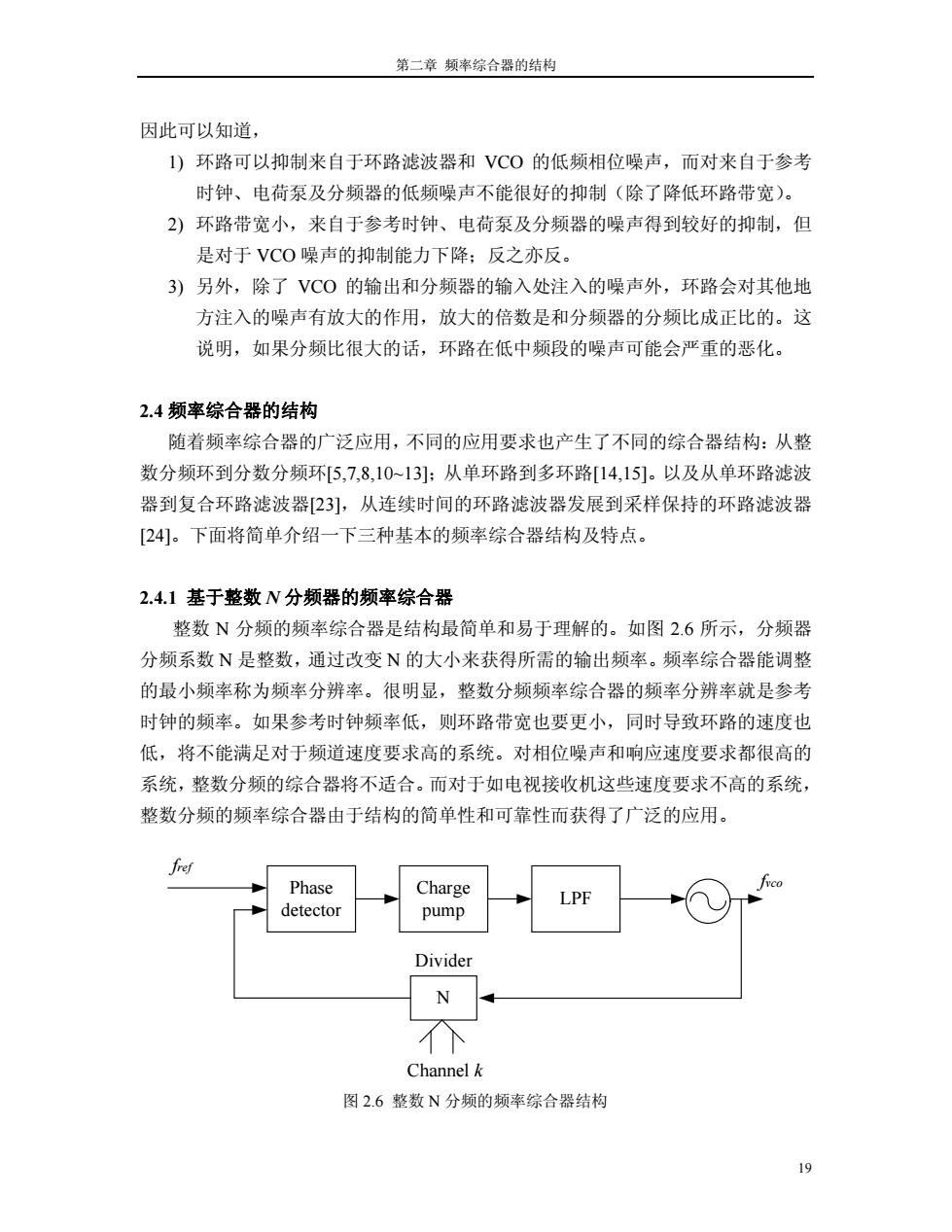
第二章频率综合器的结构 因此可以知道, 1)环路可以抑制来自于环路滤波器和VCO的低频相位噪声,而对来自于参考 时钟、电荷泵及分频器的低频噪声不能很好的抑制(除了降低环路带宽)。 2)环路带宽小,来自于参考时钟、电荷泵及分频器的噪声得到较好的抑制,但 是对于VCO噪声的抑制能力下降:反之亦反。 3)另外,除了VCO的输出和分频器的输入处注入的噪声外,环路会对其他地 方注入的噪声有放大的作用,放大的倍数是和分频器的分频比成正比的。这 说明,如果分频比很大的话,环路在低中频段的噪声可能会严重的恶化。 2.4频率综合器的结构 随着频率综合器的广泛应用,不同的应用要求也产生了不同的综合器结构:从整 数分频环到分数分频环5,7,8,10~13]:从单环路到多环路[14,15]。以及从单环路滤波 器到复合环路滤波器23],从连续时间的环路滤波器发展到采样保持的环路滤波器 [24]。下面将简单介绍一下三种基本的频率综合器结构及特点。 2.4.1基于整数N分频器的频率综合器 整数N分频的频率综合器是结构最简单和易于理解的。如图2.6所示,分频器 分频系数N是整数,通过改变N的大小来获得所需的输出频率。频率综合器能调整 的最小频率称为频率分辨率。很明显,整数分频频率综合器的频率分辨率就是参考 时钟的频率。如果参考时钟频率低,则环路带宽也要更小,同时导致环路的速度也 低,将不能满足对于频道速度要求高的系统。对相位噪声和响应速度要求都很高的 系统,整数分频的综合器将不适合。而对于如电视接收机这些速度要求不高的系统, 整数分频的频率综合器由于结构的简单性和可靠性而获得了广泛的应用。 fref Phase Charge LPF detector pump Divider N Channel k 图2.6整数N分频的频率综合器结构 19
第二章 频率综合器的结构 19 因此可以知道, 1) 环路可以抑制来自于环路滤波器和 VCO 的低频相位噪声,而对来自于参考 时钟、电荷泵及分频器的低频噪声不能很好的抑制(除了降低环路带宽)。 2) 环路带宽小,来自于参考时钟、电荷泵及分频器的噪声得到较好的抑制,但 是对于 VCO 噪声的抑制能力下降;反之亦反。 3) 另外,除了 VCO 的输出和分频器的输入处注入的噪声外,环路会对其他地 方注入的噪声有放大的作用,放大的倍数是和分频器的分频比成正比的。这 说明,如果分频比很大的话,环路在低中频段的噪声可能会严重的恶化。 2.4 频率综合器的结构 随着频率综合器的广泛应用,不同的应用要求也产生了不同的综合器结构:从整 数分频环到分数分频环[5,7,8,10~13];从单环路到多环路[14,15]。以及从单环路滤波 器到复合环路滤波器[23],从连续时间的环路滤波器发展到采样保持的环路滤波器 [24]。下面将简单介绍一下三种基本的频率综合器结构及特点。 2.4.1 基于整数 N 分频器的频率综合器 整数 N 分频的频率综合器是结构最简单和易于理解的。如图 2.6 所示,分频器 分频系数 N 是整数,通过改变 N 的大小来获得所需的输出频率。频率综合器能调整 的最小频率称为频率分辨率。很明显,整数分频频率综合器的频率分辨率就是参考 时钟的频率。如果参考时钟频率低,则环路带宽也要更小,同时导致环路的速度也 低,将不能满足对于频道速度要求高的系统。对相位噪声和响应速度要求都很高的 系统,整数分频的综合器将不适合。而对于如电视接收机这些速度要求不高的系统, 整数分频的频率综合器由于结构的简单性和可靠性而获得了广泛的应用。 Phase detector Charge pump LPF N Divider Channel k fref fvco 图 2.6 整数 N 分频的频率综合器结构
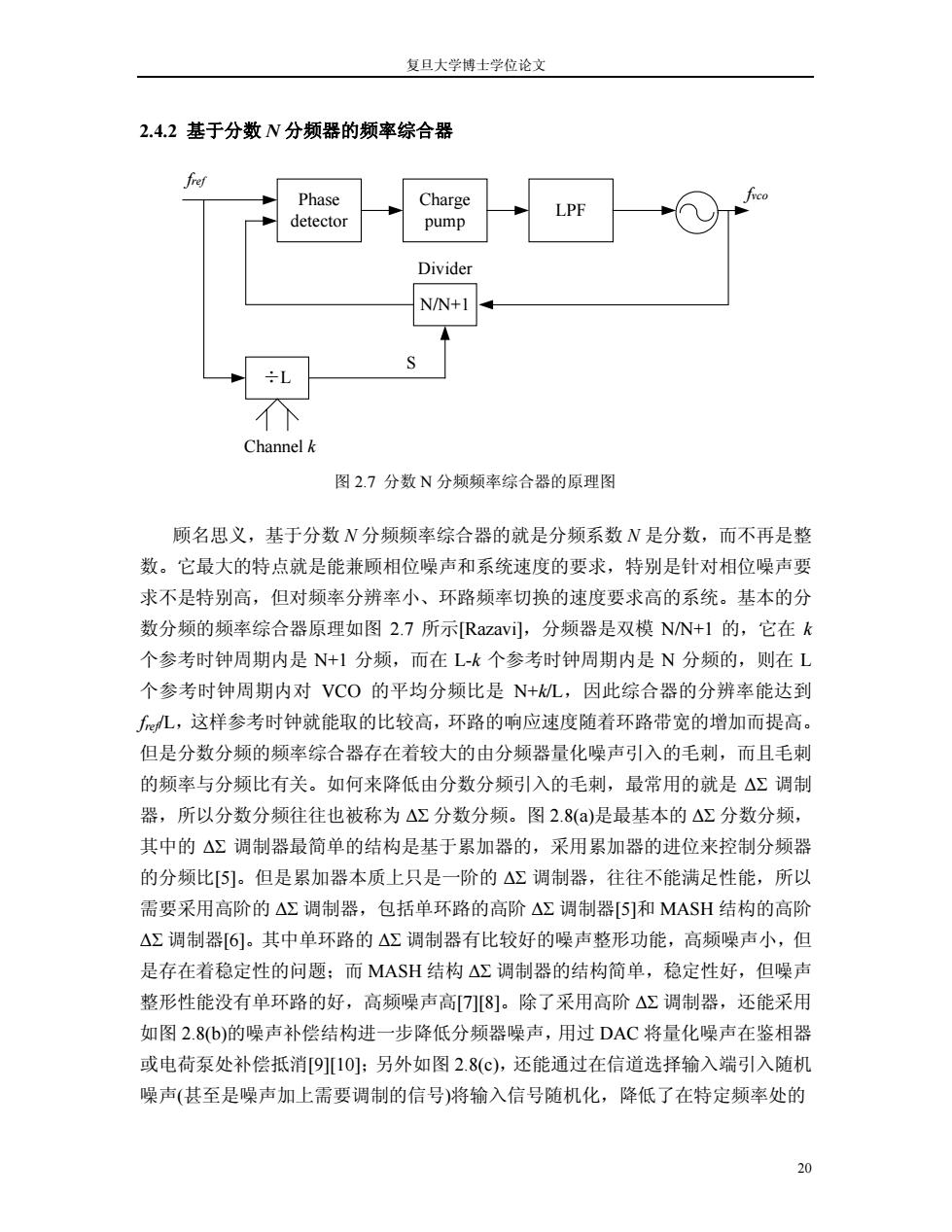
复旦大学博士学位论文 2.4.2基于分数N分频器的频率综合器 fref Phase Charge LPF detector pump Divider N/N+ Channel k 图2.7分数N分频频率综合器的原理图 顾名思义,基于分数N分频频率综合器的就是分频系数N是分数,而不再是整 数。它最大的特点就是能兼顾相位噪声和系统速度的要求,特别是针对相位噪声要 求不是特别高,但对频率分辨率小、环路频率切换的速度要求高的系统。基本的分 数分频的频率综合器原理如图2.7所示Razavi],分频器是双模NN+1的,它在k 个参考时钟周期内是N+1分频,而在Lk个参考时钟周期内是N分频的,则在L 个参考时钟周期内对VCO的平均分频比是N+kL,因此综合器的分辨率能达到 fL,这样参考时钟就能取的比较高,环路的响应速度随着环路带宽的增加而提高。 但是分数分频的频率综合器存在着较大的由分频器量化噪声引入的毛刺,而且毛刺 的频率与分频比有关。如何来降低由分数分频引入的毛刺,最常用的就是△Σ调制 器,所以分数分频往往也被称为△Σ分数分频。图2.8()是最基本的△Σ分数分频, 其中的△Σ调制器最简单的结构是基于累加器的,采用累加器的进位来控制分频器 的分频比[5]。但是累加器本质上只是一阶的△Σ调制器,往往不能满足性能,所以 需要采用高阶的△Σ调制器,包括单环路的高阶△Σ调制器[5]和MASH结构的高阶 △Σ调制器[6]。其中单环路的△Σ调制器有比较好的噪声整形功能,高频噪声小,但 是存在着稳定性的问题:而MASH结构△Σ调制器的结构简单,稳定性好,但噪声 整形性能没有单环路的好,高频噪声高[7[8]。除了采用高阶△Σ调制器,还能采用 如图2.8(b)的噪声补偿结构进一步降低分频器噪声,用过DAC将量化噪声在鉴相器 或电荷泵处补偿抵消[9[10]:另外如图2.8(©),还能通过在信道选择输入端引入随机 噪声(甚至是噪声加上需要调制的信号)将输入信号随机化,降低了在特定频率处的 20
复旦大学博士学位论文 20 2.4.2 基于分数 N 分频器的频率综合器 顾名思义,基于分数 N 分频频率综合器的就是分频系数 N 是分数,而不再是整 数。它最大的特点就是能兼顾相位噪声和系统速度的要求,特别是针对相位噪声要 求不是特别高,但对频率分辨率小、环路频率切换的速度要求高的系统。基本的分 数分频的频率综合器原理如图 2.7 所示[Razavi],分频器是双模 N/N+1 的,它在 k 个参考时钟周期内是 N+1 分频,而在 L-k 个参考时钟周期内是 N 分频的,则在 L 个参考时钟周期内对 VCO 的平均分频比是 N+k/L,因此综合器的分辨率能达到 fref/L,这样参考时钟就能取的比较高,环路的响应速度随着环路带宽的增加而提高。 但是分数分频的频率综合器存在着较大的由分频器量化噪声引入的毛刺,而且毛刺 的频率与分频比有关。如何来降低由分数分频引入的毛刺,最常用的就是 ∆Σ 调制 器,所以分数分频往往也被称为 ∆Σ 分数分频。图 2.8(a)是最基本的 ∆Σ 分数分频, 其中的 ∆Σ 调制器最简单的结构是基于累加器的,采用累加器的进位来控制分频器 的分频比[5]。但是累加器本质上只是一阶的 ∆Σ 调制器,往往不能满足性能,所以 需要采用高阶的 ∆Σ 调制器,包括单环路的高阶 ∆Σ 调制器[5]和 MASH 结构的高阶 ∆Σ 调制器[6]。其中单环路的 ∆Σ 调制器有比较好的噪声整形功能,高频噪声小,但 是存在着稳定性的问题;而 MASH 结构 ∆Σ 调制器的结构简单,稳定性好,但噪声 整形性能没有单环路的好,高频噪声高[7][8]。除了采用高阶 ∆Σ 调制器,还能采用 如图 2.8(b)的噪声补偿结构进一步降低分频器噪声,用过 DAC 将量化噪声在鉴相器 或电荷泵处补偿抵消[9][10];另外如图 2.8(c),还能通过在信道选择输入端引入随机 噪声(甚至是噪声加上需要调制的信号)将输入信号随机化,降低了在特定频率处的 Phase detector Charge pump LPF N/N+1 Divider ÷L Channel k fref fvco S 图 2.7 分数 N 分频频率综合器的原理图
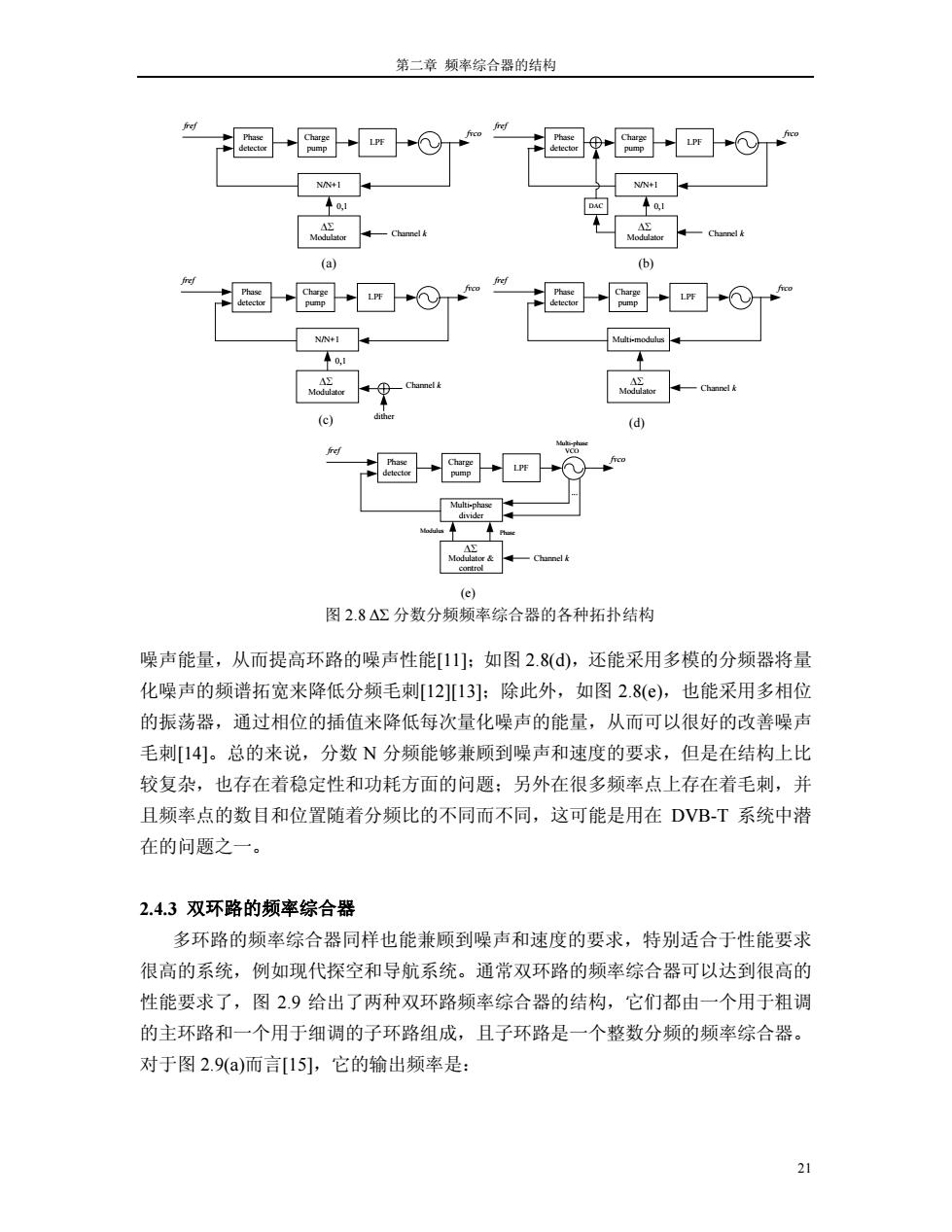
第二章频率综合器的结构 N/N+I N/N+I ↑0,1 AE Modulator 一Channel Modulator (a) (b) 胸w→①T N/N+I Multi-modulus 年0,1 Channel Modulator 一Channel (c) (d) Phase Multi-phase Channel k (e) 图2.8△Σ分数分频频率综合器的各种拓扑结构 噪声能量,从而提高环路的噪声性能[11]:如图2.8(d,还能采用多模的分频器将量 化噪声的频谱拓宽来降低分频毛刺[12][13]:除此外,如图2.8(©),也能采用多相位 的振荡器,通过相位的插值来降低每次量化噪声的能量,从而可以很好的改善噪声 毛刺[14]。总的来说,分数N分频能够兼顾到噪声和速度的要求,但是在结构上比 较复杂,也存在着稳定性和功耗方面的问题;另外在很多频率点上存在着毛刺,并 且频率点的数目和位置随着分频比的不同而不同,这可能是用在DVB-T系统中潜 在的问题之一。 2.4.3双环路的频率综合器 多环路的频率综合器同样也能兼顾到噪声和速度的要求,特别适合于性能要求 很高的系统,例如现代探空和导航系统。通常双环路的频率综合器可以达到很高的 性能要求了,图29给出了两种双环路频率综合器的结构,它们都由一个用于粗调 的主环路和一个用于细调的子环路组成,且子环路是一个整数分频的频率综合器。 对于图2.9(a)而言[15],它的输出频率是: 21
第二章 频率综合器的结构 21 噪声能量,从而提高环路的噪声性能[11];如图 2.8(d),还能采用多模的分频器将量 化噪声的频谱拓宽来降低分频毛刺[12][13];除此外,如图 2.8(e),也能采用多相位 的振荡器,通过相位的插值来降低每次量化噪声的能量,从而可以很好的改善噪声 毛刺[14]。总的来说,分数 N 分频能够兼顾到噪声和速度的要求,但是在结构上比 较复杂,也存在着稳定性和功耗方面的问题;另外在很多频率点上存在着毛刺,并 且频率点的数目和位置随着分频比的不同而不同,这可能是用在 DVB-T 系统中潜 在的问题之一。 2.4.3 双环路的频率综合器 多环路的频率综合器同样也能兼顾到噪声和速度的要求,特别适合于性能要求 很高的系统,例如现代探空和导航系统。通常双环路的频率综合器可以达到很高的 性能要求了,图 2.9 给出了两种双环路频率综合器的结构,它们都由一个用于粗调 的主环路和一个用于细调的子环路组成,且子环路是一个整数分频的频率综合器。 对于图 2.9(a)而言[15],它的输出频率是: Phase detector Charge pump LPF fref fvco N/N+1 Channel k ∆Σ Modulator 0,1 Phase detector Charge pump LPF fref fvco N/N+1 Channel k ∆Σ Modulator DAC 0,1 (a) (b) Phase detector Charge pump LPF Multi-phase divider fref fvco Channel k ∆Σ Modulator & control Multi-phase VCO ... Modulus Phase (e) Phase detector Charge pump LPF fref fvco N/N+1 ∆Σ Channel k Modulator 0,1 (c) dither Phase detector Charge pump LPF Multi-modulus fref fvco Channel k ∆Σ Modulator (d) 图 2.8 ∆Σ 分数分频频率综合器的各种拓扑结构