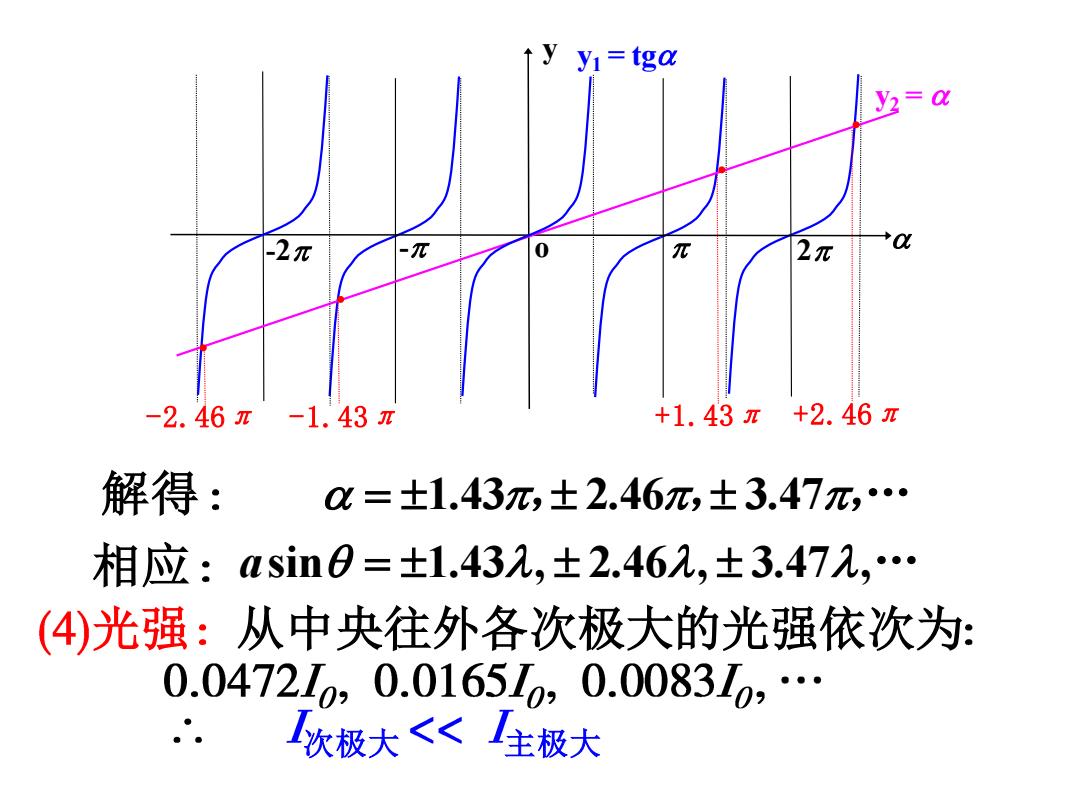
yy=tga 】.1 -2.46π-1.43π +1.43π+2.46π 解得: a=±1.43π,±2.46π,±3.47元,… 相应:asin0=±1.432,±2.46,±3.472,… (4)光强:从中央往外各次极大的光强依次为: 0.0472L,0.016510,0.0083L0,… 次极大<生极大
解得 = 1.43, 2.46, 3.47, … 相应 asin = 1.43, 2.46, 3.47, … 光强 从中央往外各次极大的光强依次为 次极大 主极大 -2.46π o -2 - 2 y y1 = tg y2 = -1.43π +1.43π +2.46π · · · ·
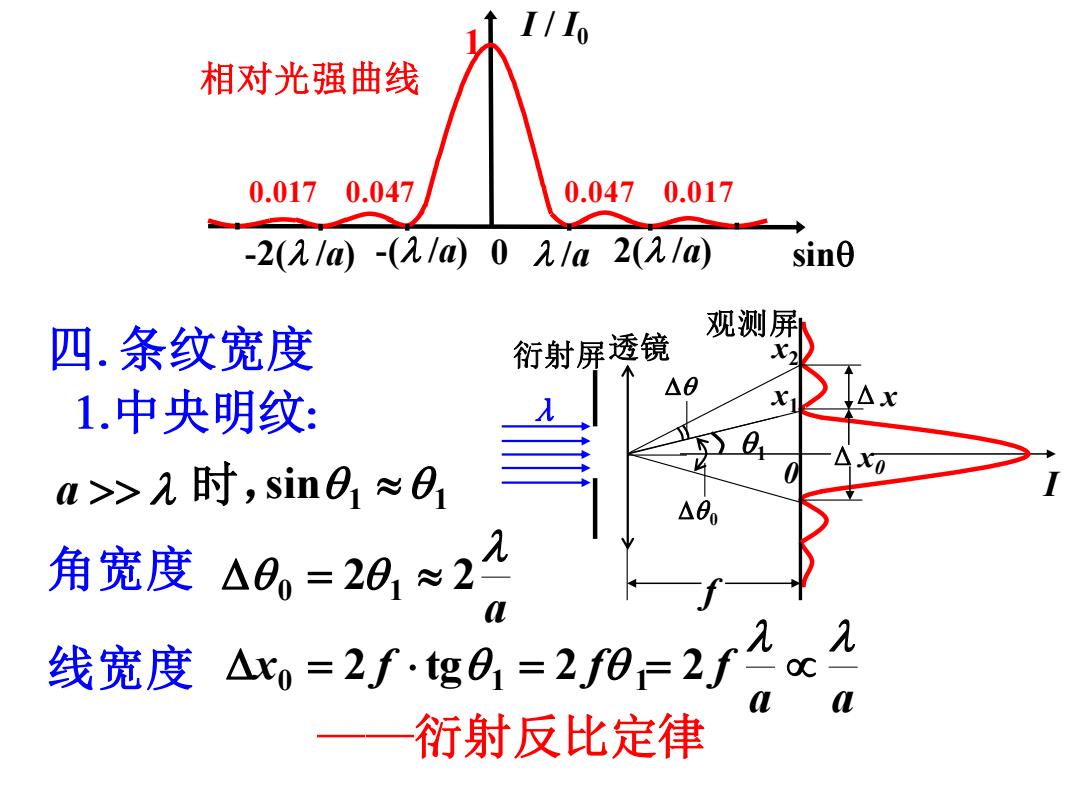
I/I 相对光强曲线 0.0170.047 0.0470.017 -2(21@-(21@0元1a2(21a sin 四.条纹宽度 观测屏 衍射屏透镜 △8 1.中央明纹: a>>时,sin01≈01 角宽度△6,=28,≈22 线宽度A,=2ftg0,=2f8=2f2x2 aa 衍射反比定律
-2( /a) -( /a) /a 2( /a) sin 0.047 0.017 1 I / I0 0 相对光强曲线 0.017 0.047 四 条纹宽度 中央明纹 λ Δx I 0 x1 衍射屏透镜 x2 观测屏 Δx0 f 1 0 1 1 a 时, sin 角宽度 a 0 = 2 1 2 线宽度 a a x f f f 0 = 2 tg 1 = 2 1= 2 衍射反比定律

2.其他明纹(次极大) Ac≈i-)Ax, a 2 3.波长对条纹宽度的影响 △roc1波长越长, 条纹宽度越宽 4.缝宽变化对条纹的影响 Ar=Ax=f 24 缝宽越小,条纹宽度越宽 ↑1 当→0 时, sine 屏幕是一片亮
其他明纹 次极大 0 2 1 x a f x = 波长对条纹宽度的影响 缝宽变化对条纹的影响 x 波长越长,条纹宽度越宽 a x x f = 0 = 2 1 缝宽越小,条纹宽度越宽 当 → 0 时, a 屏幕是一片亮 I 0 sin