§3感生电动势感生电场 当回路1中电流发生变化时,在回路 2中出现感应电动势。 BATTERY 1020300 电池 回路1 回路2 产生感应电动势的非静电力是什么?
当回路 1中电流发生变化时,在回路 2中出现感应电动势。 产生感应电动势的非静电力是什么? 回路2 电池 BATTERY G 回路1 §3 感生电动势 感生电场
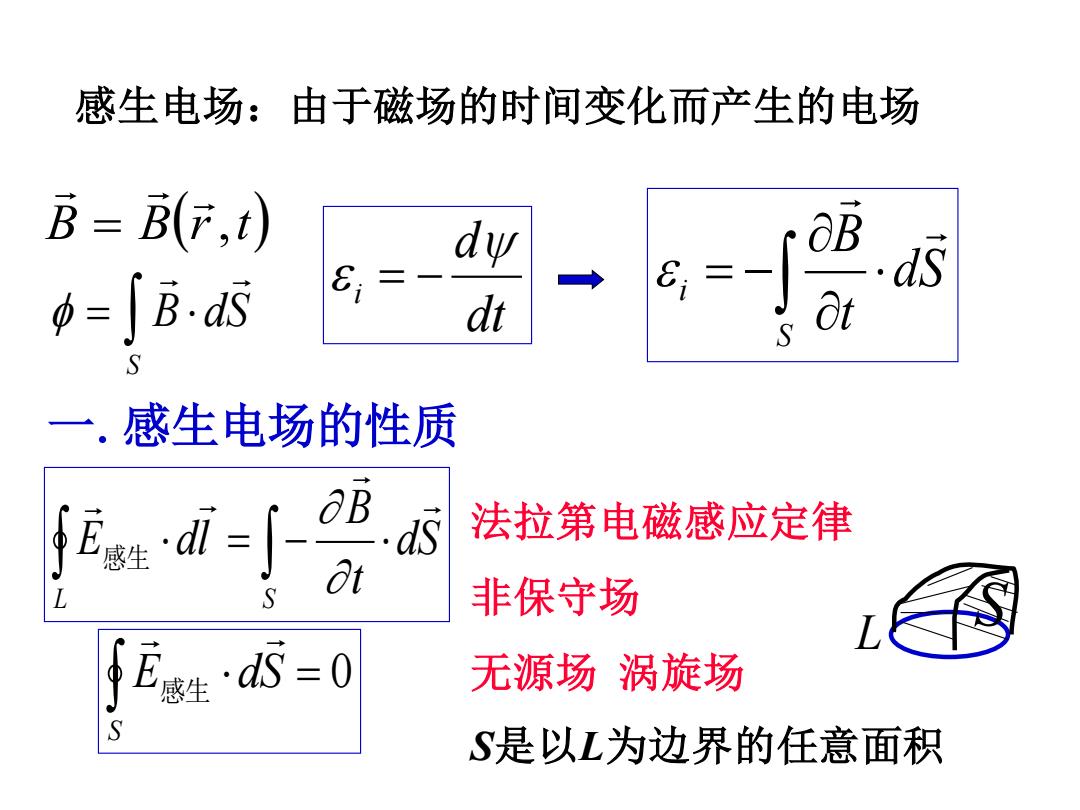
感生电场:由于磁场的时间变化而产生的电场 B=(厅,t) ds p=∫BS dt 一.感生电场的性质 6B 法拉第电磁感应定律 非保守场 E生=0 无源场涡旋场 S是以L为边界的任意面积
( ) B = B r,t = B dS S 一.感生电场的性质 dS t B E dl L S = − 感生 = 0 S E dS 感生 法拉第电磁感应定律 非保守场 无源场 涡旋场 S是以L为边界的任意面积L S dt d i = − = − S i dS t B 感生电场:由于磁场的时间变化而产生的电场
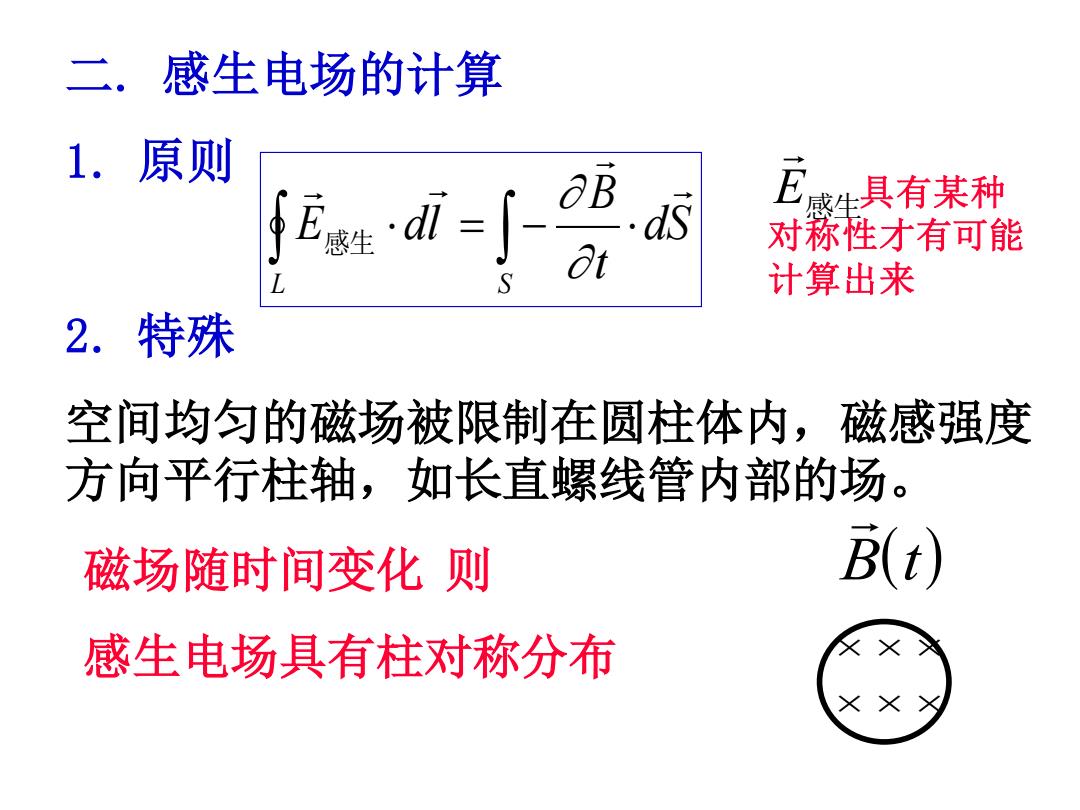
二. 感生电场的计算 1.原则 Ew姓d-∫ dS a 尼感生具有某种 对称性才有可能 计算出来 2.特殊 空间均匀的磁场被限制在圆柱体内,磁感强度 方向平行柱轴,如长直螺线管内部的场。 磁场随时间变化则 (t) 感生电场具有柱对称分布 ××
二. 感生电场的计算 1. 原则 dS t B E dl L S = − 感生 2. 特殊 空间均匀的磁场被限制在圆柱体内,磁感强度 方向平行柱轴,如长直螺线管内部的场。 磁场随时间变化 则 感生电场具有柱对称分布 ( ) B t 具有某种 对称性才有可能 计算出来 E感生
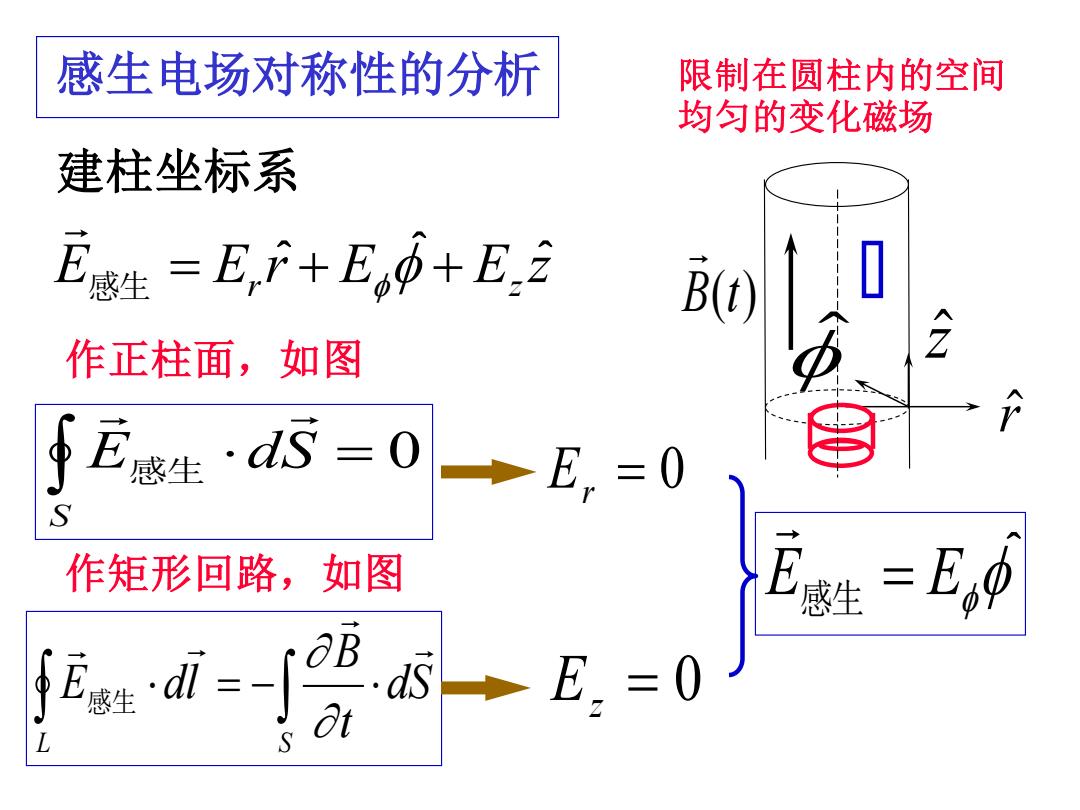
感生电场对称性的分析 限制在圆柱内的空间 均匀的变化磁场 建柱坐标系 Es生=E,F+E,0+E,2 B() 作正柱面,如图 ∮E感生·dS =0 E.=0 作矩形回路,如图 =E0 f Eaa'dl=- E.=0
r z 作正柱面,如图 = 0 E dS S 感生 Er = 0 dS t B E dl L S = − 感生 Ez = 0 感生电场对称性的分析 B(t) 限制在圆柱内的空间 均匀的变化磁场 建柱坐标系 E E r E E z 感生 = r + + z ^ ^ ^ 作矩形回路,如图 E感生 = E ^

3.特殊情况下感生电场的计算 空间均匀的磁场限制在半径为R 的圆柱内,B的方向平行柱轴 且有 dB dt 求:E感生分布 解:设场点距轴心为r,根据对称性,取以 o为心,过场点的圆周环路L dB ∫E姓·d=Ew姓2πr 由法拉第电 磁感应定律 =-S dt
3. 特殊情况下感生电场的计算 空间均匀的磁场限制在半径为 R 的圆柱内, 求: 感生 E 分布 解:设场点距轴心为r ,根据对称性,取以 o为心,过场点的圆周环路 L E dl E r L 感生 = 感生 2 B • 0 L r dt dB = −S 由法拉第电 磁感应定律 B 的方向平行柱轴 c dt dB 且有 =