
§3高斯定理 一.电力线 用一族空间曲线形象描述场强分布 通常把这些曲线称为电场线(electric field line)或电力线(electric line of force) 1.规定 方向:力线上每一点的切线方向; 大小:在电场中任一点,取一垂直于该点场强 方向的面积元,则通过单位面积的电力线数目, 等于该点场强的量值
§3 高斯定理 一.电力线 用一族空间曲线形象描述场强分布 通常把这些曲线称为电场线(electric field line)或电力线 (electric line of force) 1.规定 方向:力线上每一点的切线方向; 大小:在电场中任一点,取一垂直于该点场强 方向的面积元,则通过单位面积的电力线数目, 等于该点场强的量值

dΦ 匀强电场元 E ds dΦ=Eds, 若面积元不垂直电场强度, 电场强度与电力线条数、 面积元的 关系怎样? 由图可知通过ds和ds,电力线条数相同 ds dsn d中=Eds,=Eds cos e→ dφ=E·dS
E d dS = ⊥ dS ds E dS⊥ d = Eds⊥ 若面积元不垂直电场强度, 电场强度与电力线条数、面积元的 关系怎样? 由图可知 通过 ds 和 ds⊥ 电力线条数相同 d = Eds⊥ E ds = dsn ^ = Edscos d = E dS 匀强电场

2.电力线的性质 1)电力线起始于正电荷(或无穷远处), 终止于负电荷,不会在没有电荷处中断; 2)两条电场线不会相交; 3)电力线不会形成闭合曲线。 之所以具有这些基本性质, 由静电场的基本性质和场的单值性决定的。 可用静电场的基本性质方程加以证明
2.电力线的性质 1)电力线起始于正电荷(或无穷远处), 终止于负电荷,不会在没有电荷处中断; 2)两条电场线不会相交; 3)电力线不会形成闭合曲线。 之所以具有这些基本性质, 由静电场的基本性质和场的单值性决定的。 可用静电场的基本性质方程加以证明
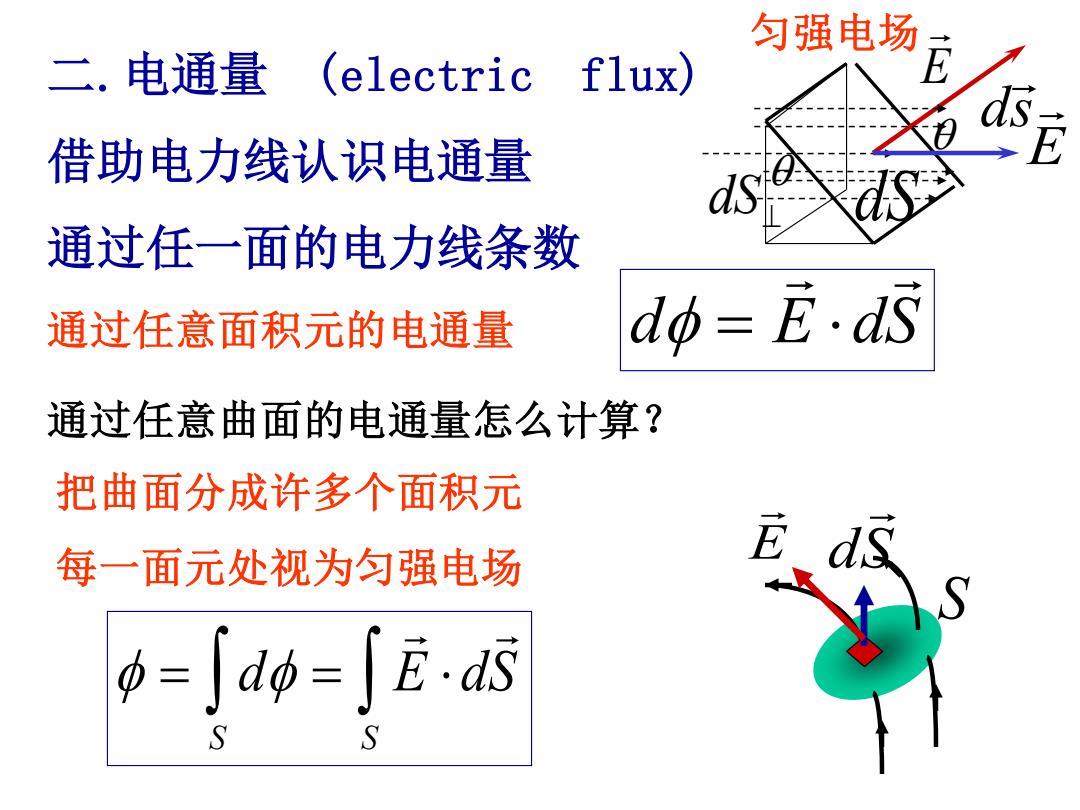
匀强电场 二.电通量(electric flux) 借助电力线认识电通量 通过任一面的电力线条数 通过任意面积元的电通量 d=E·dS 通过任意曲面的电通量怎么计算? 把曲面分成许多个面积元 每一面元处视为匀强电场 =「d0=「Ed
二.电通量 (electric flux) 借助电力线认识电通量 通过任一面的电力线条数 = = d E dS S S dS ds E dS⊥ E 匀强电场 d = E dS 通过任意面积元的电通量 通过任意曲面的电通量怎么计算? S 把曲面分成许多个面积元 每一面元处视为匀强电场 dS E
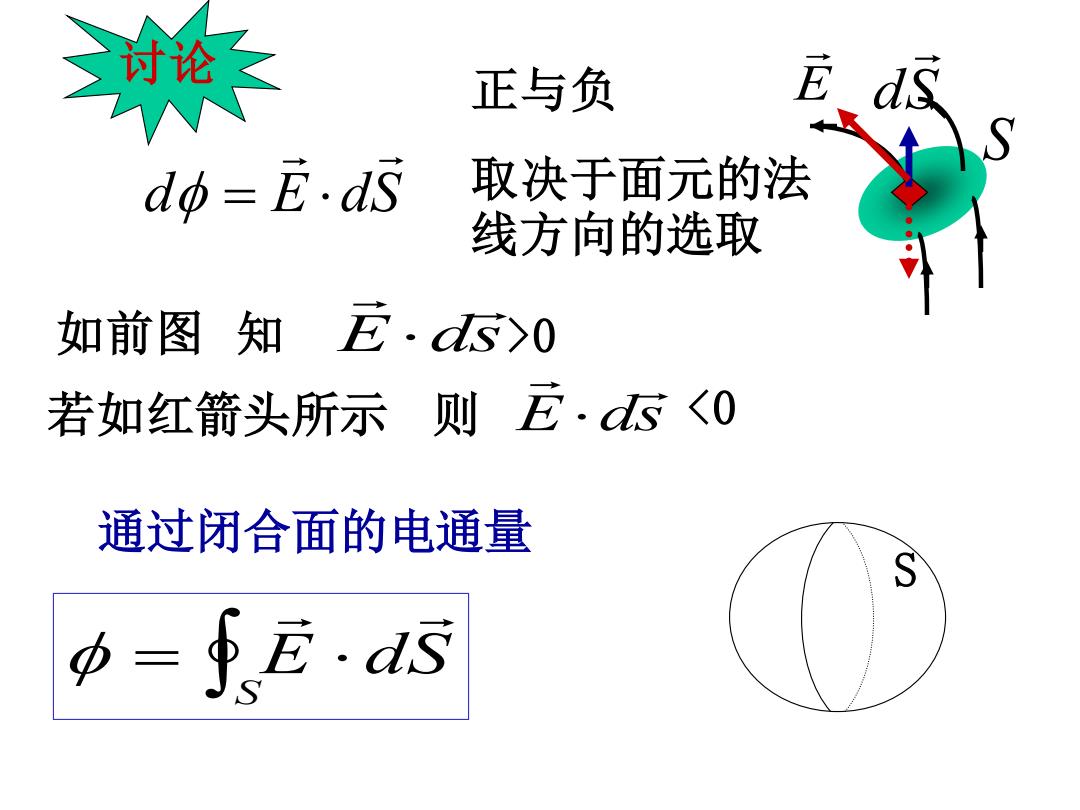
≥讨论 正与负 E dΦ=E,ds 取决于面元的法 线方向的选取 如前图知五.cd5>0 若如红箭头所示则E·d5〈0 通过闭合面的电通量
通过闭合面的电通量 = E dS S 讨论 d E dS = 正与负 取决于面元的法 线方向的选取 S dS E 如前图 知 E ds >0 若如红箭头所示 则 E ds <0 S