§4自感和互感 一、自感应 自感现象 由于回路自身电流的变化, 在回路中产生感应电动势的现象。 如果:回路几何形状、尺寸不变,周围无铁 磁性物质。 实验指出: Φ&I =L1 自感系数 单位:亨利(H)
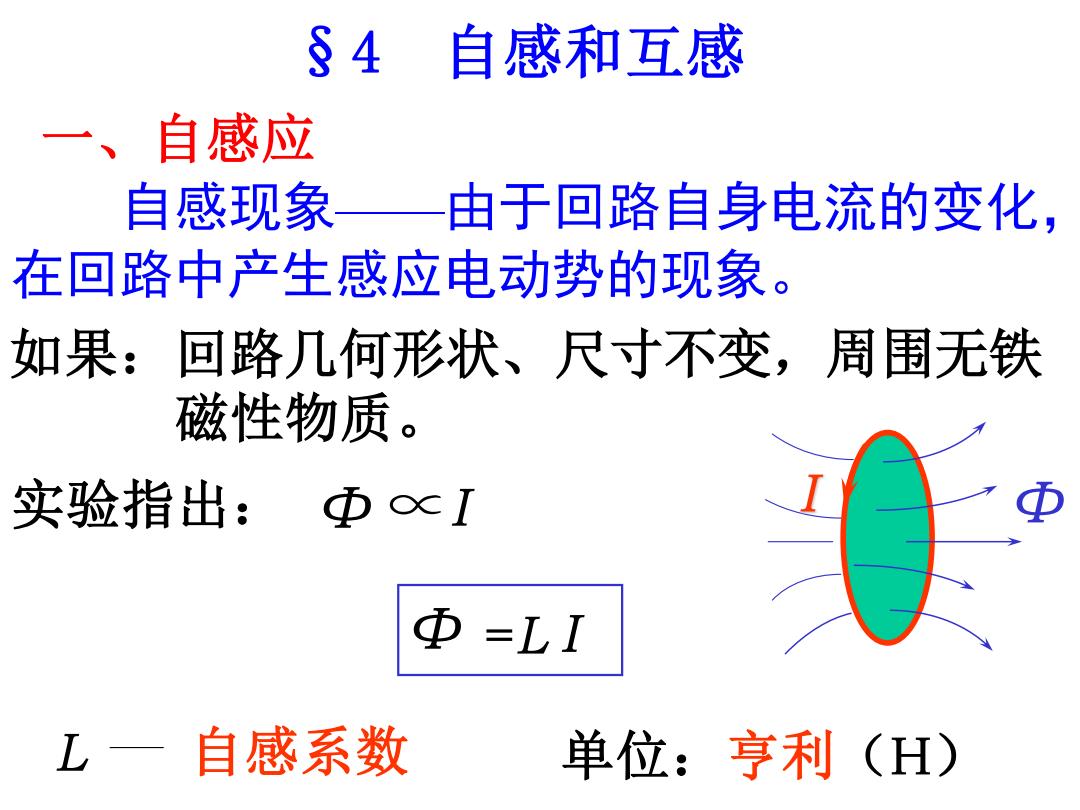
Φ =L I 如果:回路几何形状、尺寸不变,周围无铁 磁性物质。 L 自感系数 §4 自感和互感 自感现象——由于回路自身电流的变化, 在回路中产生感应电动势的现象。 实验指出: Φ ∝I I Φ 单位:亨利(H) 一、自感应

对于N匝线圈: Ψ=NΦ=LI 磁通链 L的意义:若I=1,则L=Ψ。自感系 数在数值上等于回路中通过单位电流时,通 过自身回路所包围面积的磁通链数
对于N 匝线圈: Ψ = NΦ =L I Ψ 磁通链 数在数值上等于回路中通过单位电流时,通 L 的意义:若 I = 1,则 L = Ψ 。自感系 过自身回路所包围面积的磁通链数

自感电动势: EL=-N =-d(NΦ) =-dΨ dt dt dt d(LD)--LdI-Idi dt dt dt 若回路几何形状、尺寸不变,周围无铁磁性 物质,则:股=0 自感电动势
自感电动势: d L = dt ( I ) = d dt L 0 若回路几何形状、尺寸不变,周围无铁磁性 自感电动势 Ψ = d dt ( ) = d NΦ dt N d = Φ dt ε L d dt L I d dt L = I 物质,则: ε L = d dt L I

E-品 讨论: 1.若:<0则e:>0e,与1方向相同 若:0则E.<0E与I方向相反 2.L的存在总是阻碍电流的变化,L是电 磁惯性的一种表现。 3.自感系数决定于回路的几何形状、尺寸 以及周围介质的磁导率
ε L = d dt L I 3. 自感系数决定于回路的几何形状、尺寸 讨论: d dt I 1. 若: < 0 则:ε L >0 > d dt I 若: 0 则:ε L<0 ε,L与 I 方向相反 ε,L 与 I 方向相同 2. L 的存在总是阻碍电流的变化,L 是电 磁惯性的一种表现。 以及周围介质的磁导率
例1求一无限长同轴传输线单位长度的 自感。已知:R1,R2 H- 2饥r B=HI 2元r o-日as=数1td Φ-fB.ds=ILR,dr 2rJR1r -n(R→i-中-1aR 2死 ==1n(B) 单位长度的自感为:L。=1=2玩 R
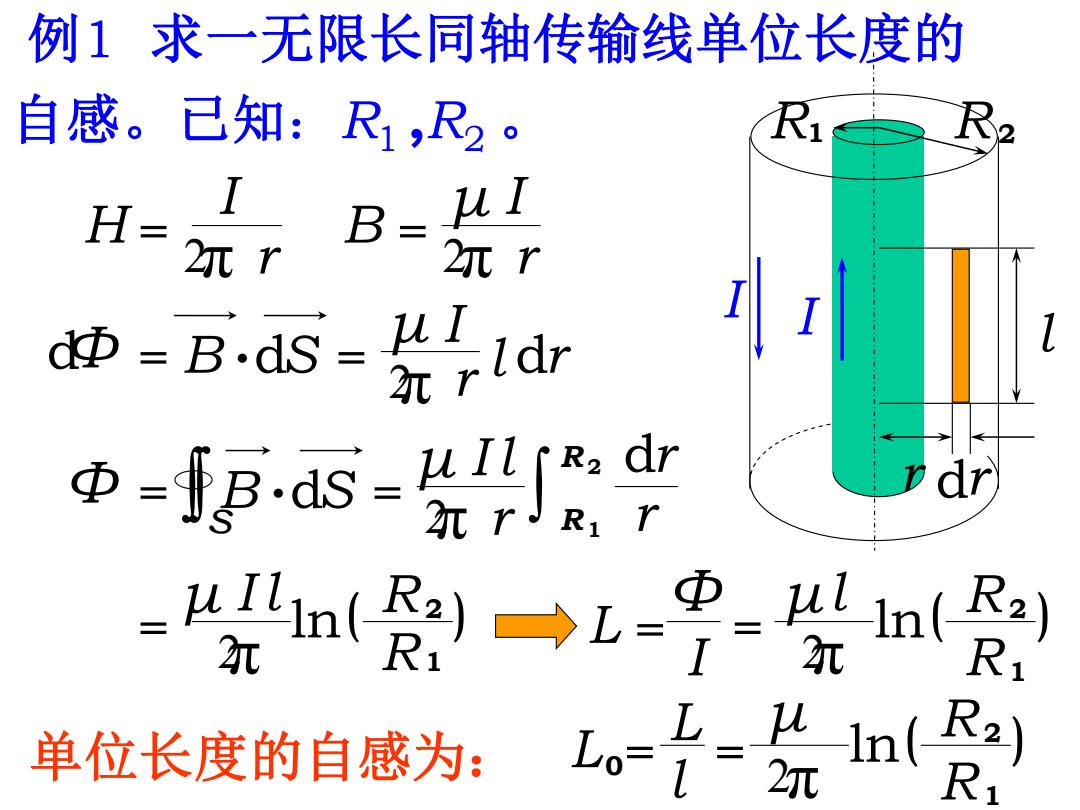
dΦ = B .dS 2π r H = I μ 2π r B = I π = l dr μ 2 r I μ π ( ) = 2 I l ln R1 R2 π L = ( ) μ 2 ln R1 R2 0 l L 单位长度的自感为: = 例1 求一无限长同轴传输线单位长度的 自感。已知:R1 ,R2 。 π R = μ 2 r I l 1 R 2 dr r Φ = B dS . s L π = μ ( ) 2 l ln R1 Φ R2 I = I I l r dr R1 R 2