
4.1组合逻辑电路的分析 Combinational Circuits Analysis Analysis Procedure 逻辑图→表达式→化简→真值表→逻辑功能 1.由给定的逻辑图逐级写出逻辑表达式; 2.化简逻辑表达式式,得出最简与或表达式; 化简方法:公式化简法和卡诺图法 3.列出真值表,分析真值表得到逻辑功能
1.由给定的逻辑图逐级写出逻辑表达式; 2.化简逻辑表达式式,得出最简与或表达式; 3.列出真值表,分析真值表得到逻辑功能。 化简方法:公式化简法和卡诺图法 逻辑图 表达式 化简 真值表 逻辑功能 Analysis Procedure 4.1 组合逻辑电路的分析 Combinational Circuits Analysis
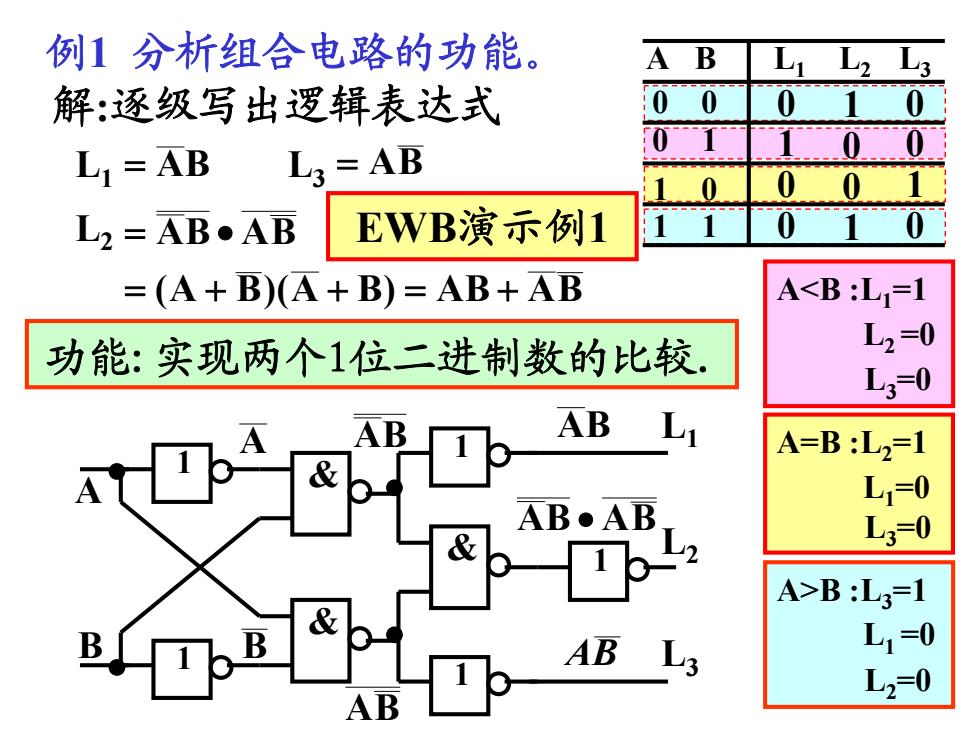
例1分析组合电路的功能。 A B 解:逐级写出逻辑表达式 0 0 L=AB L3=AB 0 0 L2=AB●AD EWB演示例1 =(A+B)(A+B)=AB+AB A<B:L=1 功能:实现两个1位二进制数的比较. L2=0 L3=0 AB AB A=B:L2=1 L1=0 AB●AB L3=0 1 A>B:L3=1 AB L1=0 L2=0 AB
A<B :L1 =1 L2 =0 L3 =0 A=B :L2 =1 L1 =0 L3 =0 A>B :L3 =1 L1 =0 L2 =0 例1 分析组合电路的功能。 1 & 1 1 1 1 & & • • • • A B L1 L3 L2 A B BA BA BA AB BABA 解:逐级写出逻辑表达式 L1 BA L3 BA L2 BABA BAAB)BA)(BA( 0 0 A B L1 L2 L3 0 1 1 0 1 1 0 1 0 1 0 0 0 0 1 0 1 0 功能:实现两个1位二进制数的比较. EWB演示例1
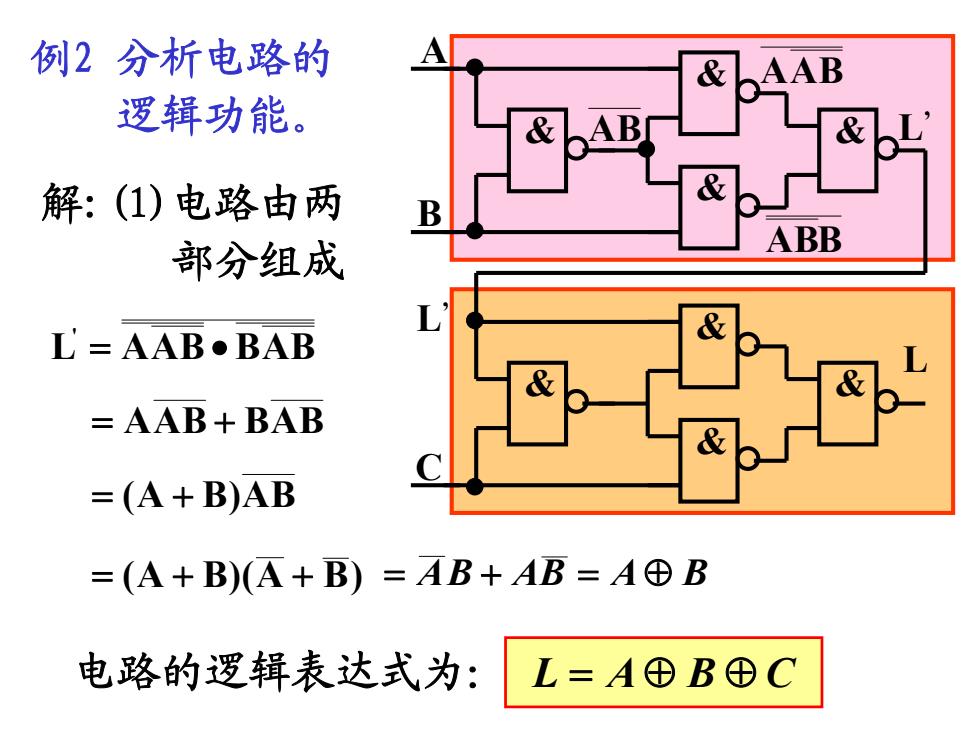
例2分析电路的 AAB 逻辑功能。 解:(1)电路由两 部分组成 ABB L E=AAB·BAB =AAB+BAB =(A+B)AB =(A+B)(A+B)=4B+AB=AB 电路的逻辑表达式为:L=A田B⊕C
L & L’ & & & & & & & A B C L’ 例2 分析电路的 逻辑功能。 解:(1)电路由两 部分组成 L AAB BAB ' AAB BAB (A B)AB (A B)(A B) AB AB A B AB AAB ABB 电路的逻辑表达式为: L A B C
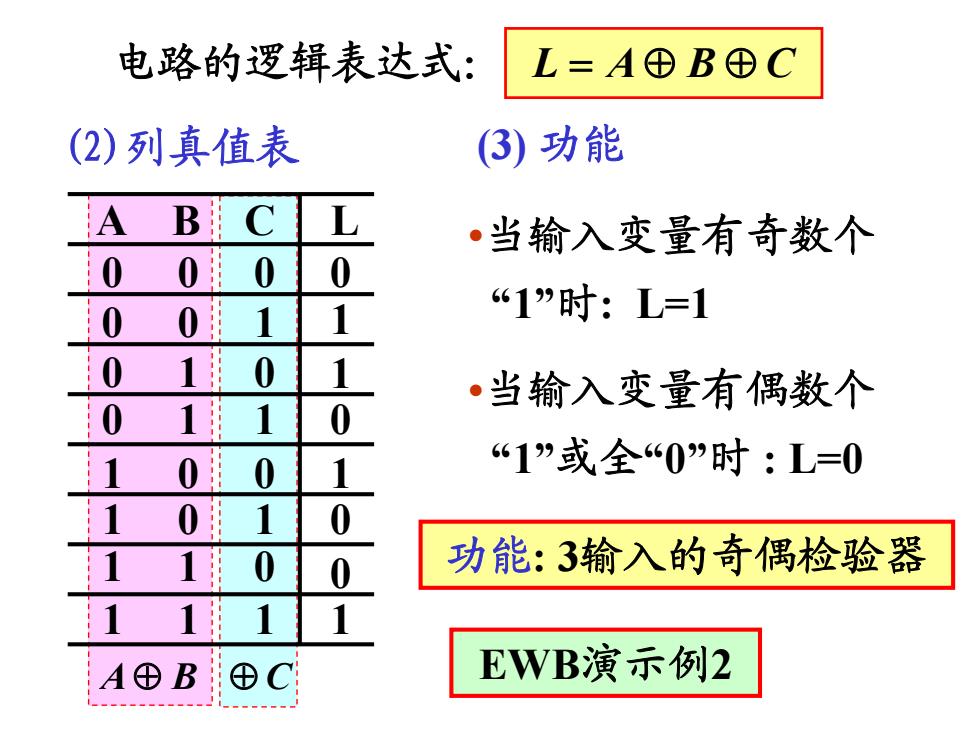
电路的逻辑表达式: L=A⊕B⊕C (2)列真值表 (3)功能 A B L ·当输入变量有奇数个 0 0 0 0 0 0 1 61”时:L=1 0 ·当输入变量有偶数个 0 1 “1”或全“0”时:L=0 0 0 功能:3输入的奇偶检验器 A⊕B ⊕C EWB演示例2
A B C 0 0 0 0 1 1 1 1 A B C L 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 •当输入变量有奇数个 “1”时: L=1 •当输入变量有偶数个 “1”或全“0”时 : L=0 (2)列真值表 (3) 功能 电路的逻辑表达式: L A CB 功能: 3输入的奇偶检验器 EWB演示例2
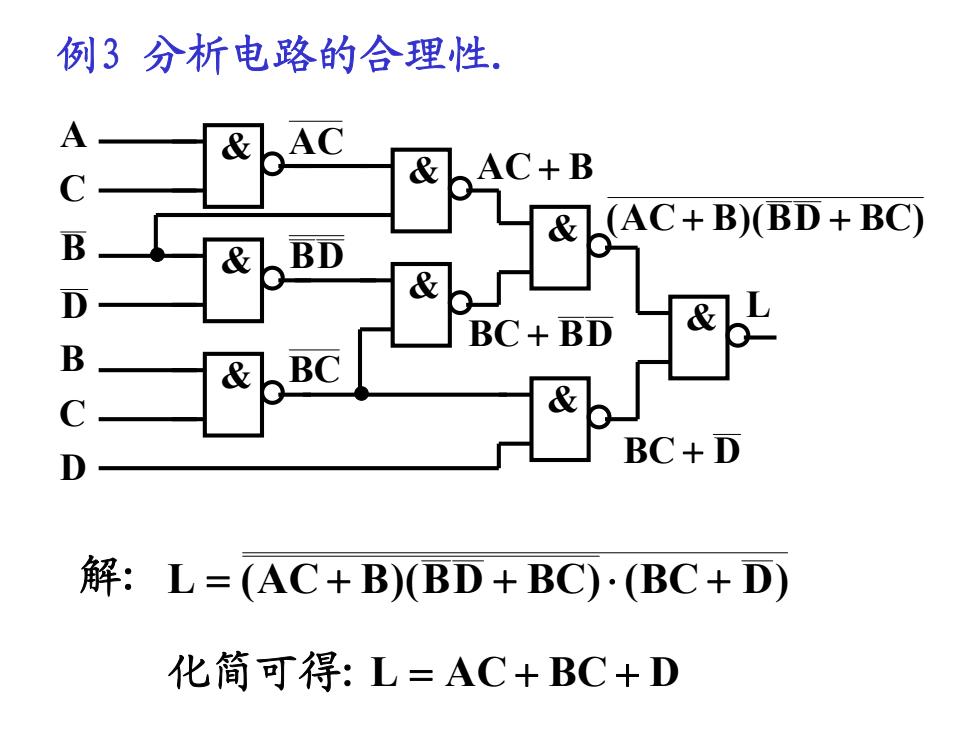
例3分析电路的合理性. A 。AC AC+B C & &AC+B)(BD+BC) B & BD D & BC+BD & B BC C & BC+D D 解:L=(AC+B)BD+BC)(BC+D) 化简可得:L=AC+BC+D
AC DB BC BAC DBBC DBC )BCDB)(BAC( & & & & & & & & A C B D B C D L 例3 分析电路的合理性. 解: )DBC()BCDB)(BAC(L 化简可得: DBCACL