
通常信道特性c(t)是一个复杂的函数,它可能包括各种 线性失真、非线性失真、交调失真、衰落等。同时由于信道 的迟延特性和损耗特性随时间作随机变化,故c)往往只能 用随机过程来描述。在我们实际使用的物理信道中,根据信 道传输函数C(o)的时变特性的不同可以分为两大类:一类是 C(@)基本不随时间变化,即信道对信号的影响是固定的或变 化极为缓慢的,这类信道称为恒定参量信道,简称恒参信道; 另一类信道是传输函数C(ω)随时间随机快变化,这类信道 称为随机参量信道,简称随参信道
通常信道特性c(t)是一个复杂的函数,它可能包括各种 线性失真、非线性失真、交调失真、衰落等。同时由于信道 的迟延特性和损耗特性随时间作随机变化,故c(t)往往只能 用随机过程来描述。在我们实际使用的物理信道中,根据信 道传输函数C(ω)的时变特性的不同可以分为两大类:一类是 C(ω)基本不随时间变化,即信道对信号的影响是固定的或变 化极为缓慢的,这类信道称为恒定参量信道,简称恒参信道; 另一类信道是传输函数C(ω)随时间随机快变化, 这类信道 称为随机参量信道,简称随参信道

在常用物理信道中,C(Q)的特性有三种典型形式。第一 种形式C(o)是常数,或在信号频带范围之内是常数。这种信 道可以用加性噪声信道数学模型来表示,如图3-3所示。 信号通过信道的输出为 r(t)=s,(t)+n(t)-cs;(t)+n(t) (3.1-4) 式中,c是信道衰减因子,通常可取c=1;n(t)是加性噪 声。由后几节分析我们将看到,加性噪声(t)通常是一种高 斯噪声,该信道模型通常称为加性高斯噪声信道
在常用物理信道中,C(ω)的特性有三种典型形式。第一 种形式C(ω)是常数,或在信号频带范围之内是常数。这种信 道可以用加性噪声信道数学模型来表示, 如图 3 - 3 所示。 信号通过信道的输出为 r(t)=so (t)+n(t)=csi (t)+n(t) (3.1 - 4) 式中, c是信道衰减因子, 通常可取c=1; n(t)是加性噪 声。由后几节分析我们将看到,加性噪声n(t)通常是一种高 斯噪声, 该信道模型通常称为加性高斯噪声信道
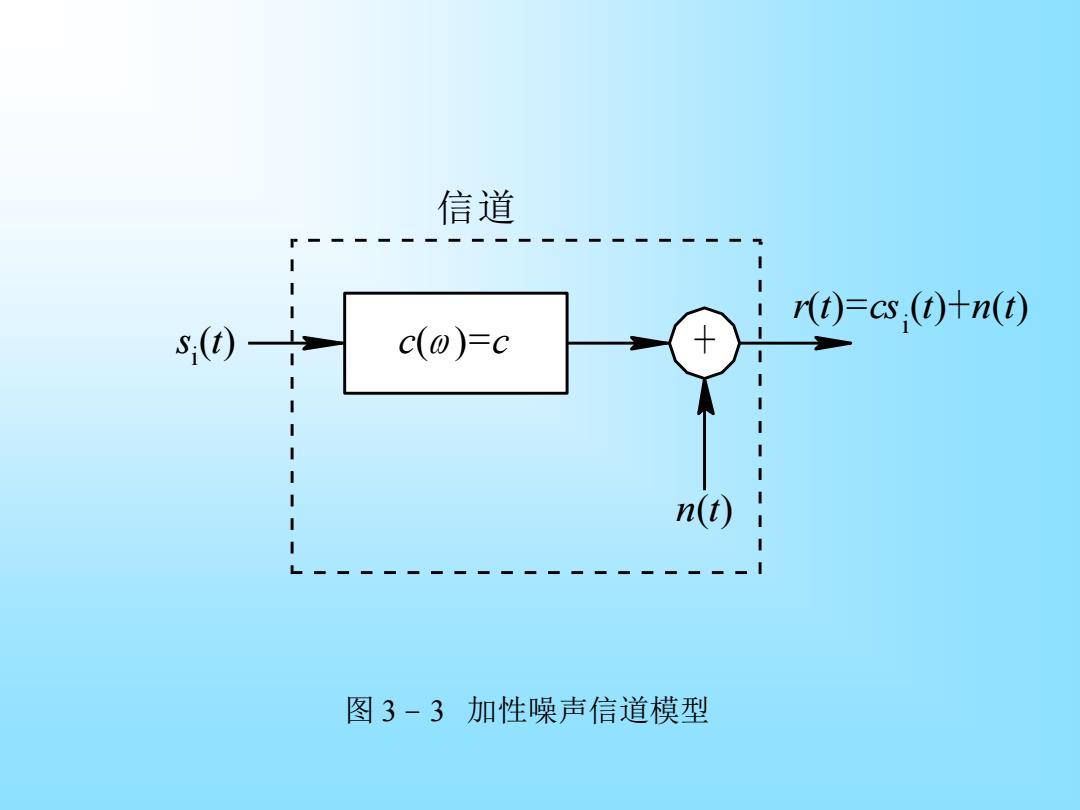
信道 (t)=cs,()十n(t) 5;(t) c(0)=c n(t) 图3-3加性噪声信道模型
图 3 – 3 加性噪声信道模型 c( )=c + r(t)=csi (t)+n(t) n(t) s i (t) 信 道

第二种形式C(O)在信号频带范围之内不是常数,但不随 时间变化,其模型如图3·4所示。这种信道在数学上可表示 为带有加性噪声的线性滤波器,若信道输入信号为$(),则信 道输出为 r(t)=s,(t)+n(t)=c(t)*s(t)+n(t) (3.1-5) 式中,*为卷积运算。 第三种形式C(o)在信号频带范围之内不是常数,且随时间 变化,其模型如图3-5所示。如电离层反射信道、移动通信 信道都具有这种特性。这种信道在数学上可表示为带有加性 噪声的线性时变滤波器。信道特性可以表征为时变单位冲激 响应c(t,),此时信道传输函数为C(o,)。若信道输入信号为 s(),则信道输出为
第二种形式C(ω)在信号频带范围之内不是常数,但不随 时间变化,其模型如图 3 - 4 所示。这种信道在数学上可表示 为带有加性噪声的线性滤波器,若信道输入信号为si (t),则信 r(t)=so (t)+n(t)=c(t)*si (t)+n(t) (3.1 - 5) 式中, *为卷积运算。 第三种形式C(ω)在信号频带范围之内不是常数,且随时间 变化, 其模型如图 3 - 5 所示。如电离层反射信道、移动通信 信道都具有这种特性。这种信道在数学上可表示为带有加性 噪声的线性时变滤波器。信道特性可以表征为时变单位冲激 响应c(t, τ), 此时信道传输函数为C(ω, τ)。若信道输入信号为 si (t),则信道输出为
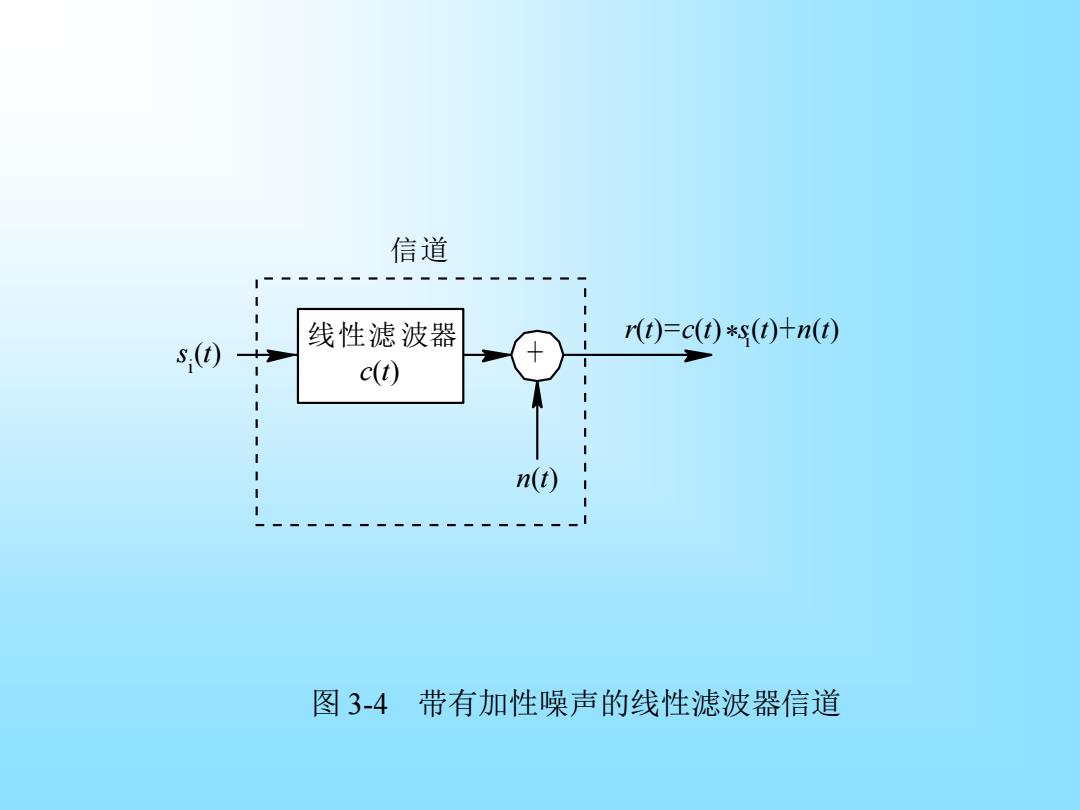
信道 (t)=c()*(t)十n(t) () 线性滤波器 c(t) n(t) 图3-4带有加性噪声的线性滤波器信道
图 3-4 带有加性噪声的线性滤波器信道 线性滤波器 c(t) + r(t)=c(t) si (t)+n(t) n(t) s i (t) 信 道 *