
仁 五 02 Z= Z12Z31 12+Z23+Z31 乙=乙+23+☑☑ Z3 Z2= Z12Z23 二→ Z23=Z2+Z3+ Z2·Z3 Z12+Z23+Z31 Z Z3= Z23·Z31 Z1=Z3+Z1+ 3·Z Z12+Z23+Z31 Z2
⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ + + ⋅ = + + ⋅ = + + ⋅ = 12 23 31 23 31 3 12 23 31 12 23 2 12 23 31 12 31 1 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ ⋅ = + + ⋅ = + + ⋅ = + + 2 3 1 31 3 1 1 2 3 23 2 3 3 1 2 12 1 2 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z
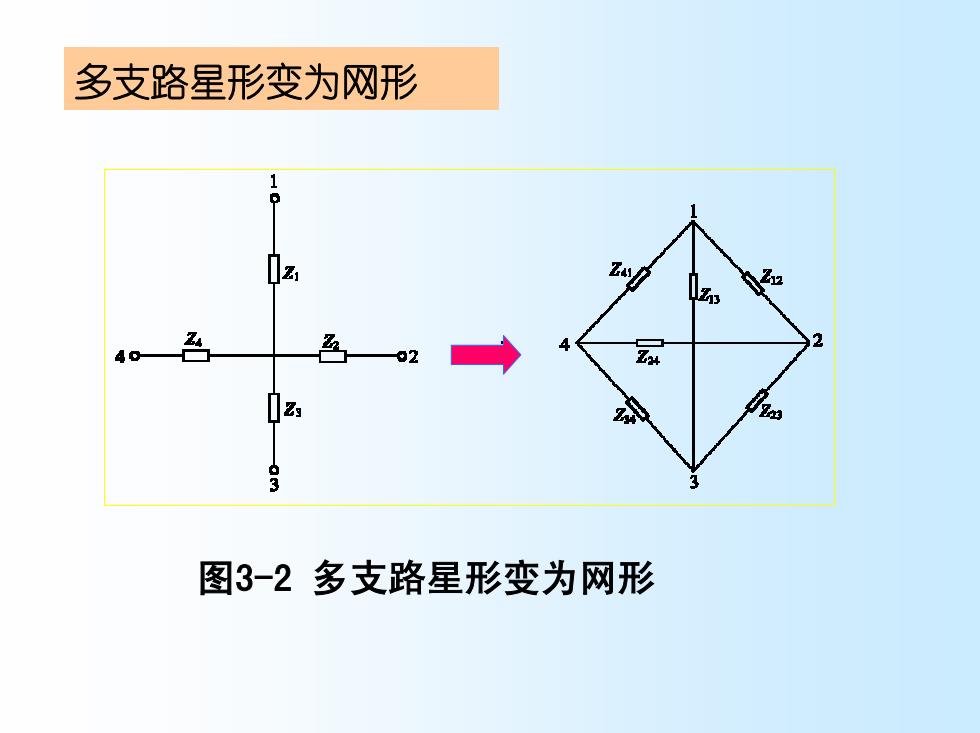
多支路星形变为网形 40 色 02 图3-2多支路星形变为网形
多支路星形变为网形 图3-2 多支路星形变为网形
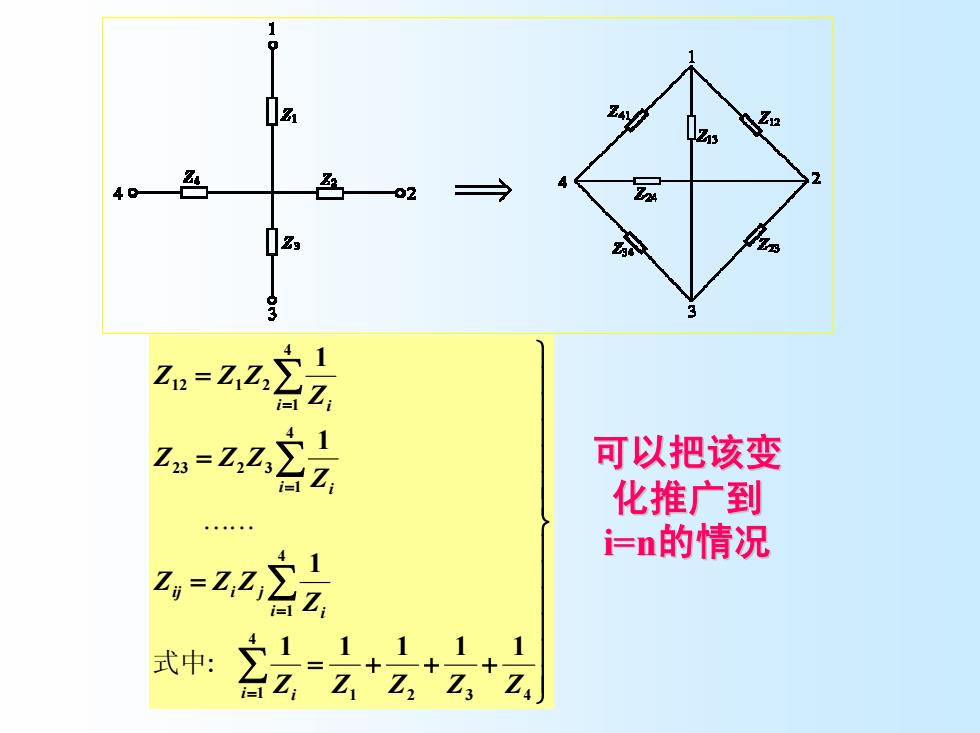
z 40 色 02 → lz, i=1 -2 可以把该变 化推广到 =n的情况 名-222法 式中:
⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ = + + + = = = ∑ ∑ ∑ ∑ = = = = 1 2 3 4 4 1 4 1 4 1 23 2 3 4 1 12 1 2 1 1 1 1 1 1 1 1 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i ij i j i i i i 式中: K K 可以把该变 化推广到 i=n的情况
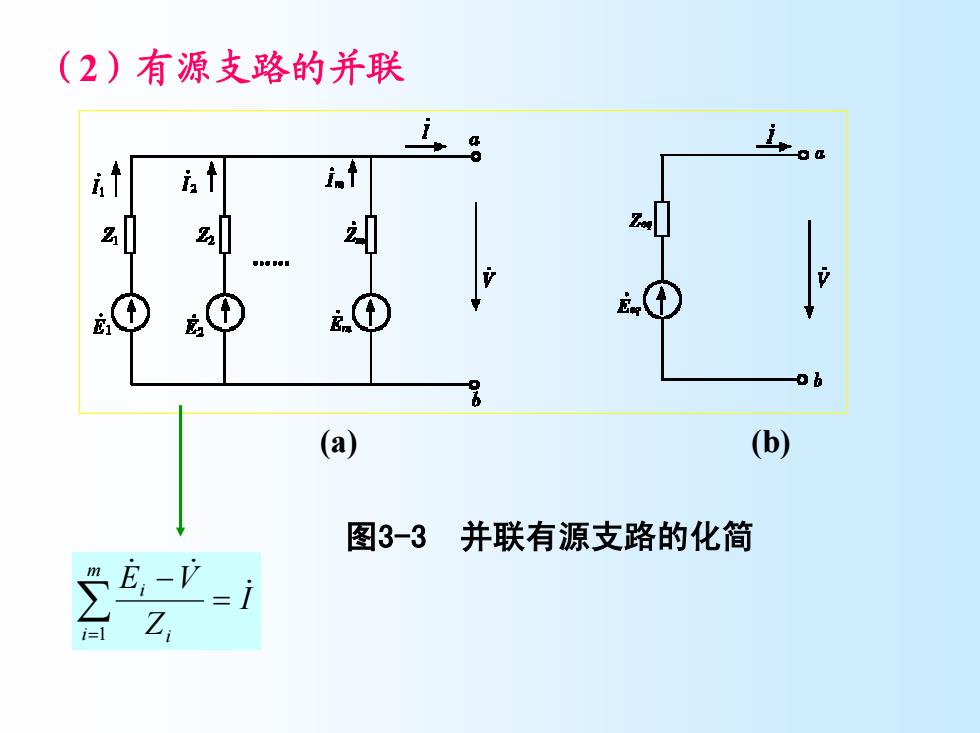
(2)有源支路的并联 it 的 (a) (b) 图3-3 并联有源支路的化简 Z
(2)有源支路的并联 图3-3 并联有源支路的化简 I Z E V m i i i & & & = − ∑ =1 (a) (b)
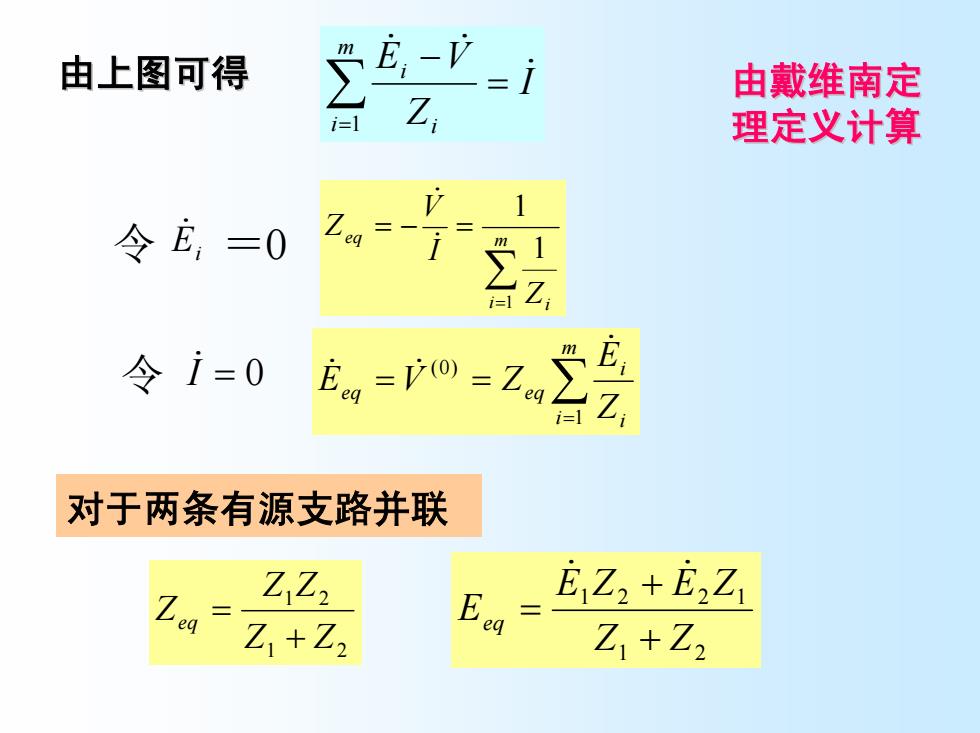
由上图可得 -=i 由戴维南定 Z 理定义计算 1 令龙,=0 令i=0 E=0=2 Z 对于两条有源支路并联 Z Z E Z2 +E2Z Z1+Z2 Z1+Z2
I Z E V m i i i & & & = − ∑ =1 由上图可得 由戴维南定 理定义计算 ∑ = = − = m i i eq Z I V Z 1 1 1 & & Ei 令 = & 0 ∑ = = = m i i i eq eq Z E E V Z 1 (0) & 令 I& = 0 & & 对于两条有源支路并联 1 2 1 2 2 1 Z Z E Z E Z Eeq ++ = & & 1 2 1 2 Z Z Z Z Zeq + =