
定义:描述随机事件A发生可能性大小的数值,称为A的概率 记作P(A),简记为P。假如临床观察中治疗200病人的样本,求得 治愈率为75%,这只是一个频率。实际应用中,当概率不易求得时, 常用n→∞时的频率作为概率的估计值。但当n较少时,频率的波动 性是很大的,用于估计概率是不可靠的。 随机事件概率的大小在0与1之间。 P值越接近1,表示某事件发生的可能性越大: P值越接近0,表示某事件发生的可能性越小。 严格说,P=1表示事件必然发生,P0表示事件不可能发生,他 们是确定性的,不是随机事件,但可把他们看成随机事件的特例。 统计分析中的很多结论都是带有概率性的。习惯上将P≤0.05 称为小概率事件,表示在一次实验或观察中该事件发生的可能性很 小,可以视为很可能不发生。 《医学统计学》的学习重点是: 1、掌握其基本知识、基本技能、基本概念、基本方法。 建立逻辑思维方法和提高分析问题的能力。 2、掌握调查设计和试验设计的基本原则。 培养收集、整理、分析统计资料的系统工作能力。 3、掌握一套统计软件的使用方法(SAS、SPSS、STATA等)。 能够达到在完成《医学统计学》课程后,独立完成科研论 文和正确应用统计方法
定义:描述随机事件 A 发生可能性大小的数值,称为 A 的概率, 记作 P(A),简记为 P。假如临床观察中治疗 200 病人的样本,求得 治愈率为 75%,这只是一个频率。实际应用中,当概率不易求得时, 常用 n→∞时的频率作为概率的估计值。但当 n 较少时,频率的波动 性是很大的,用于估计概率是不可靠的。 随机事件概率的大小在 0 与 1 之间。 P 值越接近 1,表示某事件发生的可能性越大; P 值越接近 0,表示某事件发生的可能性越小。 严格说,P=1 表示事件必然发生,P=0 表示事件不可能发生,他 们是确定性的,不是随机事件,但可把他们看成随机事件的特例。 统计分析中的很多结论都是带有概率性的。习惯上将 P≤0.05 称为小概率事件,表示在一次实验或观察中该事件发生的可能性很 小,可以视为很可能不发生。 《医学统计学》的学习重点是: 1、掌握其基本知识、基本技能、基本概念、基本方法。 建立逻辑思维方法和提高分析问题的能力。 2、掌握调查设计和试验设计的基本原则。 培养收集、整理、分析统计资料的系统工作能力。 3、掌握一套统计软件的使用方法(SAS、SPSS、STATA 等)。 能够达到在完成《医学统计学》课程后,独立完成科研论 文和正确应用统计方法

第二讲集中趋势 举例 设有A、B两名新战士,他们的射击技术可用下面的分布来表示: 战十 击中环数8 010 击中环数8 10 对应概率0.30.10.6 问哪一个战士射击技术较好?1、频数分布表 1人频数表的编制 相同观察结果出现的次数称为频数。将所有观察结果的频数按一定顺序排列 在 起便是频数表(frequency table)。 步骤: ①找出最大和最小值,计算极差R=Xmr一Xm ②根据斯梯阶公式确定组距 H= 1+3.3221ogn ③扫描样本值,划记后获得频数 2人、频数表的用途 ①大样本数据(不限于计量资料)常用的表达方式, ②便于观察数据的分布类型。 ③便于发现资料中远离群体的某些特大或特小的可疑值,必要时经 检验后舍去
第二讲 集中趋势 举例 设有 A、B 两名新战士,他们的射击技术可用下面的分布来表示: 战 士 A 战 士 B 击中环数 8 9 10 击中环数 8 9 10 对应概率 0.3 0.1 0.6 对应概率 0.2 0.5 0.3 问哪一个战士射击技术较好?1、频数分布表 1)、频数表的编制 相同观察结果出现的次数称为频数。将所有观察结果的频数按一定顺序排列 在一起便是频数表(frequency table)。 步骤: ① 找出最大和最小值,计算极差 R=Xmax―Xmin ② 根据斯梯阶公式确定组距 n R H 1+ 3.322log = ③ 扫描样本值,划记后获得频数 2)、频数表的用途 ① 大样本数据(不限于计量资料)常用的表达方式。 ② 便于观察数据的分布类型。 ③ 便于发现资料中远离群体的某些特大或特小的可疑值,必要时经 检验后舍去
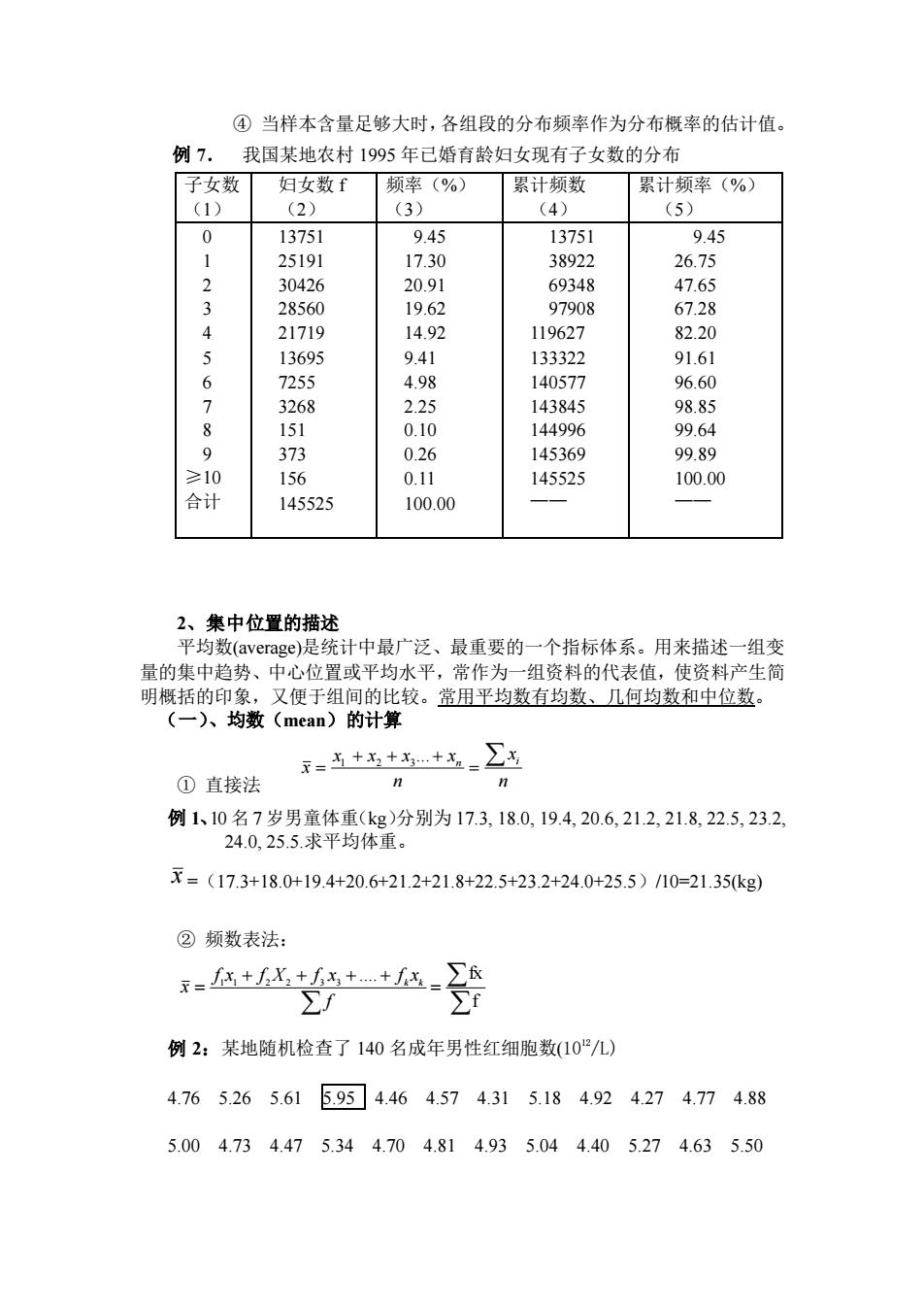
④当样本含量足够大时,各组段的分布频率作为分布概率的估计值。 例7.我国某地农村1995年已婚育龄妇女现有子女数的分布 子女数 妇女数f 频率(%) 累计频数 累计频率(%) (1) (2) (3) (4) (5) 0 13751 945 13751 945 2519 17.30 38922 2615 3042( 20.9 6934 47.65 3 28560 19.62 97908 67.28 4 21719 1492 119627 82.20 13695 9.41 133322 91.61 6 140577 14384 8 1话10 144996 99.64 9 373 26 145369 99.89 ≥10 156 011 145525 100.00 合计 145525 100.00 2、集中位置的描述 平均数(a ae)是统计中最广泛、最重要的一个指标体系。用来描述一组变 量的集中趋势、中心位置或平均水平,常作为 组资料的代表值 使资 料产生简 明概括的印象,又便于组间的比较。常用平均数有均数、几何均数和中位数。 (一)、均数(mean)的计算 =名+++_∑ ①直接法 例1、10名7岁男童体重(kg)分别为17.3,18.0,19.4,20.6,212,21.8,22.5,23.2 24.0.25.5.求平均体重。 x=(17.3+18.0+19.4+20.6+21.2+21.8+22.5+23.2+24.0+25.5)10=21.35kg) ②频数表法 =压+X,+++区_∑& ∑f 例2:某地随机检查了140名成年男性红细胞数(10/L) 4.765.265.615.95☐4.464.574.315.184.924.274.774.88 5.004.734.475.344.704.814.935.044.405.274.635.50
④ 当样本含量足够大时,各组段的分布频率作为分布概率的估计值。 例 7. 我国某地农村 1995 年已婚育龄妇女现有子女数的分布 子女数 (1) 妇女数 f (2) 频率(%) (3) 累计频数 (4) 累计频率(%) (5) 0 1 2 3 4 5 6 7 8 9 ≥10 合计 13751 25191 30426 28560 21719 13695 7255 3268 151 373 156 145525 9.45 17.30 20.91 19.62 14.92 9.41 4.98 2.25 0.10 0.26 0.11 100.00 0. 13751 38922 69348 97908 119627 133322 140577 143845 144996 145369 145525 —— 9.45 26.75 47.65 67.28 82.20 91.61 96.60 98.85 99.64 99.89 100.00 —— 2、集中位置的描述 平均数(average)是统计中最广泛、最重要的一个指标体系。用来描述一组变 量的集中趋势、中心位置或平均水平,常作为一组资料的代表值,使资料产生简 明概括的印象,又便于组间的比较。常用平均数有均数、几何均数和中位数。 (一)、均数(mean)的计算 ① 直接法 n x n x x x x x n i = + + + = ... 1 2 3 例 1、10 名 7 岁男童体重(kg)分别为 17.3, 18.0, 19.4, 20.6, 21.2, 21.8, 22.5, 23.2, 24.0, 25.5.求平均体重。 x =(17.3+18.0+19.4+20.6+21.2+21.8+22.5+23.2+24.0+25.5)/10=21.35(kg) ② 频数表法: f .... fx 1 1 2 2 3 3 = + + + + = f f x f X f x f x x k k 例 2:某地随机检查了 140 名成年男性红细胞数(1012/L) 4.76 5.26 5.61 5.95 4.46 4.57 4.31 5.18 4.92 4.27 4.77 4.88 5.00 4.73 4.47 5.34 4.70 4.81 4.93 5.04 4.40 5.27 4.63 5.50
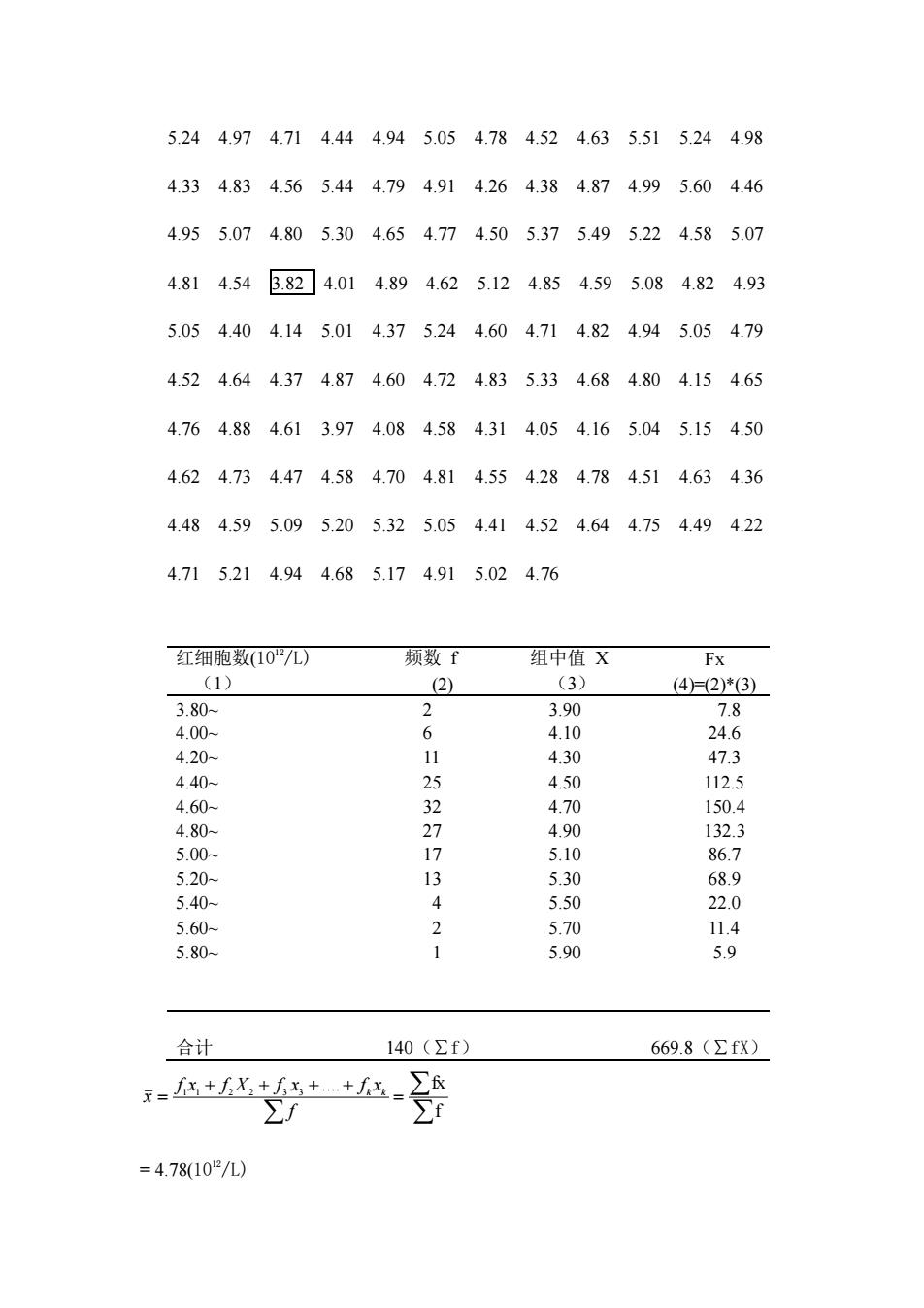
5.244.974.714.444.945.054.784.524.635.515.244.98 4.334.834.565.444.794.914.264.384.874.995.604.46 4.955.074.805.304.654.774.505.375.495.224.585.07 4.814.543.824.014.894.625.124.854.595.084.824.93 5.054.404.145.014.375.244.604.714.824.945.054.79 4.524.644.374.874.604.724.835.334.684.804.154.65 4.764.884.613.974.084.584.314.054.165.045.154.50 4.624.734.474.584.704.814.554.284.784.514.634.36 4.484.595.095.205.325.054.414.524.644.754.494.22 4.715.214.944.685.174.915.024.76 红细胞数(10九) 频数f 组中值X (1) (3) (4=(2)3) 3.80- 2 3.90 7.8 4.00- 6 4.10 24.6 4.20 11 4.30 47.3 252 4.80 4.90 132.3 5.00 17 5.10 86.7 5.20 6 5.30 68.9 5.40 4 5.50 220 560- 2 570 114 5.80 1 5.90 5.9 合计 140(∑f) 669.8(∑fX) x=压+fX,+++f区 E& ∑f ∑f =4.7810/L)
5.24 4.97 4.71 4.44 4.94 5.05 4.78 4.52 4.63 5.51 5.24 4.98 4.33 4.83 4.56 5.44 4.79 4.91 4.26 4.38 4.87 4.99 5.60 4.46 4.95 5.07 4.80 5.30 4.65 4.77 4.50 5.37 5.49 5.22 4.58 5.07 4.81 4.54 3.82 4.01 4.89 4.62 5.12 4.85 4.59 5.08 4.82 4.93 5.05 4.40 4.14 5.01 4.37 5.24 4.60 4.71 4.82 4.94 5.05 4.79 4.52 4.64 4.37 4.87 4.60 4.72 4.83 5.33 4.68 4.80 4.15 4.65 4.76 4.88 4.61 3.97 4.08 4.58 4.31 4.05 4.16 5.04 5.15 4.50 4.62 4.73 4.47 4.58 4.70 4.81 4.55 4.28 4.78 4.51 4.63 4.36 4.48 4.59 5.09 5.20 5.32 5.05 4.41 4.52 4.64 4.75 4.49 4.22 4.71 5.21 4.94 4.68 5.17 4.91 5.02 4.76 红细胞数(1012/L) (1) 频数 f (2) 组中值 X (3) Fx (4)=(2)*(3) 3.80~ 4.00~ 4.20~ 4.40~ 4.60~ 4.80~ 5.00~ 5.20~ 5.40~ 5.60~ 5.80~ 2 6 11 25 32 27 17 13 4 2 1 3.90 4.10 4.30 4.50 4.70 4.90 5.10 5.30 5.50 5.70 5.90 7.8 24.6 47.3 112.5 150.4 132.3 86.7 68.9 22.0 11.4 5.9 合计 140(∑f) 669.8(∑fX) f .... fx 1 1 2 2 3 3 = + + + + = f f x f X f x f x x k k = 4.78(1012/L)

均数的两个重要特征 各离均差的总和等于零 ∑x-网=0 证明:∑(x,-x)=∑x,-nx=∑x,-∑x=0 ②各离均差的平方和小于各观察值X与任何数a之差的平方 ∑x-x<∑x-a 均数的应用: 1.用来描述一组变量值的平均水平,具有代表性,因此变量值必须是同质的。 2.适用于呈正态分布(对称分布)的资料。 (2)几何均数(geometric mean).的计算 1)直接法 G=xx…x G=g图x+超名+8五)=电∑g马 例3:5人的血清滴度为:1:2,1:4,1:8,1:16,1:32,求平均滴度。 G=V2×4×8x16x32 LgG=(lg2+lg4+lg8+lg16+lg32)/5=0.903 G=g10.903=8 故平均滴度为1:8。 2)频数表法 例4:40名麻疹疫苗接种麻疹疫苗后一个月,血凝抑制抗体滴度见下表, 求平均滴度。 抗体滴度人数f滴度倒数X Lgx flgx☐
均数的两个重要特征: ① 各离均差的总和等于零 (x - x) = 0 证明: − = − = − = − − (xi x) xi n x xi xi 0 ② 各离均差的平方和小于各观察值 X 与任何数 a 之差的平方 2 2 (x - x) (x - a) 均数的应用: 1. 用来描述一组变量值的平均水平,具有代表性,因此变量值必须是同质的。 2. 适用于呈正态分布(对称分布)的资料。 (2)几何均数(geometric mean)的计算 1) 直接法 ) lg ) lg ( lg lg lg lg ( 1 1 2 1 1 2 3 n x n x x x G G x x x x n n n = − + + = − = 例 3:5 人的血清滴度为:1:2,1:4,1:8,1:16,1:32,求平均滴度。 n G = 2 481632 LgG=(lg2+lg4+lg8+lg16+lg32)/5=0.903 G=lg-10.903=8 故平均滴度为 1:8。 2) 频数表法 ) lg lg ( 1 = − f f x G 例 4:40 名麻疹疫苗接种麻疹疫苗后一个月,血凝抑制抗体滴度见下表, 求平均滴度。 抗体滴度 人数 f 滴度倒数 X LgX f*lgX