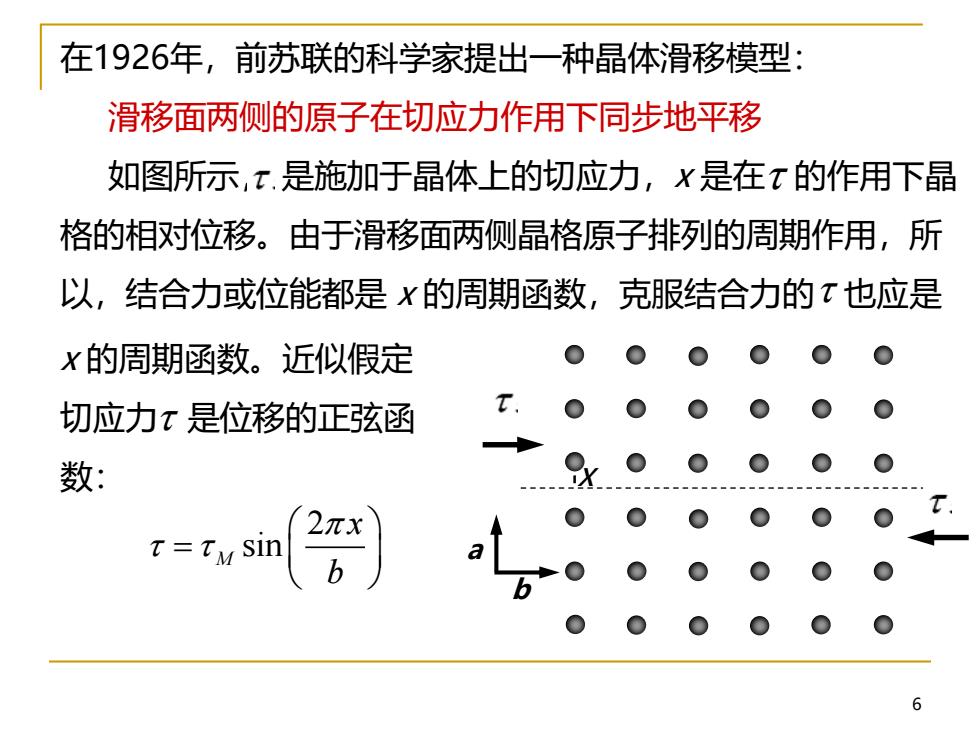
在1926年,前苏联的科学家提出一种晶体滑移模型: 滑移面两侧的原子在切应力作用下同步地平移 如图所示,x.是施加于晶体上的切应力,X是在T的作用下晶 格的相对位移。由于滑移面两侧晶格原子排列的周期作用,所 以,结合力或位能都是X的周期函数,克服结合力的τ也应是 x的周期函数。近似假定 切应力τ是位移的正弦函 数: b 6
6 在1926年,前苏联的科学家提出一种晶体滑移模型: 滑移面两侧的原子在切应力作用下同步地平移 如图所示, 是施加于晶体上的切应力,x 是在 的作用下晶 格的相对位移。由于滑移面两侧晶格原子排列的周期作用,所 以,结合力或位能都是 x 的周期函数,克服结合力的 也应是 2 sin M x b = b a x 的周期函数。近似假定 切应力 是位移的正弦函 数: x
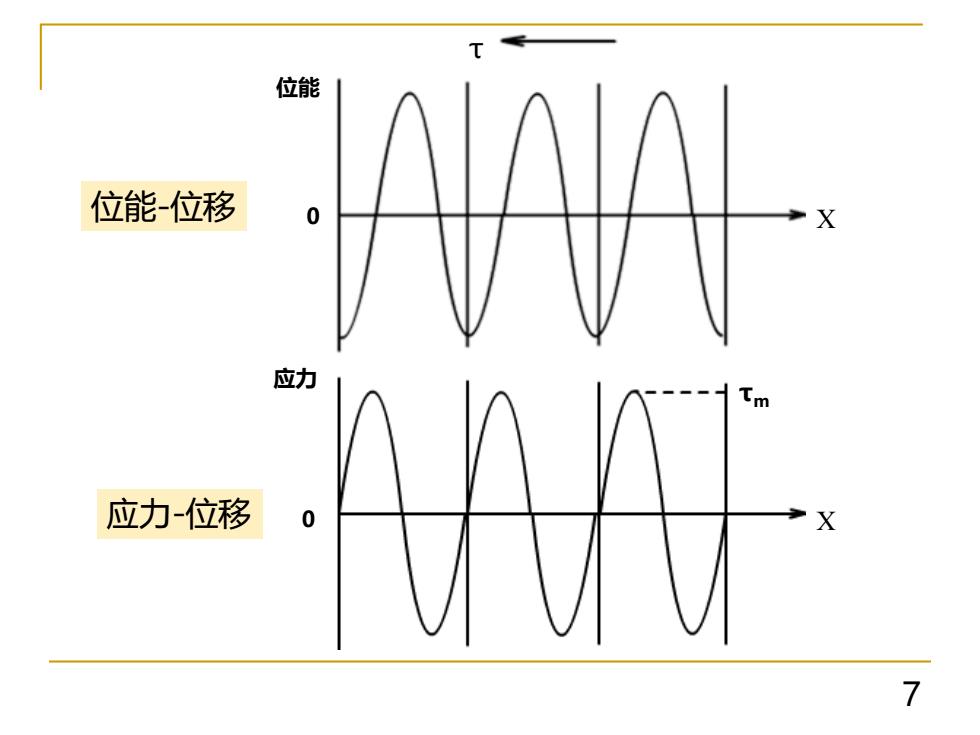
位能 位能位移 应力 应力位移
7 位能-位移 应力-位移 X X 位能 应力 0 0 τm τ

当x很小时,有sinx=x则: 2X b 式中TM应为最大应力, 即屈服强度。 由虎克定律=G) G为切变模量a为两层原子面间距。 tw= (b≤a 实验值与理论值相差 若a=b,此即为估算最大切应力(屈服 了3-4的数量级, why? G 2π 对一般金属材料G=10°~10Pa则t=109~1010Pa 但是,实验测量得:tw=l0Pa 8
8 x G a = ( ) 2 M G b b a a = 2 M G = 由虎克定律 G 为切变模量 a 为两层原子面间距。 2 M x b = 式中 应为最大应力,即屈服强度。 当 x 很小时,有sin x = x 则: 若a = b,此即为估算最大切应力(屈服强度)的理论公式。 但是,实验测量得: 10 Pa 6 M = 家胡克发现的,所以叫做胡克定律,又译为虎克定律。 M 10 ~ 10 Pa 10 11 对一般金属材料 G = 则 10 ~10 Pa 9 10 M = 实验值与理论值相差 了3-4的数量级, why?

1934年Taylor G.T.等人提出了新的模型: 0000.0000000000000000 0000000 。0.00.0 。000。0 0000000 0000000 0.00000 000000G4-0.6-。000g00e0000e-6e。e9 00000000000000 00000000000000 00.00。0000000 1、滑移首先在滑移面附近很小区域内发生,在滑移区与未滑移区的 交界处,有一部分的粒子偏离原来点阵的位置排列(更密或更疏),把这 种晶体缺陷称作位错(或位错线)。 2、在应力作用下,通过位错处原子进一步滑移,使位错线逐渐向前移 动,最后,完成滑移一个原子间距。 由于原子的滑移只在位错线附近进行,所需应力比上下 层之间同时滑动要小的多
9 b a t x t 1934年Taylor G .T.等人提出了新的模型: 1、滑移首先在滑移面附近很小区域内发生,在滑移区与未滑移区的 交界处,有一部分的粒子偏离原来点阵的位置排列(更密或更疏),把这 种晶体缺陷称作位错(或位错线)。 2、在应力作用下,通过位错处原子进一步滑移,使位错线逐渐向前移 动,最后,完成滑移一个原子间距。 由于原子的滑移只在位错线附近进行,所需应力比上下 层之间同时滑动要小的多

1934年Taylor G.T.等人提出了新的模型: 1、滑移首先在滑移面附近很小区域内发生,在滑移区与未滑移区的 交界处,有一部分的粒子偏离原来点阵的位置排列(更密或更疏),把这 种晶体缺陷称作位错(或位错线)。 2、在应力作用下,通过位错处原子进一步滑移,使位错线逐渐向前移 动,最后,完成滑移一个原子间距。 由于原子的滑移只在位错线附近进行,所需应力比上下 层之间同时滑动要小的多
10 1934年Taylor G .T.等人提出了新的模型: 1、滑移首先在滑移面附近很小区域内发生,在滑移区与未滑移区的 交界处,有一部分的粒子偏离原来点阵的位置排列(更密或更疏),把这 种晶体缺陷称作位错(或位错线)。 2、在应力作用下,通过位错处原子进一步滑移,使位错线逐渐向前移 动,最后,完成滑移一个原子间距。 由于原子的滑移只在位错线附近进行,所需应力比上下 层之间同时滑动要小的多