
aKμ=1+=今称为动荷因数,则gOa = KaOstGK,PlMdmax=K,M梁的弯矩:S4MK.PldmaxOdmax梁的最大动应力:W4W
令 称为动荷因数,则 g a Kd =1+ d = Kd st 梁的弯矩: 4 max K Pl M K M d d = d st = 梁的最大动应力: W K Pl W Md d d 4 max max = =

例12-2长度l=12m的16号工字钢,用横截面面积为A-108mm2的钢索起吊,如图a所示,并以等加速度a=10m/s2上升。若只考虑工字钢的重量而不计吊索自重,试求吊索的动应力,以及工字钢在危险点的动应力od,max2ml 4ml4m12mCBA(a)2.484m7.032m12.484m(d)BA
例12-2 长度 l=12m 的16号工字钢,用横截面面积 为 A=108mm2 的钢索起吊,如图a所示,并以等加速 度 a=10m/s2 上升。若只考虑工字钢的重量而不计吊 索自重,试求吊索的动应力,以及工字钢在危险点的 动应力d,max (d) A B 2.484m 7.032m 2.484m A a 4m B 2m 2m C y z 4m (a)

解:将集度为J=Apa的惯性力加在工字钢上,使工字钢上的起吊力与其重量和惯性力假想地组成平衡力系。若工字钢单位长度的重量记为st,则惯性力集度为9=9st ×g于是,工字钢上总的均布力集度为q= Qst + qa = qst(1+ ~)gK=1+α则q=Kaqst引入动荷因数g
于是,工字钢上总的均布力集度为 (1 ) st d st g a q = q + q = q + g a qd = qst 解:将集度为 qd=Aa 的惯性力加在工字钢上,使工 字钢上的起吊力与其重量和惯性力假想地组成平衡力 系。若工字钢单位长度的重量记为 qst ,则惯性力集 度为 引入动荷因数 g a Kd =1+ 则 q = Kd qst
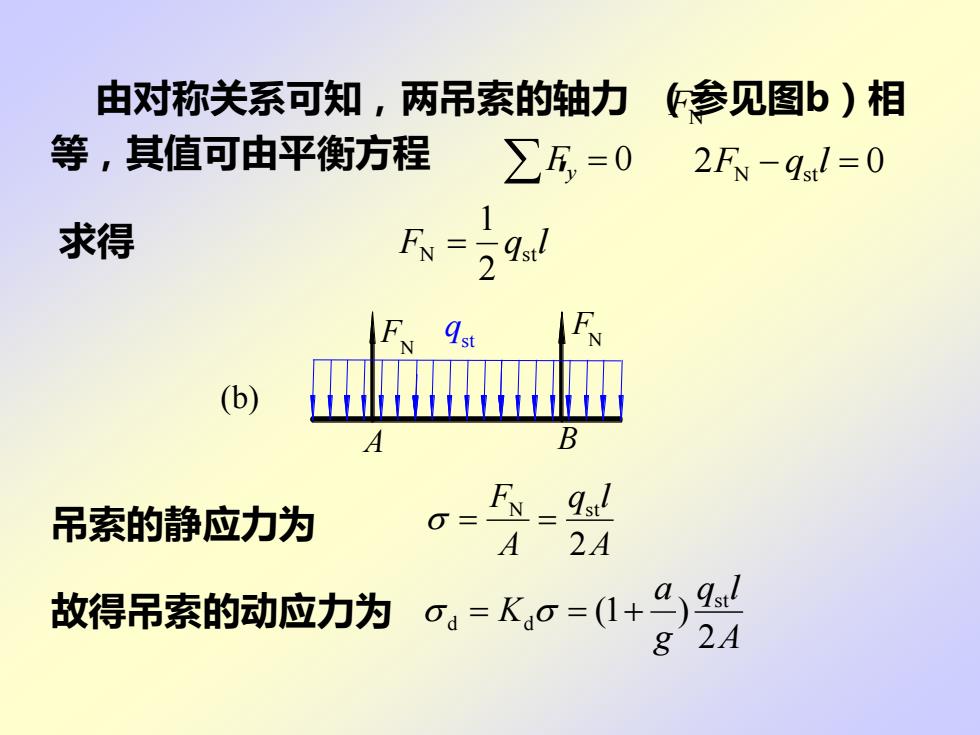
由对称关系可知,两吊索的轴力(参见图b)相等,其值可由平衡方程ZF,=02F-qstl =0求得Fn=qstl2FFNq(b)BAFn - qstl=吊索的静应力为2AA为 =Kg=(1+)故得吊索的动应力为g 2A
由对称关系可知,两吊索的轴力 (参见图b)相 等,其值可由平衡方程 , FN Fy = 0 2FN − qstl = 0 求得 F q l N st 2 1 = 吊索的静应力为 A q l A F 2 N st = = 故得吊索的动应力为 A q l g a K 2 (1 ) st d = d = + (b) A B FN N q F st

由型钢表查得st=20.5kg/m=(20.5N/m)g及已知数据代入上式,即得10m/s 2(20.5 ×9.81N/m)(12m)2=22.6MPa0 =(1+9.81m/s2×108×10-6同理,工字钢危险截面上危险点处的动应力M.Odmx = KgOmx =(1+ ~)maxW.g
由型钢表查得 qst=20.5kg/m=(20.5N/m)g及已知数据 代入上式,即得 22.6MPa 2 108 10 (20.5 9.81N/m)(12m) ) 9.81m/s 10m/s (1 2 6 2 d = = + − 同理,工字钢危险截面上危险点处的动应力 Wz M g a K max d ,max d max = = (1+ )