【例2-5-3】 试用齐性定理计算图所示梯形电路中的电流, 解采用”倒推法”。 6Ω 2Ω 设 i1=1A 则 uab'=(2×1+4×1)V=6V 120V 3 =(5+1)A=3A l ' (6×3+6)V=24V 根据齐性定理,有 4= i “倒推法”:由远及近,先设 i=4=120 11=1A 故 ×3A=15A 24
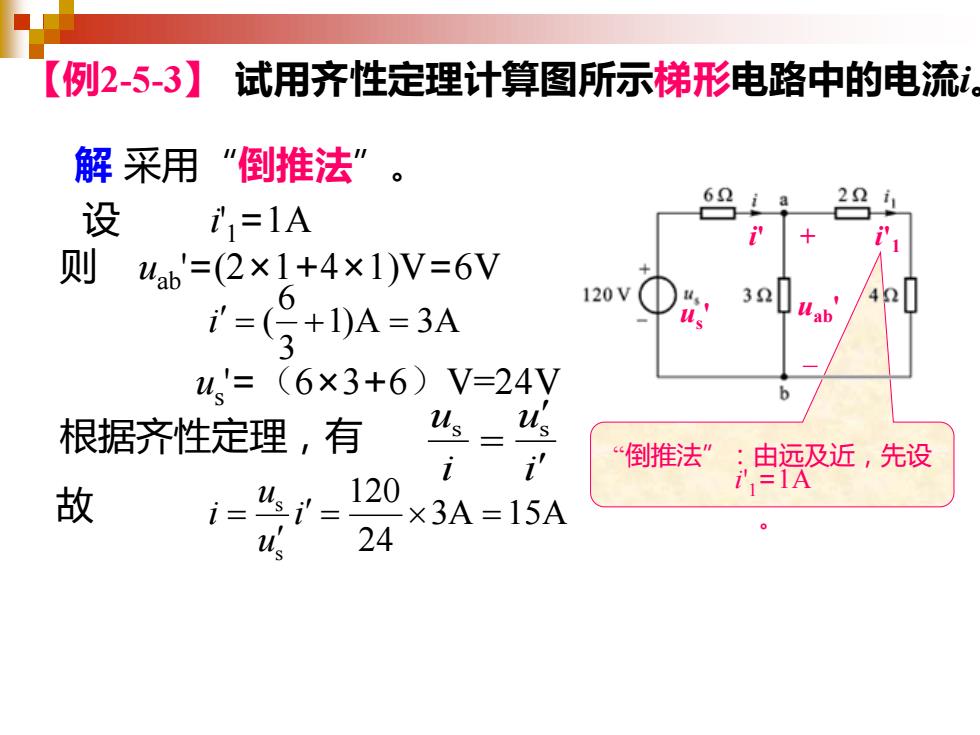
【例2-5-3】 试用齐性定理计算图所示梯形电路中的电流i。 解 采用“倒推法” 。 设 i' 1=1A 则 uab '=(2×1+4×1)V=6V 1)A 3A 3 6 i = ( + = us '=(6×3+6)V=24V 根据齐性定理,有 i u i u = s s 3A 15A 24 120 s s = = = i u u i i' 1 i' uab ' + _ us ' 故 “倒推法”:由远及近,先设 i' 1=1A
【例4-4】图示方框No内部(黑箱中)为不含有独立电 源的线性电路,内部结构不详,若已知:当Uς=1V, Ls=1A时,响应U2=0V;当Us=10V,Is=0A时,响应 U2=1V;求当Us=0V,Is=10A时,响应U2的值。 U2=KUs+K2Is No
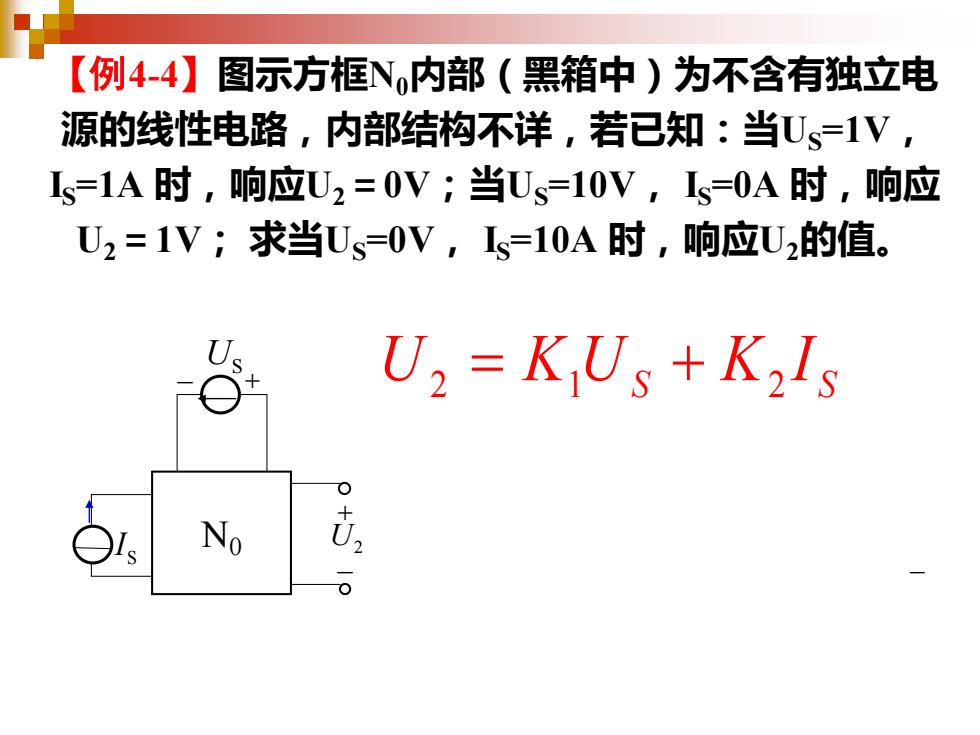
【例4-4】图示方框N0内部(黑箱中)为不含有独立电 源的线性电路,内部结构不详,若已知:当US=1V, IS=1A 时,响应U2=0V;当US=10V, IS=0A 时,响应 U2=1V; 求当US=0V, IS=10A 时,响应U2的值。 N0 S I US + − U2 − + − U K U K I 2 1 2 = +S S
§2-6置换定理 一、置换(替代)定理 若电路中任一支路的电压4或电流,已知,且该支 路与电路中的其他支路无耦合,那么这一条支路可 以用一电压等于4的电压源置换,或用一个电流等于 的电流源置换,也可以用阻值为w/的电阻置换, 置换后电路中各支路电压和电流保持不变。 被置换的支路或 二端网络
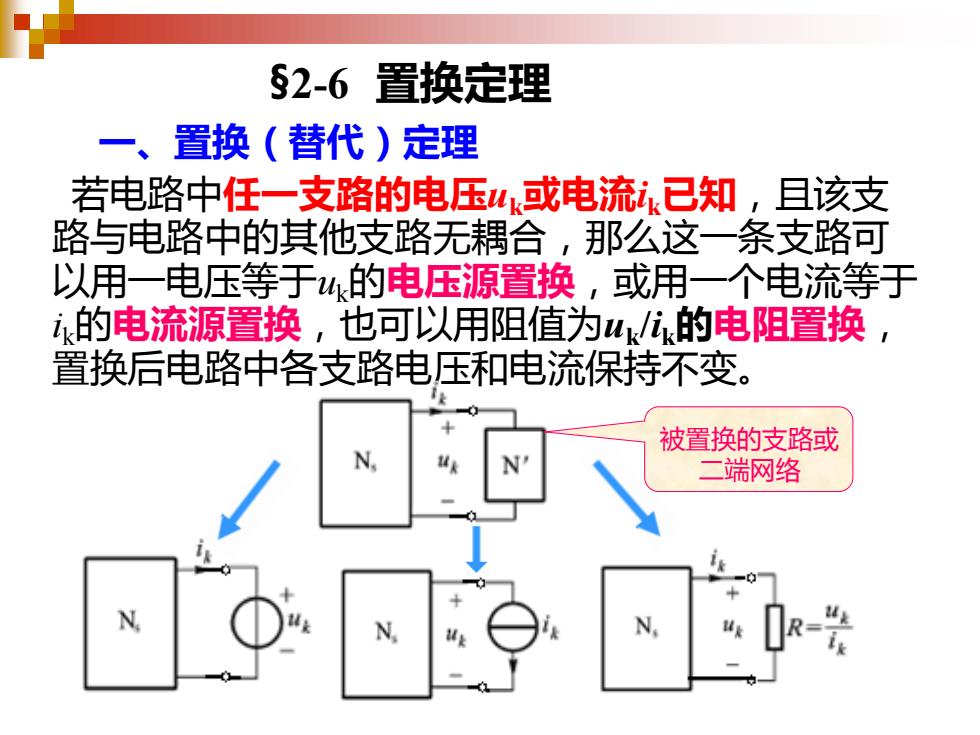
§2-6 置换定理 若电路中任一支路的电压uk或电流ik已知,且该支 路与电路中的其他支路无耦合,那么这一条支路可 以用一电压等于uk的电压源置换,或用一个电流等于 ik的电流源置换,也可以用阻值为uk /ik的电阻置换, 置换后电路中各支路电压和电流保持不变。 一、置换(替代)定理 被置换的支路或 二端网络
【例2-6-1】已知图(a)所示电路中15电阻的电流为1=1.2A 10Ω电阻的电压为U1=2V。试用置换定理重新计算U1。 L1102 12501 20V 152电阻用 1.2A的电流源 (a) 置换 (b) 解将15Ω电阻用1.2A的电流源置换得图(b)所示 电路。根据KCL列节点1方程,得 I1=1.2-1=0.2A 用电阻元件的VAR,得 U1=10×0.2=2V
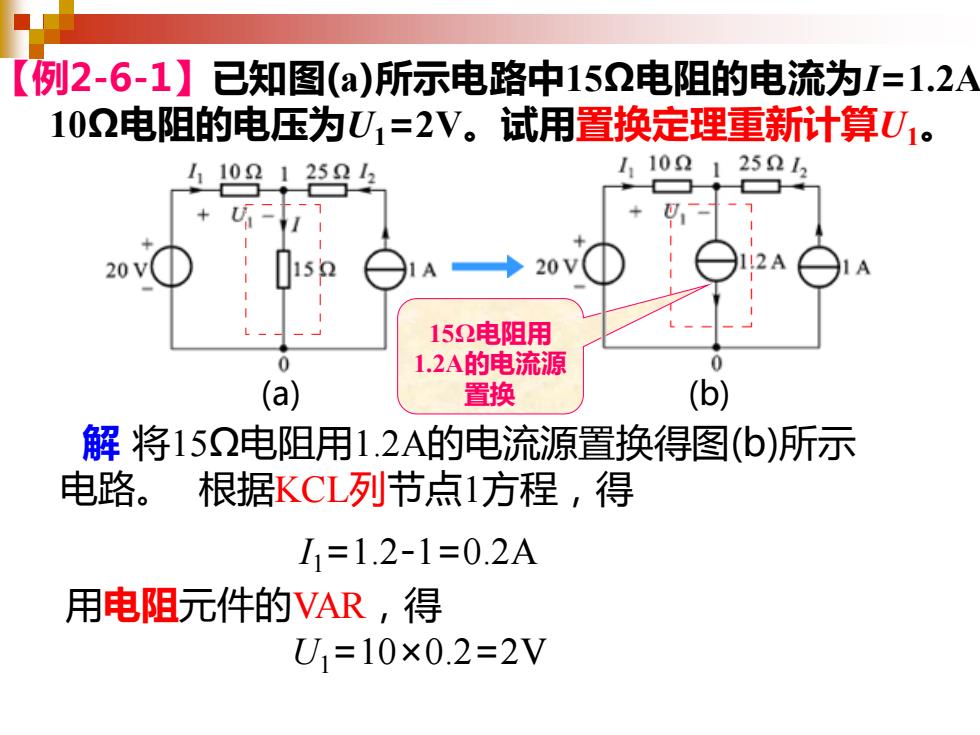
(a) 用电阻元件的VAR,得 U1=10×0.2=2V (b) 解 将15Ω电阻用1.2A的电流源置换得图(b)所示 电路。 I1=1.2-1=0.2A 【例2-6-1】已知图(a)所示电路中15Ω电阻的电流为I=1.2A, 10Ω电阻的电压为U1=2V。试用置换定理重新计算U1。 15Ω电阻用 1.2A的电流源 置换 根据KCL列节点1方程,得

§2-7 戴维宁定理和诺顿定理 戴维宁定理 1、内容 任何一个含独立电源、线性电阻和受控源 的二端网络,对外电路来说,可以用一个电 压源和电阻的串联组合等效置换,此电压源 的电压等于二端网络的开路电压,电阻等于 二端网络的全部独立电源置零后的等效电阻
戴维宁定理 1、内容 任何一个含独立电源、线性电阻和受控源 的二端网络,对外电路来说,可以用一个电 压源和电阻的串联组合等效置换,此电压源 的电压等于二端网络的开路电压,电阻等于 二端网络的全部独立电源置零后的等效电阻 。 §2-7 戴维宁定理和诺顿定理