《电路》课程教学课件（电路原理）第2章 电路的基本分析方法（3/3）

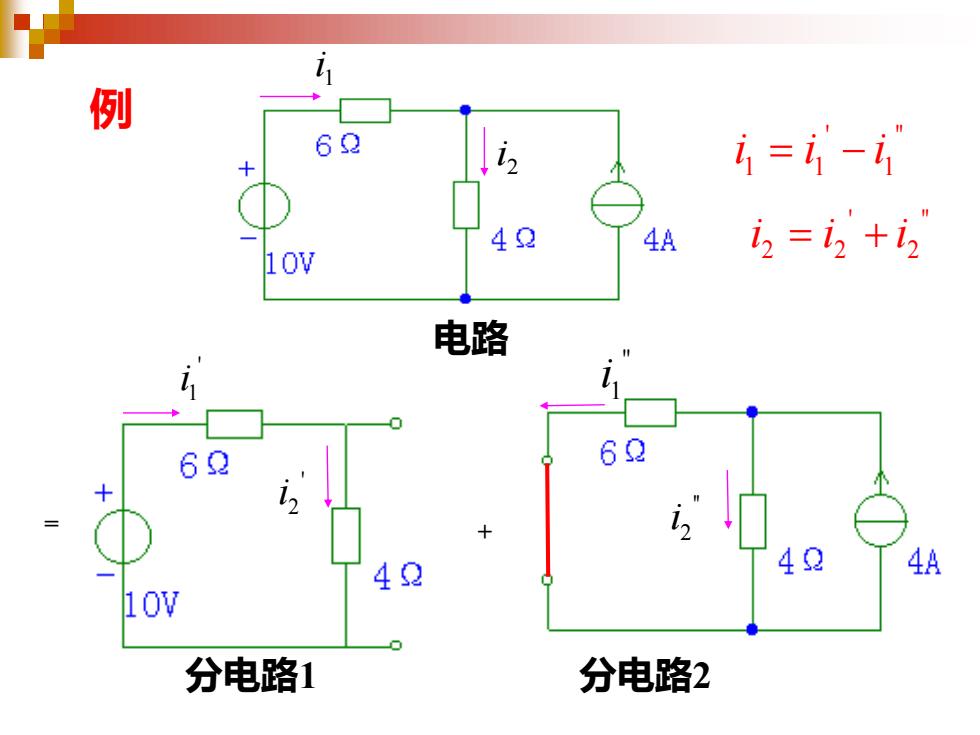
例 62 1=1- 42 4A i2=2+2 10V 电路 62 62 42 4A 10V 分电路1 分电路2

= + 1 i 2 i ' 1 i ' 2 i '' 1 i '' 2 i 例 ' '' 2 2 2 i i i = + ' '' 111 iii = − 分电路1 分电路2 电路

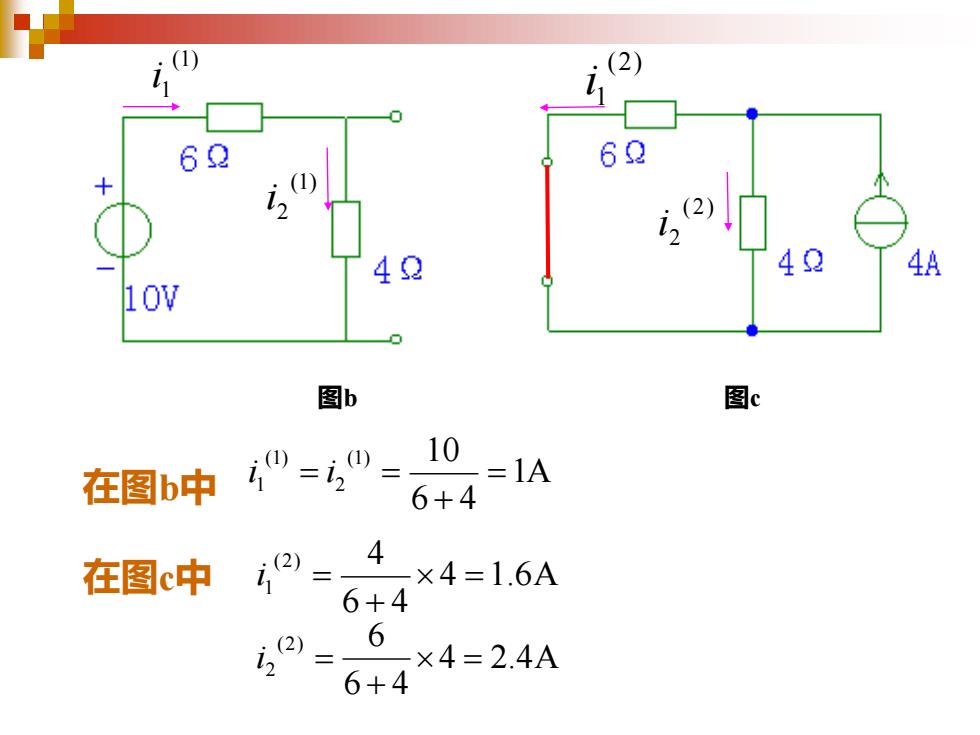
6 62 4A 10V 图b 图c 在图b中 ”="=10 =1A 6+4 在图c中 2= 4 ×4=1.6A 6+4 6 ×4=2.4A 6+4

在图 b 中 1 A 6 4 ( 1 ) 10 2 ( 1 ) 1 = + i = i = 在图 c 中 4 1.6 A 6 4 ( 2 ) 4 1  = + i = 4 2.4 A 6 4 ( 2 ) 6 2  = + i = ( 1 ) 1 i ( 1 ) 2 i ( 2 ) 1 i ( 2 ) 2 i 图 b 图 c

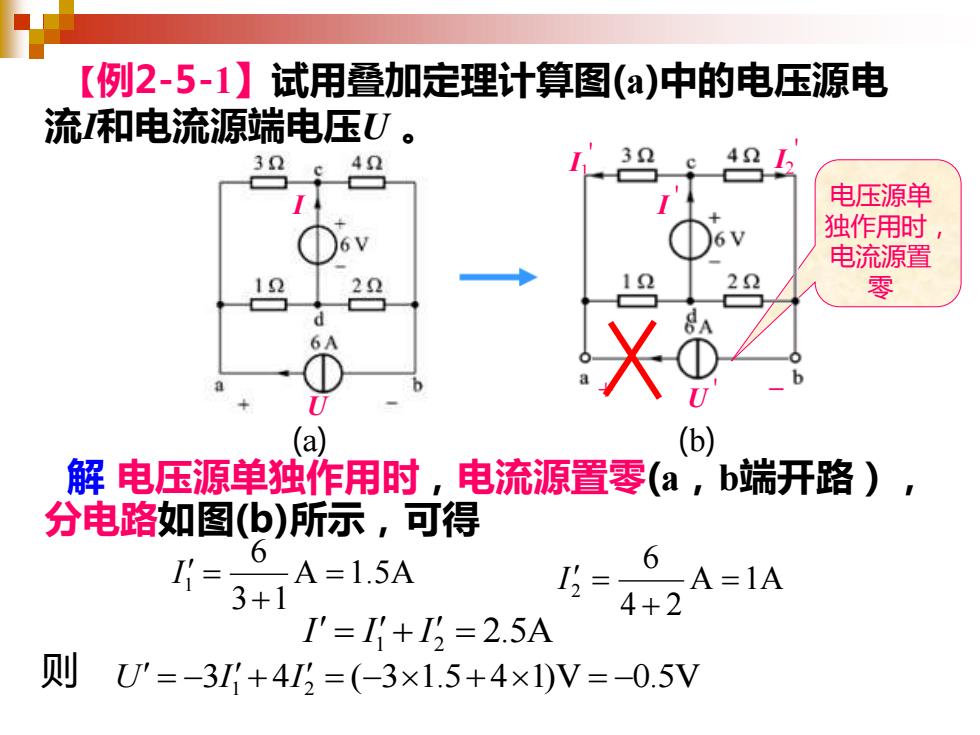
【例2-5-1】试用叠加定理计算图(a)中的电压源电 流和电流源端电压U。 3 4Ω 3 4Ω 电压源单 独作用时， 电流源置 22 1 22 零 (a) (b) 解电压源单独作用时，电流源置零(a,b端开路)， 分电路如图(b)所示，可得 = 0-A=1.5A 6 A=1A 3+1 I3= 4+2 I'=I+I3=2.5A 则U'=-3+4I2=(-3×1.5+4×1)V=-0.5V

【例2-5-1】试用叠加定理计算图(a)中的电压源电 流I和电流源端电压U 。 解 电压源单独作用时，电流源置零(a，b端开路）， 分电路如图(b)所示，可得 (a) (b) U + ' _ U I2 ' I ' I I1 ' A 1.5A 3 1 6 1 = + I = A 1A 4 2 6 2 = + I = U = −3I 1  + 4I 2  = (−31.5+ 41)V = −0.5V I = I 1  + I 2  = 2.5A 则 电压源单 独作用时， 电流源置 零

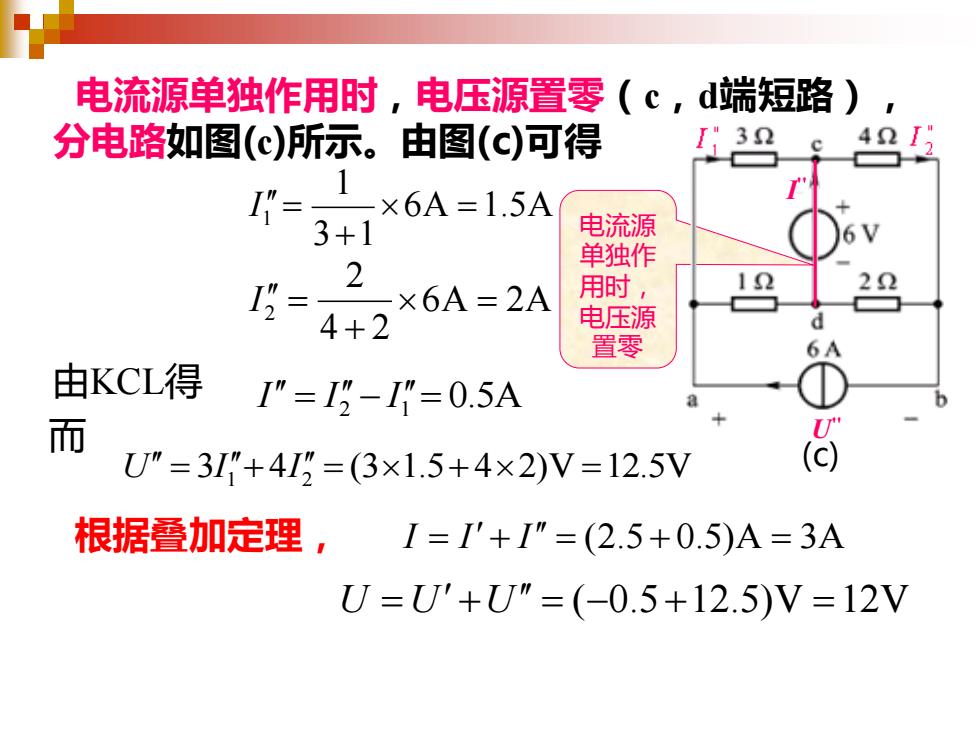
电流源单独作用时，电压源置零（c,d端短路) 分电路如图(c)所示。由图(c)可得 40 1 I'= ×6A=1.5A 3+1 电流源 61 单独作 2 1= ×6A=2A 用时， 22 4+2 电压源 置零 由KCL得 I”=I-I"=0.5A 而 U"=3I"+4I=(3×1.5+4×2)V=12.5V 根据叠加定理，I='+I”=(2.5+0.5)A=3A J=U'+J"=(-0.5+12.5)V=12V

电流源单独作用时，电压源置零（c，d端短路）， 分电路如图(c)所示。由图(c)可得 由KCL得 根据叠加定理， (c) U'' I '' 6A 1.5A 3 1 1 1  = + I = 6A 2A 4 2 2 2  = + I = I = I 2 − I 1  = 0.5A U = 3I 1 + 4I 2  = (31.5+ 42)V =12.5V 而 I = I + I = (2.5+ 0.5)A = 3A U =U +U = (−0.5+12.5)V =12V 电流源 单独作 用时， 电压源 置零

上节内容回顾 叠加原理的内容、验证、解题步骤、几点说明 应用叠加定理求解电路的解题步骤： ()正确画出各独立源单独作用时的分电路。 (2)计算各分电路的响应分量。 (3)叠加各响应分量（代数和）即得原电路中的响应。 几点说明：1.叠加原理只适用于线性电路； 2.对于电压源置零相当于短路； 而对 于电流源置零相当于开路： 3.可以求解电压、电流及电位，功率不能叠加； 4.受控源不能单独作用，应保留不动； 5亦可将独立源分组，按组计算后再叠加

应用叠加定理求解电路的解题步骤： (1)正确画出各独立源单独作用时的分电路。 (2)计算各分电路的响应分量。 (3)叠加各响应分量（代数和）即得原电路中的响应。 上节内容回顾 叠加原理的内容、验证、解题步骤、几点说明 几点说明：1.叠加原理只适用于线性电路； 2. 对于电压源置零相当于短路； 而对 于电流源置零相当于开路； 3.可以求解电压、电流及电位，功率不能叠加； 4.受控源不能单独作用，应保留不动； 5.亦可将独立源分组，按组计算后再叠加