
1 M 将 代 、o=E EI 得到纯弯曲时横截面上正应力的计算公式: M 用册湖 面 细 M为梁横截面上的湾矩, 大道弘 为梁横截面上任意一点到中性轴的距离 L,为梁横截面对中性轴的惯性矩
EIz M = 1 y 将 代入 σ = E 得到纯弯曲时横截面上正应力的计算公式: z I My σ = M为梁横截面上的弯矩; y为梁横截面上任意一点到中性轴的距离; Iz为梁横截面对中性轴的惯性矩

讨论 (1)应用公式时,一般将y以绝对值代入.根据梁变形的情 况直接判断σ的正负号.以中性轴为界,梁变形后凸出边的应 力为拉应力(σ为正号).凹入边的应力为压应力(6为负号); (2)最大正应力发生在横截面上离中性轴最远的点处 Mymax 6max=。 大匠弘玉 引用记号疗 抗弯截面系数 12 max M 则公式改写为 W
讨论 (1)应用公式时,一般将My 以绝对值代入. 根据梁变形的情 况直接判断 的正负号. 以中性轴为界,梁变形后凸出边的应 力为拉应力( 为正号).凹入边的应力为压应力(为负号); (2)最大正应力发生在横截面上离中性轴最远的点处. I M y σ z max max = 则公式改写为 W M σmax = 引用记号 —抗弯截面系数 max y I W z =

(3)当中性轴为对称轴时 实心圆截面W= I 元d4/64L元d3 d/2 d/21 32 所用册线 面翻 矩形截面 b3/12 h/2海纳五/2 大置弘函 空心圆截面W三 πD3 32
( 3 )当中性轴为对称轴时 矩形截面 实心圆截面 空心圆截面 b h z y z dy z Dd y 32 π / 2 π / 64 / 2 4 3 d dd dI W z = = = / 2 6 /12 / 2 3 2 bh h bh hI W z = = = Dd α D W = (1− ) = 32 π 4 3
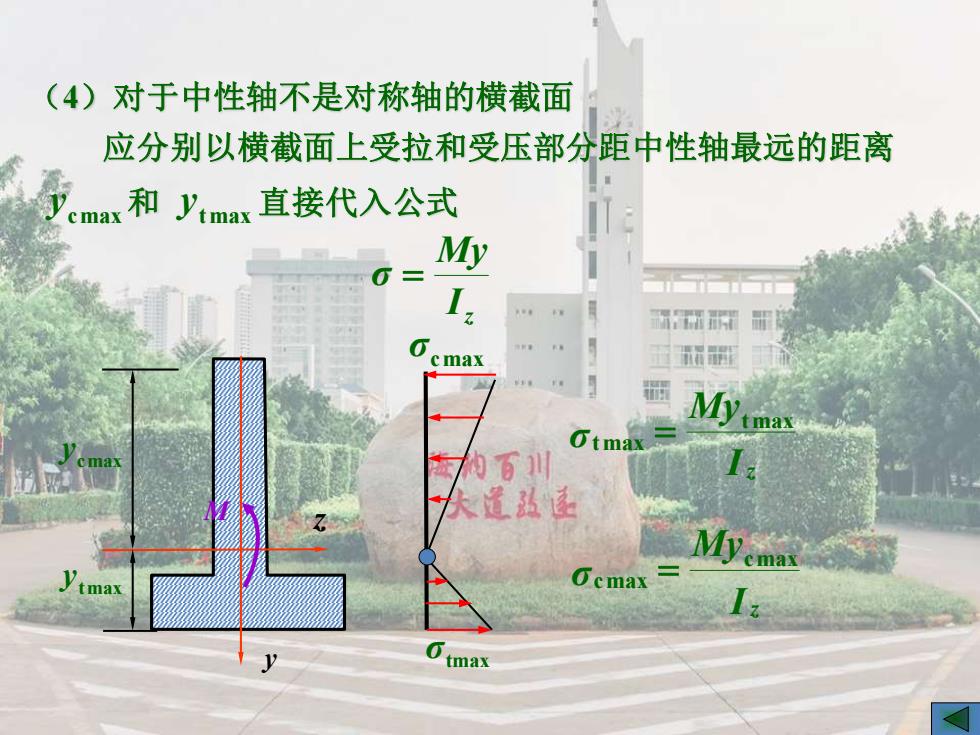
(4)对于中性轴不是对称轴的横截面 应分别以横截面上受拉和受压部分距中性轴最远的距离 cmax和ymax直接代入公式 My I. 霜而 cmax 园 My ma Otmax 为百川 人遥弘函 Ocmax 0tmax
z y (4)对于中性轴不是对称轴的横截面 ycmax ytmax M 应分别以横截面上受拉和受压部分距中性轴最远的距离 ycmax 和 ytmax 直接代入公式 z I My σ = σcmax σtmax I My σ z cmax cmax = I My σ z tmax tmax =

§5-3横力弯曲时的正应力 横力弯曲 当梁上有横向力作用时,横截面上既又弯矩又有剪力.梁在 此种情况下的弯曲称为横力弯曲., 肝际册湖 横力弯曲时,梁的横截面上既有正应力又有切应力切应力 使横截面发生翘曲,横向力引起与中性层平行的纵截面的挤压 应力,纯弯曲时所作的平面假设和单向受力假设都不成立。 虽然横力弯曲与纯弯曲存在这些差异,但进一步的分析表 明,工程中常用的梁,纯弯曲时的正应力计算公式,可以精确的 计算横力弯曲时横截面上的正应力, 等直梁横力弯曲时横截面上的正应力公式为。= M(x) W
当梁上有横向力作用时,横截面上既又弯矩又有剪力.梁在 此种情况下的弯曲称为横力弯曲. §5-3 横力弯曲时的正应力 横力弯曲时,梁的横截面上既有正应力又有切应力.切应力 使横截面发生翘曲,横向力引起与中性层平行的纵截面的挤压 应力,纯弯曲时所作的平面假设和单向受力假设都不成立. 一、横力弯曲 虽然横力弯曲与纯弯曲存在这些差异,但进一步的分析表 明,工程中常用的梁,纯弯曲时的正应力计算公式,可以精确的 计算横力弯曲时横截面上的正应力. 等直梁横力弯曲时横截面上的正应力公式为 W M x σ ( ) =