
2.提出假设 (a)平面假设:变形前为平面的横截面 变形后仍保持为平面且垂直于变形 后的梁轴线; (6)单向受力假设:纵向纤维不相互挤 压,只受单向拉压」 推论:必有一层变形前后长度不变的纤维一中性层 中性轴 中性轴L横截面对称轴 中性层 横截面对称轴
2.提出假设 (a)平面假设:变形前为平面的横截面 变形后仍保持为平面且垂直于变形 后的梁轴线; (b)单向受力假设:纵向纤维不相互挤 压,只受单向拉压. 推论:必有一层变形前后长度不变的纤维—中性层 中性轴 横截面对称轴 中性轴 横截面对称轴 ⊥ 中性层

二、变形几何关系 dx 图(b) 图(c) b_(e+y)de 海物百(p+)d0-pd0 大£益置 bb=dx=00=0'O=pde 应变分布规律: 直梁纯弯曲时纵向纤维的应变与它到中性层的距离成正比
dx 图(b) y z x O 应变分布规律: 直梁纯弯曲时纵向纤维的应变与它到中性层的距离成正比. 图(a) dx 二、变形几何关系 图(c) d z y x O’ O’ b’ b’ y b b O O bb = dx = OO = O'O' = d y y = + − = d ( )d d b b = ( + y)d
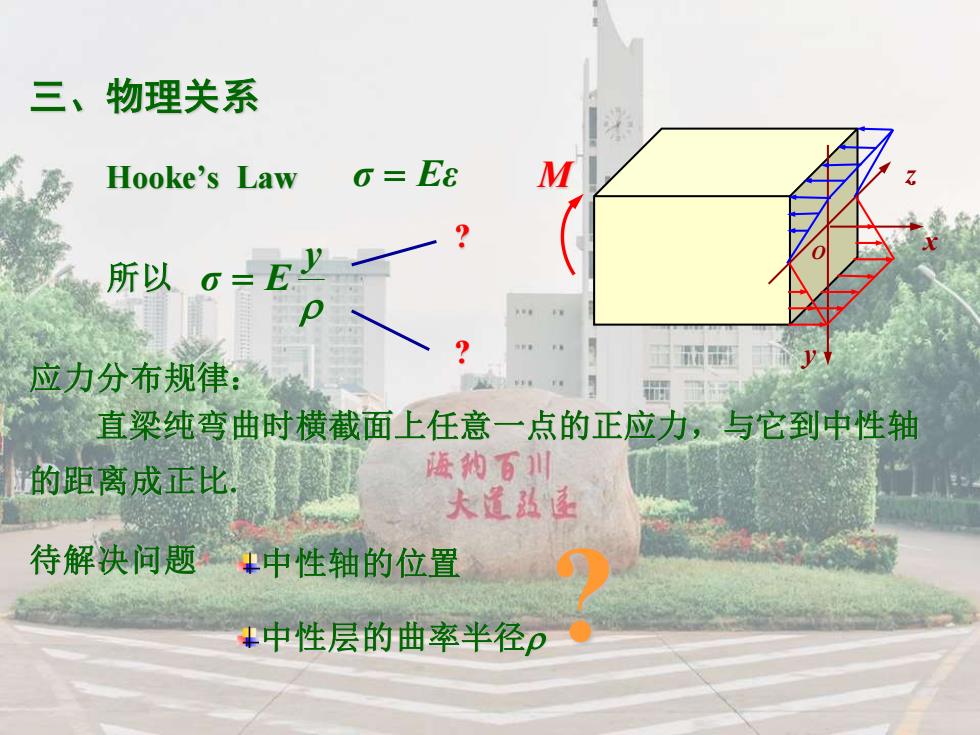
三、物理关系 Hooke's Law o=Ea M 所以=E' 应力分布规律: 翻 直梁纯弯曲时横截面上任意一点的正应力,与它到中性轴 的距离成正比 德纳百川 大置 待解决问题,中性轴的位置 中性层的曲率半径p
三、物理关系 所以 Hooke’s Law M y z O x 直梁纯弯曲时横截面上任意一点的正应力,与它到中性轴 的距离成正比. 应力分布规律: ? 待解决问题 中性轴的位置 中性层的曲率半径 ? ? σ = Eε y σ = E
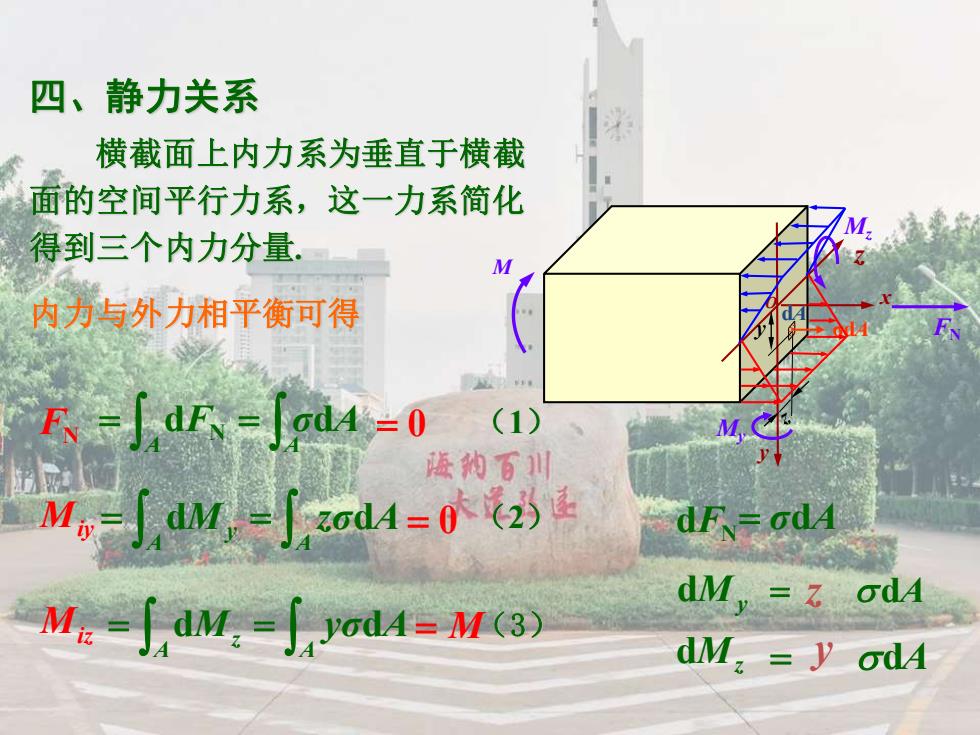
四、静力关系 横截面上内力系为垂直于横截 面的空间平行力系,这一力系简化 得到三个内力分量 内力与外力相平衡可得 F-1 dFv=Jod4 -0 (1) 德纳百川 M,Jo4=024 dF-od4 dM odA M∫dM,=∫od4=M3 dM,=y odA
y z O x M dA y σdA 四、静力关系 横截面上内力系为垂直于横截 面的空间平行力系,这一力系简化 得到三个内力分量. FN Mz My 内力与外力相平衡可得 = d A = d A zy = = A A FN dFN σdA Miy Miz = = A A dMy zσdA = = A A dMz yσdA = 0 (1) = 0 (2) = M (3) dFN dMy dMz= σdA

将应力表达式代入(1)式,得 5-e之4=0→引,4=0÷3-®=0 0 中性轴通过横截面形心 将应力表达式代入(2)式,得 丽霜而 M∫正a4025,d4-0→-2=0 →自然满足川 将应力表达式代入(3)式,得大道弘 M=∫Eyd4=M→ )=M> e1.-M M EI:
将应力表达式代入(1)式,得 将应力表达式代入(2)式,得 将应力表达式代入(3)式,得 中性轴通过横截面形心 z E I M = 1 自然满足 d 0 N = = A y F E A d = 0 A y A E d = 0 A Sz = y A = d = 0 A y M zE A iy d = 0 A yz A E d = 0 A I yz = yz A A M y M yE A iz = = d I M E z = y A M E A = d 2