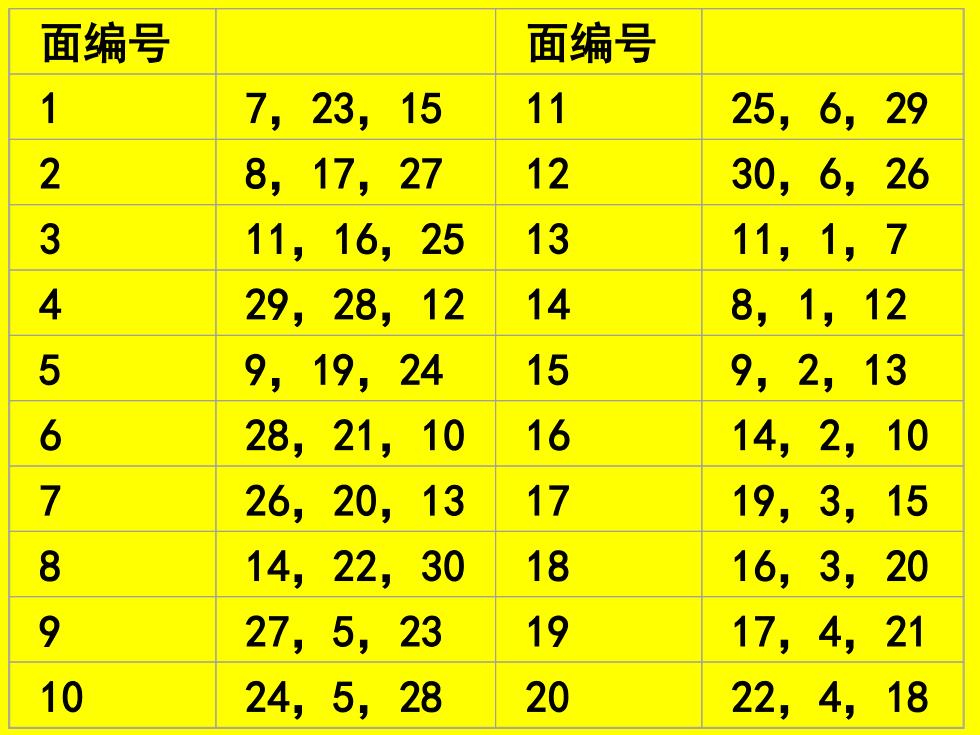
面编号 面编号 1 7,23,15 11 25,6,29 2 8,17,27 12 30,6,26 3 11,16,25 13 11,1,7 4 29,28,12 14 8,1,12 5 9,19,24 15 9,2,13 6 28,21,10 16 14,2,10 7 26,20,13 17 19,3,15 8 14,22,30 18 16,3,20 9 27,5,23 19 17,4,21 10 24,5,28 20 22,4,18
面编号 面编号 1 7,23,15 11 25,6,29 2 8,17,27 12 30,6,26 3 11,16,25 13 11,1,7 4 29,28,12 14 8,1,12 5 9,19,24 15 9,2,13 6 28,21,10 16 14,2,10 7 26,20,13 17 19,3,15 8 14,22,30 18 16,3,20 9 27,5,23 19 17,4,21 10 24,5,28 20 22,4,18

三维实体表示方法 从用户角度来看,形体以特征表示和构 造的实体几何表示比较适宜;从计算机对形 体的存储管理和操作运算角度看,以边界表 示最为实用。 1构造的实体几何法 构造的实体几何(CSG:Constructive Sol id Geometry).法是指任意复杂的形体都 可以用简单形体(体素)的组合来表示。 形体的CSG表示可看成是一棵有序的二 叉树,称为C$G树。其终端结点或是体素, 如长方体、圆锥等;或是刚体运动的变换参 数,如平移参数T等;非终端结点或是正则 的集合运算,一般有交、并、差运算;
• 三维实体表示方法 从用户角度来看,形体以特征表示和构 造的实体几何表示比较适宜;从计算机对形 体的存储管理和操作运算角度看,以边界表 示最为实用。 1 构造的实体几何法 构造的实体几何(CSG:Constructive Solid Geometry)法是指任意复杂的形体都 可以用简单形体(体素)的组合来表示。 形体的CSG表示可看成是一棵有序的二 叉树,称为CSG树。其终端结点或是体素, 如长方体、圆锥等;或是刚体运动的变换参 数,如平移参数Tx等;非终端结点或是正则 的集合运算,一般有交、并、差运算;

或是刚体的几何变换,如平移、旋转等。 采用BNF范式可定义CSG树若下: <CSG>::=<体素叶子><CSG树><正则集合运 算结点><CSG树><CSG树><刚体运动结点><刚 体运动变量> CSG树是无二义性的,但不是唯一的,其定 义域取决于所用体素以及所允许的几何变换 和正则集合运算算子。 CSG表示的优点: 数据结构比较简单,数据量比较小,内部数 据的管理比较容易;
或是刚体的几何变换,如平移、旋转等。 采用BNF范式可定义CSG树若下: <CSG>::=<体素叶子>|<CSG树><正则集合运 算结点><CSG树>|<CSG树><刚体运动结点><刚 体运动变量> CSG树是无二义性的,但不是唯一的,其定 义域取决于所用体素以及所允许的几何变换 和正则集合运算算子。 CSG表示的优点: 数据结构比较简单,数据量比较小,内部数 据的管理比较容易;

每个CSG表示都和一个实际的有效形体所对应; CSG表示可方便地转换成Brep表示,从而可支持 广泛的应用; 比较容易修改CSG表示形体的形状。 CSG表示的缺点: 产生和修改形体的操作种类有限,基于集合运算 对形体的局部操作不易实现; 由于形体的边界几何元素(点、边、面)是隐含 地表示在CSG中,故显示与绘制CSG表示的形体 需要较长的时间
每个CSG表示都和一个实际的有效形体所对应; CSG表示可方便地转换成Brep表示,从而可支持 广泛的应用; 比较容易修改CSG表示形体的形状。 CSG表示的缺点: 产生和修改形体的操作种类有限,基于集合运算 对形体的局部操作不易实现; 由于形体的边界几何元素(点、边、面)是隐含 地表示在CSG中,故显示与绘制CSG表示的形体 需要较长的时间