
基础自主梳理 3.正四边形的作法:用直尺和圆规作圆的两条互相垂直的直 径,就可以把圆4等分,从而作出正四边形.再逐次平分各 边所对的弧,就可以得到正八边形、正十六边形等. 4.正六边形的作法:在圆上作圆的任意一条直径,分别以该直 径两端点为圆心、以圆的半径为半径画弧,则直径的两端点、 弧与圆的交点即为圆的六等分点,从而作出正六边形再平分 所对的弧,就可以作出正十二边形、正二十四边形等同样,把 六等分点中,连接相间的两个点,就可以作出正三角形 导航页
导航页 基础自主梳理 3.正四边形的作法:用直尺和圆规作圆的两条 的直 径,就可以把圆4等分,从而作出正四边形.再逐次 各 边所对的弧,就可以得到正八边形、正十六边形等. 4.正六边形的作法:在圆上作圆的任意一条直径,分别以该直 径两端点为圆心、以 为半径画弧,则直径的两端点、 弧与圆的交点即为圆的六等分点,从而作出正六边形.再_____ 所对的弧,就可以作出正十二边形、正二十四边形等.同样,把 六等分点中,连接 的两个点,就可以作出正三角形. 互相垂直 平分 圆的半径 平分 相间
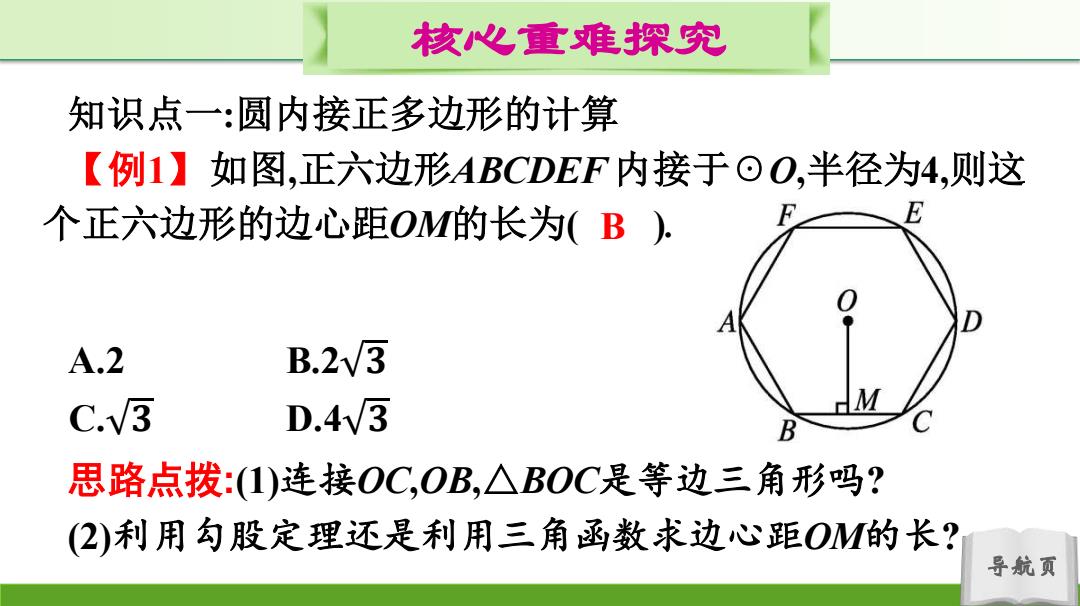
核心心重难探究 知识点一:圆内接正多边形的计算 【例1】如图,正六边形ABCDEF内接于⊙O,半径为4,则这 个正六边形的边心距OM的长为(B), A.2 B.23 C./3 D.4v3 思路点拨:(1)连接OC,OB,△BOC是等边三角形吗? (2)利用勾股定理还是利用三角函数求边心距OM的长? 导航页
导航页 核心重难探究 知识点一:圆内接正多边形的计算 【例1】如图,正六边形ABCDEF 内接于☉O,半径为4,则这 个正六边形的边心距OM的长为( ). A.2 B.2 𝟑 C. 𝟑 D.4 𝟑 思路点拨:(1)连接OC,OB,△BOC是等边三角形吗? (2)利用勾股定理还是利用三角函数求边心距OM的长? B

核心重难探究 【方法归纳】 正多边形的计算,一般是作出正多边形的边心距,连接半径, 把正多边形的边、边心距、外接圆半径以及中心角之间的计 算转化为解直角三角形 导航页
导航页 核心重难探究 【方法归纳】 正多边形的计算,一般是作出正多边形的边心距,连接半径, 把正多边形的边、边心距、外接圆半径以及中心角之间的计 算转化为解直角三角形
核心心重难探究 知识点二:圆内接正多边形的作图 【例2】已知半径为R的⊙O,用多种工具、多种方法作出圆 内接正三角形 思路点拨:)圆内接正三角形的中心角是多少? (2)等边三角形有哪些性质? 导航页
导航页 核心重难探究 知识点二:圆内接正多边形的作图 【例2】已知半径为R的☉O,用多种工具、多种方法作出圆 内接正三角形. 思路点拨:(1)圆内接正三角形的中心角是多少? (2)等边三角形有哪些性质?

核心重难探究 解:方法一:(1)用量角器画圆心角∠AOB (2)连接AB,BC,CA,则△ABC为圆内接1B 方法二:(1)用量角器画圆心角∠AOB=120°; (2)在⊙O上用圆规截取CB=AB; (3)连接AC,BC,AB,则△ABC为圆内接正三角形. 方法三:(1)作直径AD; (2)以D为圆心,以OD长为半径画孤,交回O于B,C; (3)连接AB,BC,CA,则△ABC为圆内接正三角形. 导航页
导航页 核心重难探究 解:方法一:(1)用量角器画圆心角∠AOB=120° ,∠BOC=120° ; (2)连接AB,BC,CA,则△ABC为圆内接正三角形. 方法二:(1)用量角器画圆心角∠AOB=120° ; (2)在☉O 上用圆规截取𝑪 𝑩 = 𝑨 𝑩; (3)连接AC,BC,AB,则△ABC为圆内接正三角形. 方法三:(1)作直径AD; (2)以D为圆心,以OD长为半径画弧,交☉O于B,C; (3)连接AB,BC,CA,则△ABC为圆内接正三角形