
中东理子大 SHANDONG UNIVERSITY OF TECHNOLOGY 反证法 假定>R,则W|>|W 使卡诺热机R逆转成冷冻机, 高温热源 并与热机I联合运行。 吸热22 放热22 这样即可实现从单一热源 做功W 吸热而连续不断做功的第 热21 吸热21 二类永动机,但这是不可 能的。所以<r 低温热源 卡诺定理告诉人们:提高热机效率的有效途径是加 大两个热源之间的温差
17 反证法 低温热源T1 高温热源T2 吸热Q2 放热Q1 做出W 吸热Q2 放热Q1 ’ W’ 假定I > R ,则︳W’ ︳> ︳W ︳ 使卡诺热机R逆转成冷冻机, 并与热机I 联合运行。 吸热Q1 放热Q2 这样即可实现从单一热源 做功W 吸热而连续不断做功的第 二类永动机,但这是不可 能的。所以I < R 卡诺定理告诉人们:提高热机效率的有效途径是加 大两个热源之间的温差。 W

归东理子大名 SHANDONG UNIVERSITY OF TECHNOLOGY Th 高温热源 W=W le' W W W 71三 R= (R一 W Q g'w lo-w 假设 W W T。低温热源 m>n (a) > 18 2025/4/2
18 2025/4/2 18 Th 高温热源 Tc 低温热源 Q1 W Q1 ' W Q1 '−W Q1−W I R (a) W =W I ' 1 W Q = R 1 W Q = 假设 I R > ' 1 1 W Q W Q > 1 1 ' Q > Q
中东翟王大 SHANDONG UNIVERSITY OF TECHNOLOGY Th 高温热源 从低温热源吸热 (2-W)-(Q-W) R =(2-9)>0 o wo-w 高温热源得到热 T低温热源 (2-2) 这违反了Clausiusi说法,只有 (b) 7≤IR 19 2025/4/2
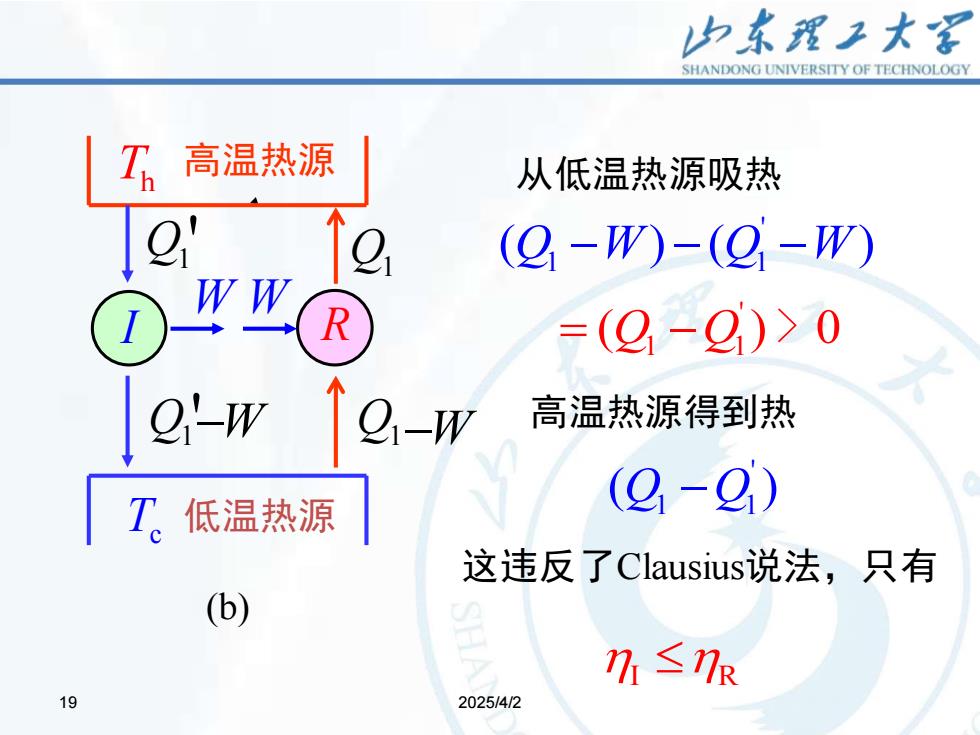
19 2025/4/2 19 Th 高温热源 Tc 低温热源 Q1 W Q1 ' W Q1 '−W Q1−W I R (b) ' 1 1 ( ) ( ) Q W Q W − − − ' 1 1 = − ( ) 0 Q Q > 从低温热源吸热 I R 高温热源得到热 ' 1 1 ( ) Q Q− 这违反了Clausius说法,只有

夕东理工大 卡诺定理→热温商:(Clausius1850年STY OF TEOLY 7R= 2 92 T 1+ =1- T 22 T 号+号=0 卡诺循环(可逆循环)热温商之和等于零 -W_Q2+QT3-T☑ 2 92 0+ 92 ≤0 不可逆循环热温商之和小于零
20 卡诺定理热温商:( Clausius 1850年) 卡诺循环(可逆循环)热温商之和等于零 2 1 2 1 1 1 T T Q Q + = − ⇒ 𝑄1 𝑇1 + 𝑄2 𝑇2 = 0 2 1 2 1 2 2 2 I W Q Q T T Q Q T − + − = = 0 2 2 1 1 + T Q T Q 不可逆循环热温商之和小于零 2 1 2 1 2 2 2 R W Q Q T T Q Q T − + − = = =

§3.4熵的概念 中东理工大 SHANDONG UNIVERSITY OF TECHNOLOGY 从Carnot循环得到的结论: 即Carnot循环中,热效应与温度商值的加和等于零。 2+=0 T1中T2 对于任意的可逆循环,都可以分解为若干个 小Carnot循环。 先以P,Q两点为例 21 2025/4/2
21 2025/4/2 21 §3.4 熵的概念 从Carnot循环得到的结论: 对于任意的可逆循环,都可以分解为若干个 小Carnot循环。 即Carnot循环中,热效应与温度商值的加和等于零。 先以P,Q两点为例 𝑄1 𝑇1 + 𝑄2 𝑇2 = 0