+j Ic=1.690A 100 0.12S3-j0.16S i=1.210°A0s+1 b iI1=253.1°A (c) 图11-5 (e) 并联电容后,图(b)和(©)电路端口的电流变为 i=ij+ic=(ic+I)+Ic=(GUs+YUs)+YcUs =(1.2-j1.6)+j1.6=1.2∠0°A 其相量图如图()所示,由此可见,并联电容后,不会 影响电阻中的电流和吸收的平均功率P-12W。而端口电流 由2A减小到1.2A,提高了电源的利用效率。可以将节省下 来的电流,提供给其它用户使用
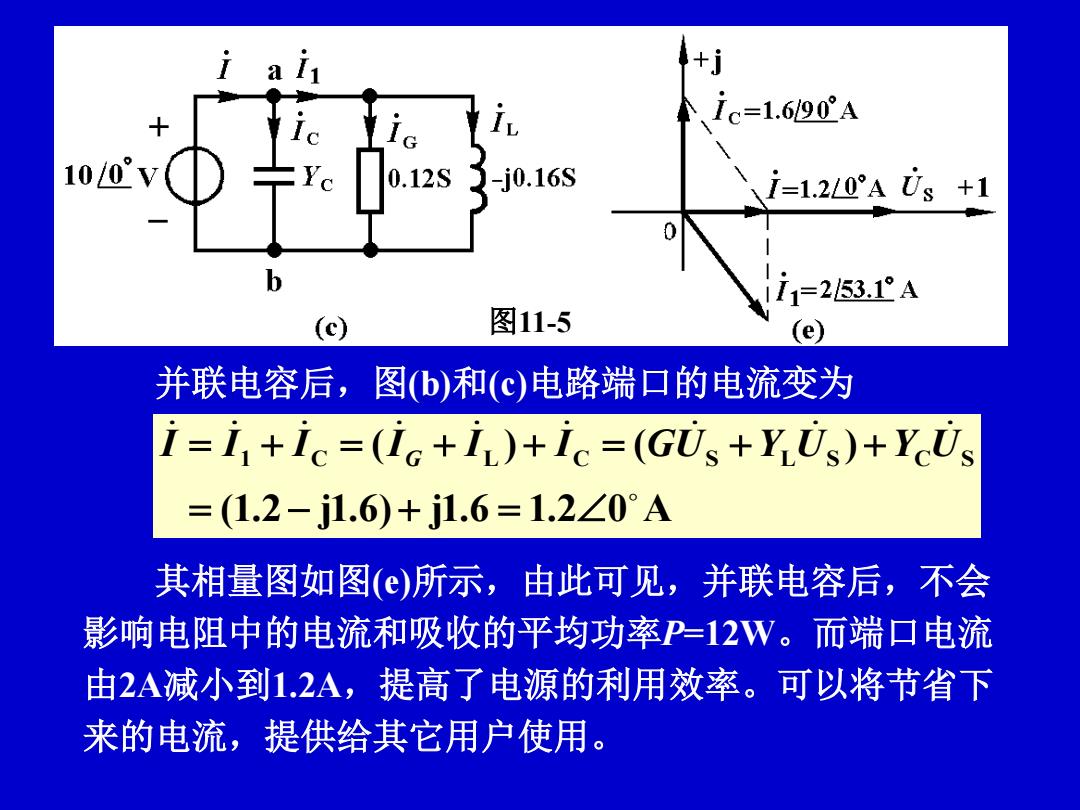
并联电容后,图(b)和(c)电路端口的电流变为 (1.2 j1.6) j1.6 1.2 0 A ( ) ( ) 1 C L C S L S C S I I I I G I I GU Y U Y U 其相量图如图(e)所示,由此可见,并联电容后,不会 影响电阻中的电流和吸收的平均功率P=12W。而端口电流 由2A减小到1.2A,提高了电源的利用效率。可以将节省下 来的电流,提供给其它用户使用。 图11-5
图(a)电路的功率因数2=coso0.6,功率的利用效率很低。 图b)电路并联电容后,功率因数提高到2=cos1。 i ai1 30 32 X 100v 3i4010@ j42 (a) (b) +i 1c=1.690A Us +1 i=1.21四A0s+1 53.1° i=i1=23.1A I1=253.1A (d) (e) 图11-5
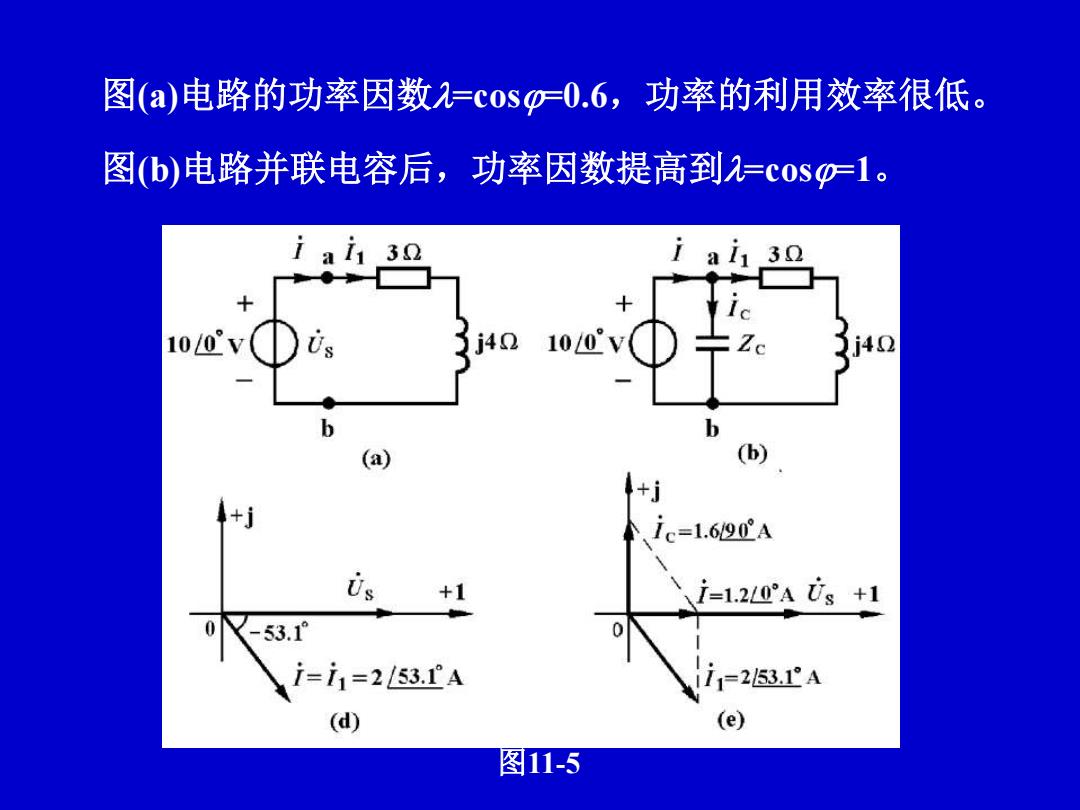
图(a)电路的功率因数=cos=0.6,功率的利用效率很低。 图(b)电路并联电容后,功率因数提高到=cos=1。 图11-5

功率因数的提高 胡翔骏制作 高等教育出版社 幻灯片没有放映时,请用鼠标双击图片放映录像 幻灯片正在放映时,请用鼠标单击图片放映录像
幻灯片没有放映时,请用鼠标双击图片放映录像。 幻灯片正在放映时,请用鼠标单击图片放映录像
§11一2复功率 一、 复功率 为了便于用相量来计算平均功率,引入复功 率的概念。 图11-6所示单口网络工作于正弦稳态,其电压电流 采用关耳 向,假节=ULw. 的有效值 相量分身 N i=I∠W: 图11-6
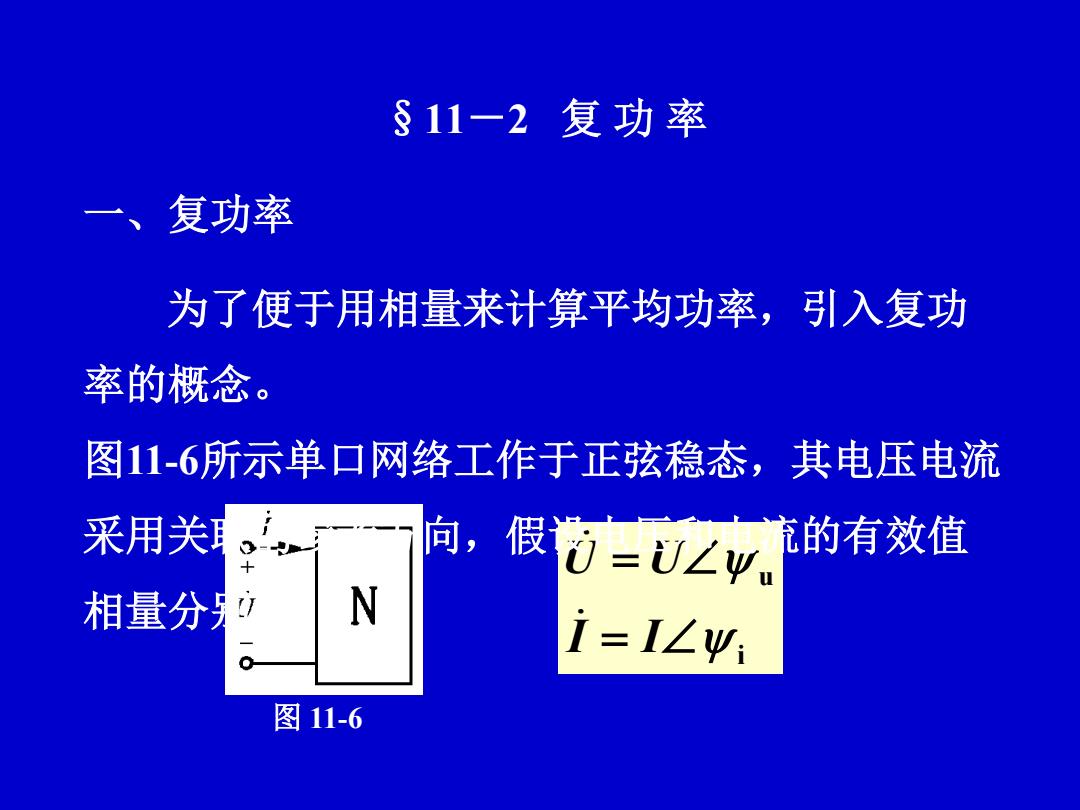
§11-2 复 功 率 一、复功率 图 11-6 i u I I U U 为了便于用相量来计算平均功率,引入复功 率的概念。 图11-6所示单口网络工作于正弦稳态,其电压电流 采用关联的参考方向,假设电压和电流的有效值 相量分别为

N 电流相量的共轭复I=I上Ψ, ,则单口 网络吸收的复功率为 3-0I =UI∠(ym-y)=UI∠p =UI coso+jUlsing=P+jo (11-8) 其中,复功率的实部P=UIcosi称为有功功率, 它是单口网络吸收的平均功率,单位为瓦(W)
电流相量的共轭复数为 ,则单口 网络吸收的复功率为 ψ i I I * cos (11 8) ( ) ~ * U I U I P Q U I U I S U I u j sin j 其中,复功率的实部P=UIcos称为有功功率, 它是单口网络吸收的平均功率,单位为瓦(W)