
5、3dB带宽 当0=0时,(Q)-2,920.707 201og,(j.)=-3dB,即相当于3dB衰减
5、3dB带宽 20logH (jΩ ) 3dB,即相当于3dB衰减 0.707 2 1 或H (jΩ ) 2 1 当 Ω Ω 时,A(Ω) a c a c 2 c = − = = = =

6、Butterworth滤波器的特点 *(1)N阶滤波器在Ω=0处幅度平方函数的前(N-1)阶导 数等于零。即(Q)=H(2在Ω=0处,最平坦,且随 着Ω的增加单调下降。 *(2)在止带内的逼近是单调变化的,不管N为多少, 所有H,()都经过2点(-3B)处。 *(3)滤波器的特性完全由其阶数N决定。N越大,则通 带内在更大范围内更接近于1,在止带内迅速地接近 于零,因而振幅特性更接近于理想的矩形频率特性
(1)N阶滤波器在Ω=0处幅度平方函数的前(N-1)阶导 数等于零。即 在Ω=0处,最平坦,且随 着Ω的增加单调下降。 (2)在止带内的逼近是单调变化的,不管N为多少, 所有 都经过 点(-3dB)处。 (3)滤波器的特性完全由其阶数N决定。N越大,则通 带内在更大范围内更接近于1,在止带内迅速地接近 于零,因而振幅特性更接近于理想的矩形频率特性。 6、Butterworth滤波器的特点 2 2 A () = H (j) a H (j) a 2 1

7、归一化的Butterworth滤波器 的系统函数 *在一般设计中,都先把Qc设为1rad/s,这样使频率得 到归一化。归一化的Butterworth滤波器的极点分布以 及相应系数都有现成表可查即若令 5= S 2. 1 H,=1.(-0.=1+a5+a,52++a-5+5
在一般设计中,都先把Ωc 设为1rad/s,这样使频率得 到归一化。归一化的Butterworth滤波器的极点分布以 及相应系数都有现成表可查即若令 7、归一化的Butterworth滤波器 的系统函数 N N N a a s s c a s a s a s s H s H s s s c + + + + + = = = − − = 1 1 2 1 2 1 1 ( ) ( )
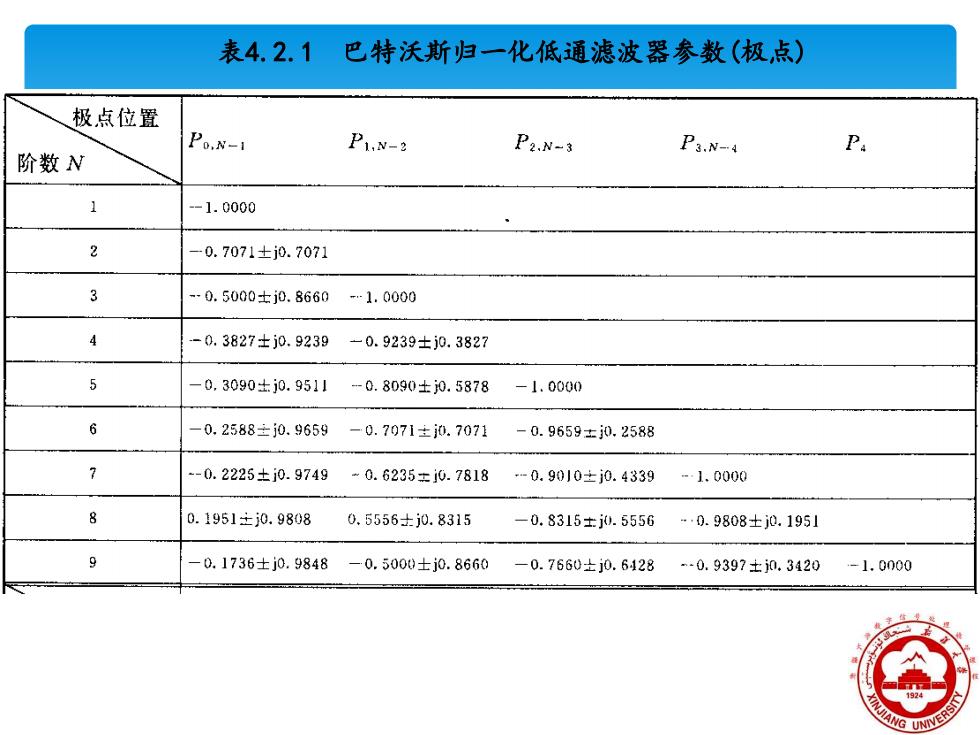
表4,2.1巴特沃斯归一化低通滤波器参数(极,点) 极点位置 P0.N-1 P1,N-2 P2.N-3 P3.N-4 P. 阶数N -1.0000 2 -0.7071±j0.7071 3 -0.5000士j0.8660 -.1.0000 -0.3827士j0.9239 -0.9239±j0.3827 5 -0,3090±j0.9511 -0.8090±j0.5878 -1.0000 6 0,2588壬j0.9659 -0.7071±0.7071 -0.9659±0.2588 -0.2225±j0.9749 w0.6235=j0.7818 -0.9010±j0.4339 -1.0000 0.1951±j0.9808 0.5556±j0.8315 -0.8315士.j.5556 .0.9808±j0.1951 9 0.1736±j0.9848 -0.5000士j0.8660-0.7660±j0.6428-0.9397±j0.3420-1.0000
表4.2.1 巴特沃斯归一化低通滤波器参数(极点)

表4.2.2巴特沃斯归一化低通滤波器参数(分母多项式) 分母多项式B(p)=pN+bx-1p-l+hw2pv-2+.十bp+h 系数阶数N b2 b3 bs 1 1.0000 2 1.0000 1.4142 3 1.0000 2.0000 2.0000 1.00002.6131 3.41422.613 5 1.00003.2361 5.2361 5.23613.2361 6 1.00003.8637 7.4641 9.14167.4641 3.8637 7 1.0000 4.4940 10.097814.5918 14.591810.09784.4940 8 1.0000 5.1258 13.137121.8462 25.688421.864213.13715.1258 9 1.00005.7588 16.58173L.163441.986441.986431.163416.58175.7588 归一化低通滤波器的系统函数原型为: Ha(p)= B(D) 实际的滤波器传输函数Ha(s): Ha(s)=Ha(p)l
( ) 1 Ha( ) B p p = 归一化低通滤波器的系统函数原型为: c s p Ha s Ha p = 实际的滤波器传输函数 ( ) = ( )| Ha(s): 表4.2.2 巴特沃斯归一化低通滤波器参数(分母多项式)