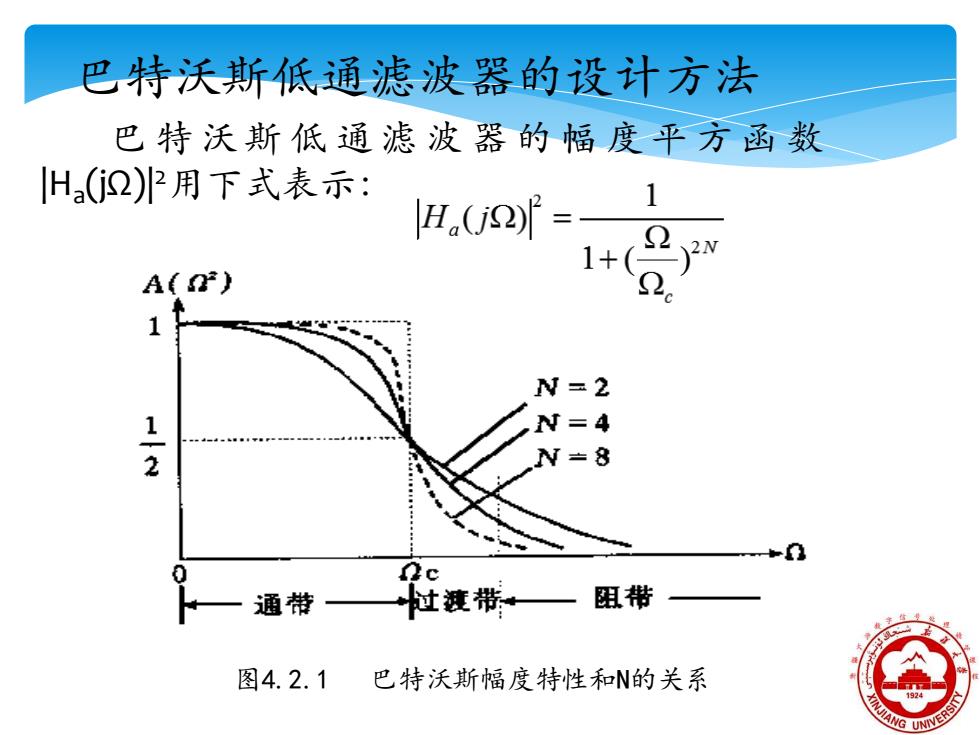
巴特沃斯低通滤波器的设计方法 巴特沃斯低通滤波器的幅度平方函数 H(2)2用下式表示: H,(j2= 1+0 Af N=2 1-2 N=4 N=8 c 通带 过液带一 阻带 图4.2.1 巴特沃斯幅度特性和N的关系
巴特沃斯低通滤波器的设计方法 巴 特 沃 斯 低 通 滤 波 器 的 幅 度 平 方 函 数 |Ha (jΩ)|2用下式表示: 图4.2.1 巴特沃斯幅度特性和N的关系

2、 Butterworth滤波器的极点分布 由 H,2 2 可知Butterworth的零,点全部在S=o处,它是全极点型滤 波器,且分布在半径为2〔的圆上,呈象限对称分布。 *为了得到稳定的滤波器,S左半平面的极,点必须分配给 Ha(s),s右半平面的极,点分配给Ha(-s)。 即:H(s)H(←s)=1 -,令分母=0,得 1+(S)2 1 +2k-1 sk=(-1)2w(2)=2.e9+2w,k=1,2.,2W 米」 取其分布在左平面的极点, 设计出巴特沃斯低通滤波器
由 可知Butterworth的零点全部在S=∞处,它是全极点型滤 波器,且分布在半径为Ωc 的圆上,呈象限对称分布。 为了得到稳定的滤波器,s左半平面的极点必须分配给 Ha(s),s右半平面的极点分配给Ha(-s)。 取其分布在左平面的极点, 设计出巴特沃斯低通滤波器. 2、Butterworth滤波器的极点分布 N c H a j 2 1 ( ) 1 ( ) + = s j e k N j s H s H s N k j c c N k N c a a ( 1) ( ) , 1,2 ,2 ,令分母 0,得 1 ( ) 1 即: ( ) ( ) ] 2 2 1 2 1 [ 2 1 2 = − = = = + − = − +
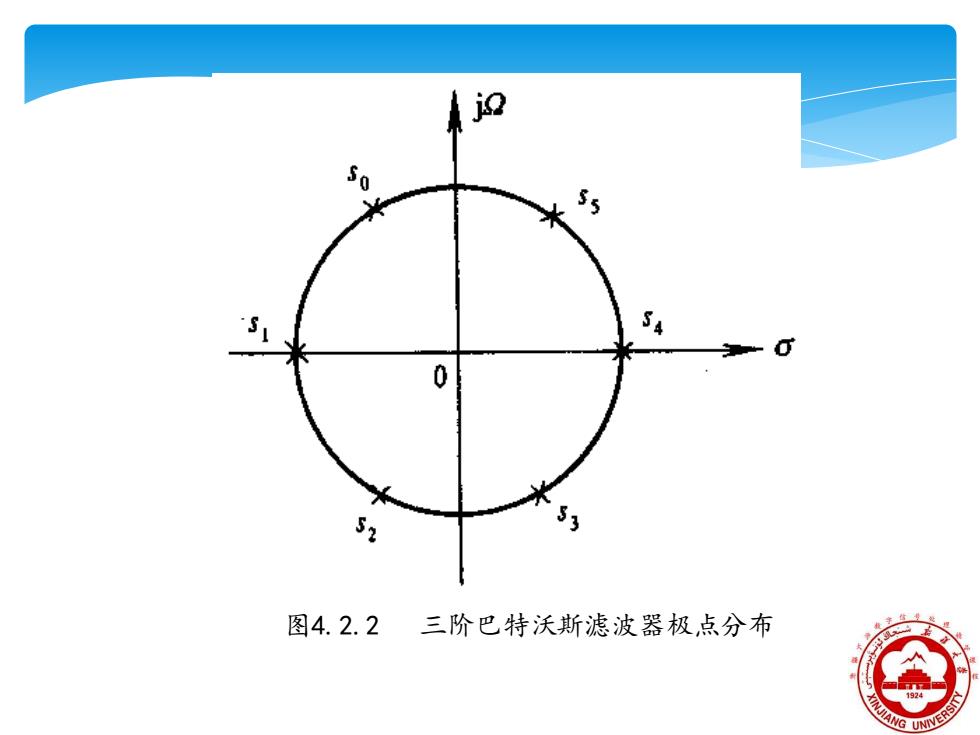
59 55 54 0 52 图4.2.2三阶巴特沃斯滤波器极点分布
图4.2.2 三阶巴特沃斯滤波器极点分布
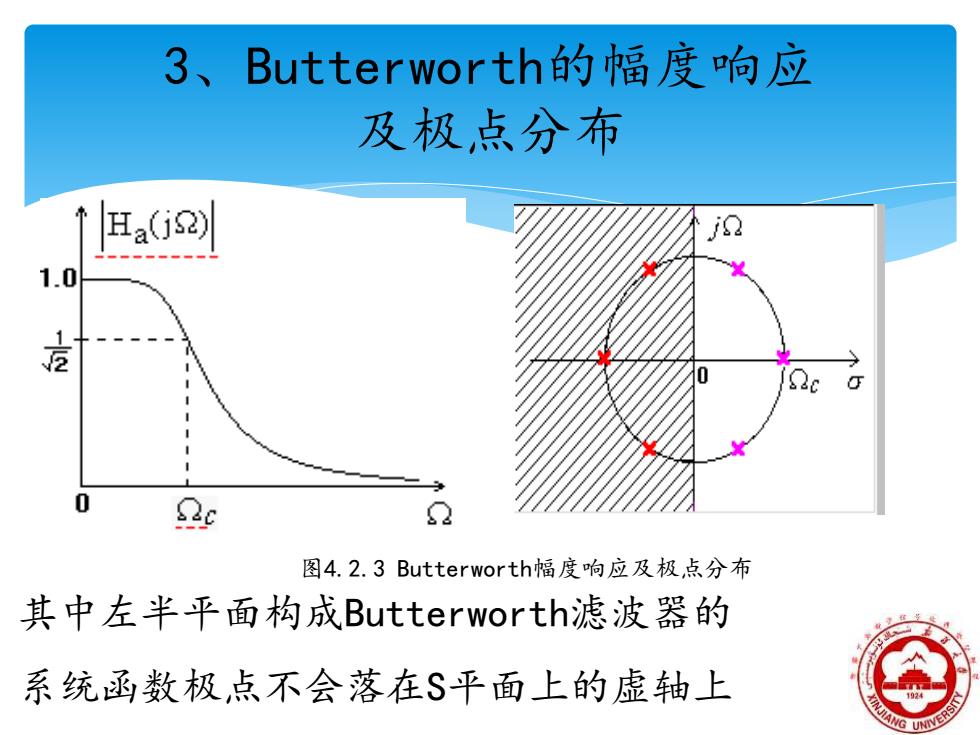
3、Butterworth的幅度响应 及极,点分布 Ha(j2) 1.0 克 0 Qc 图4.2.3 Butterworth幅度响应及极,点分布 其中左半平面构成Butterworth滤波器的 系统函数极点不会落在S平面上的虚轴上
3、Butterworth的幅度响应 及极点分布 其中左半平面构成Butterworth滤波器的 系统函数极点不会落在S平面上的虚轴上 图4.2.3 Butterworth幅度响应及极点分布
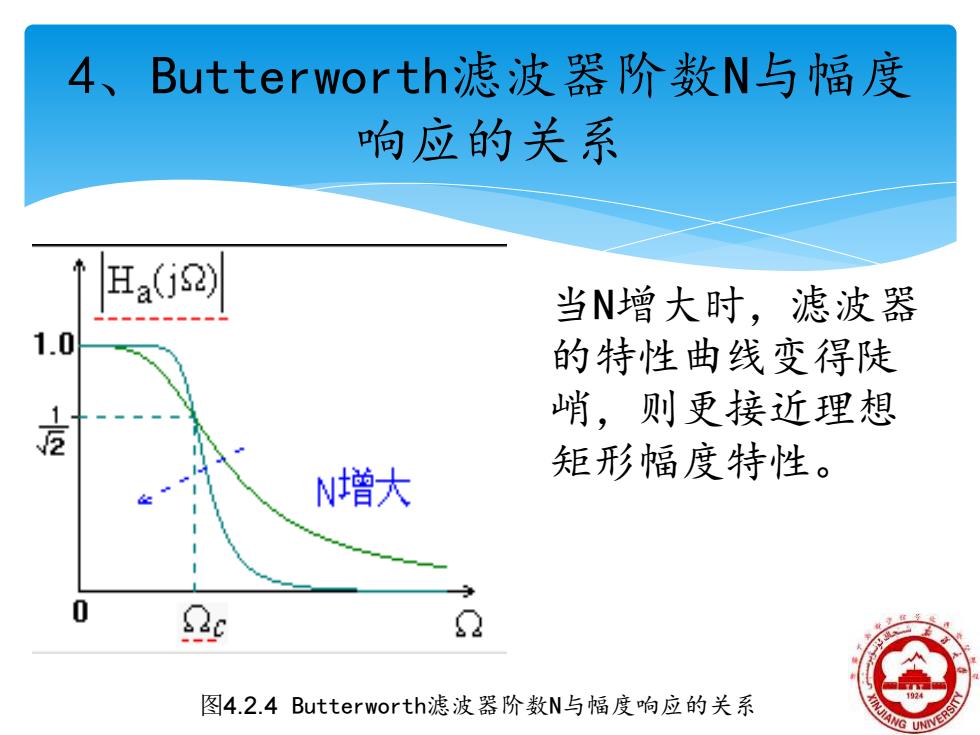
4、Butterworth滤波器阶数N与幅度 响应的关系 Ha(j22) 当N增大时,滤波器 1.0 的特性曲线变得陡 峭,则更接近理想 N增大 矩形幅度特性。 Qo 8 图4.2.4 Butterworth:滤波器阶数N与幅度响应的关系
4、Butterworth滤波器阶数N与幅度 响应的关系 当N增大时,滤波器 的特性曲线变得陡 峭,则更接近理想 矩形幅度特性。 图4.2.4 Butterworth滤波器阶数N与幅度响应的关系