
2.2热传导 傅立叶定律 高温 七2 n t q=-λ On 低温 t=f(x,y,z,t) 等温面 dt 维稳态导热 9=- dx
2.2 热传导 一、 一维稳态导热 dx dt q = −

2.2热传导 ■二、基本概念 ·Fourier'sLaw:与牛顿粘性定律类似 ·导热系数 ■物理意义一物质导热能力的大小 ■ 影响因素 ■导热系数随温度的变化 ·物质导热系数数量级?
2.2 热传导 二、基本概念 Fourier’s Law:与牛顿粘性定律类似 导热系数 物理意义——物质导热能力的大小 影响因素 导热系数随温度的变化 物质导热系数数量级?

导热系数 20℃时的 a值[Wf-K] 压力南 迅底响 典型实例 气体 0.0080.8 空气0.025 不太大 融塘证度的升高,k信增大 液体 0.090.7 本0,504 」儿乎不受影将 健鳍祖度的升高,1值变小 水是一种例外,大的在120℃ 时汰到最大值,超过此退度时 值又变小 固体 相当大 铜312 几子不受形响: 随粉温度的升高,入值变小
导热系数
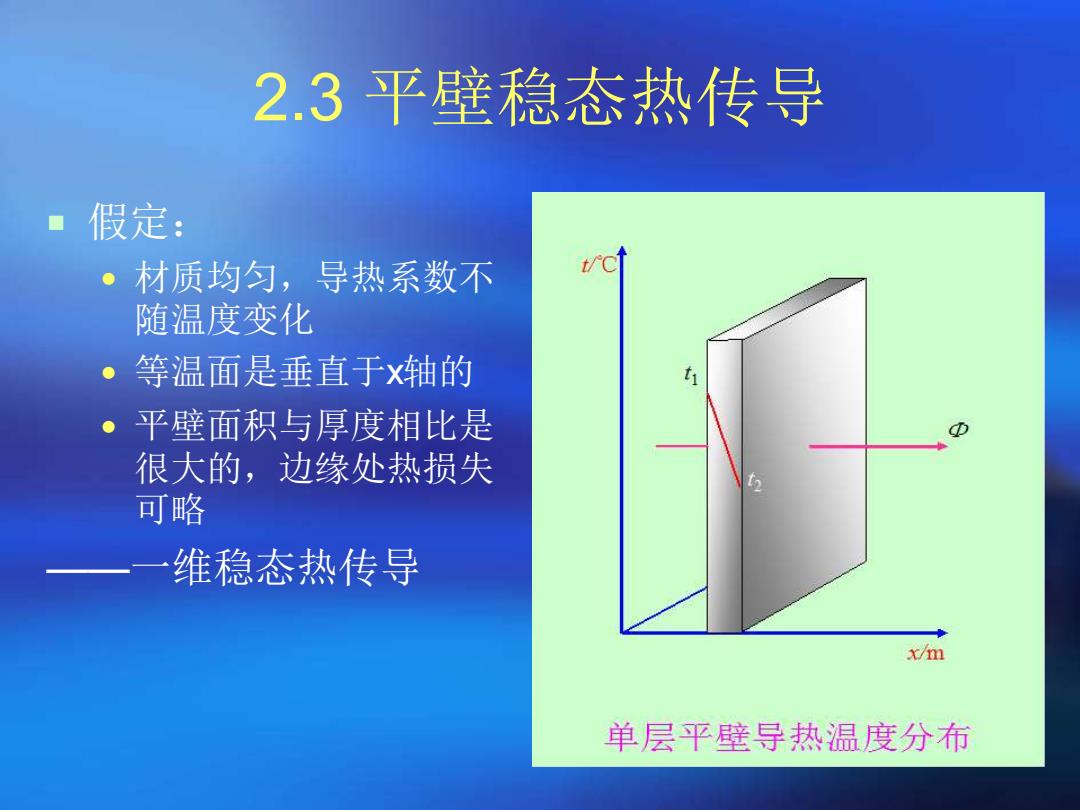
2.3平壁稳态热传导 假定: ·材质均匀,导热系数不 随温度变化 等温面是垂直于x轴的 平壁面积与厚度相比是 很大的,边缘处热损失 可略 维稳态热传导 x/m 单层平壁导热温度分布
2.3 平壁稳态热传导 假定: 材质均匀,导热系数不 随温度变化 等温面是垂直于x轴的 平壁面积与厚度相比是 很大的,边缘处热损失 可略 ——一维稳态热传导

一维单层平壁稳态导热 9= =-元 dA ■单层平壁 x=0,t=t2 。x=o,t=t, 0=元AG2-)/6 考虑入随温度的变化,入取平均值
t dx dt dA dQ q = = − = Q = A(t 2 −t 1 )/ 一维单层平壁稳态导热 单层平壁 x=0, t=t2 x=σ, t=t1 考虑随温度的变化, 取平均值