《电路》课程教学资源（PPT课件）第九章 正弦稳态电路的分析

电路正稳态电路的分折相量图1注意U,=8.42>U=5，3分电压大于总电压返上回页页

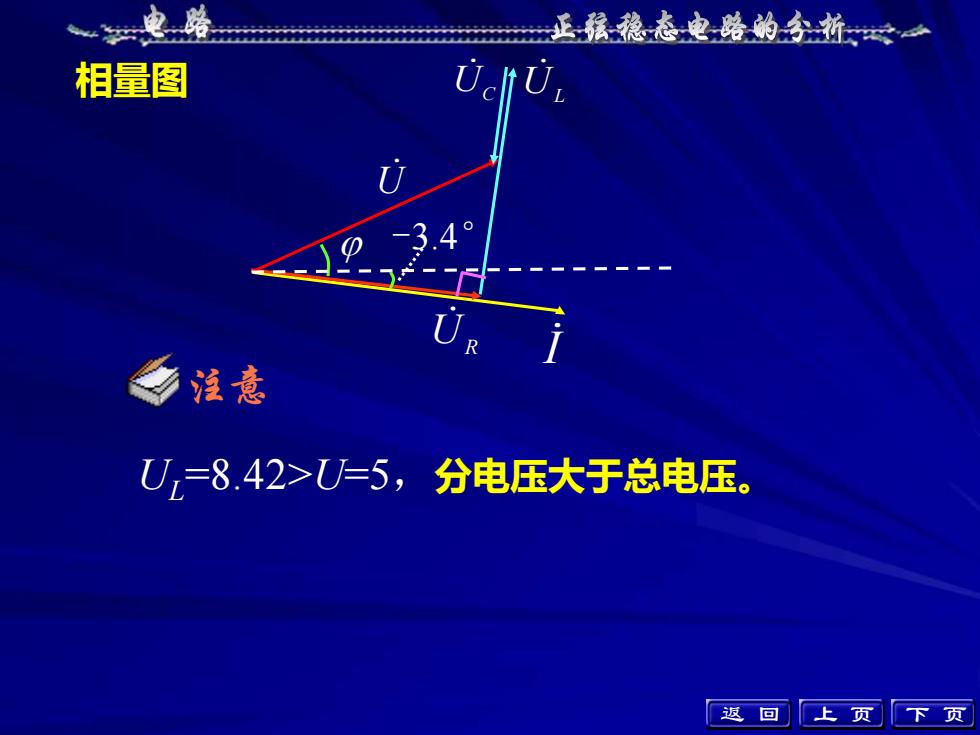
上 页 下 页 UL=8.42>U=5，分电压大于总电压。 相量图 注意 U  UL  UC  I UR    -3.4° 返 回

电路正弦稳态电路的分析3.导纳正弦稳态情况下无源线性网络定义导纳==YI, SY(Y\=导纳模导纳角,=V,-VD返上回页N

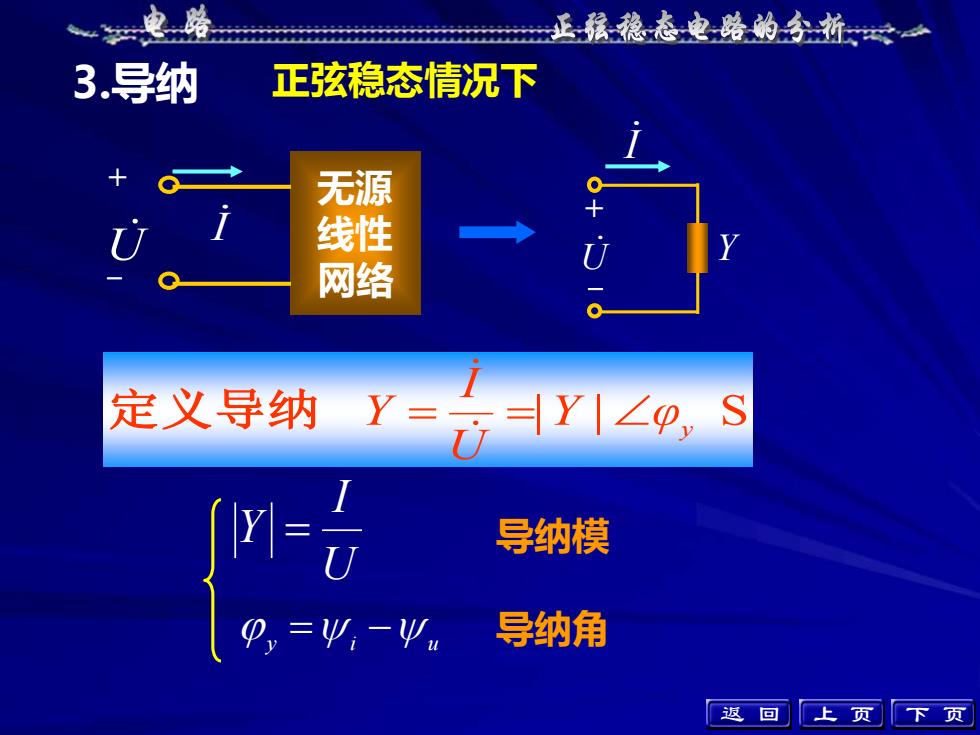
3.导纳 正弦稳态情况下 |Y | φy S U I Y = =    定义导纳 y = i − u U I Y = 导纳模 导纳角 上 页 下 页 无源 线性 网络 I  U  + - I  U  Y + - 返 回

电路正弦稳态电路的分析山1对同一二端网络：.Y:Z=二 Z当无源网络内为单个元件时有：二iR=joC= jBcJBRjo L表明Y可以是实数，也可以是虚数。返上回页N

Z Y Y Z 1 , 1 对同一二端网络: = = 当无源网络内为单个元件时有： G U R I Y = = = 1   BL U L I Y j j 1 = = =    BC C U I Y j j = = =    Y 可以是实数，也可以是虚数。 上 页 下 页 I  C U  + - I  U  R + - I  L U  + - 表明 返 回

电路稳态电路的分析山正4.RLC并联电路uRRjQL0由KCL: i=ir+it+ic=GU-j-U+ joCUQL(G-j+ joC)U=[G+ j(B, + B.)U =(G+jB)UQL=G+ jB=Xβ=G+ joC-j=πOL返回上页

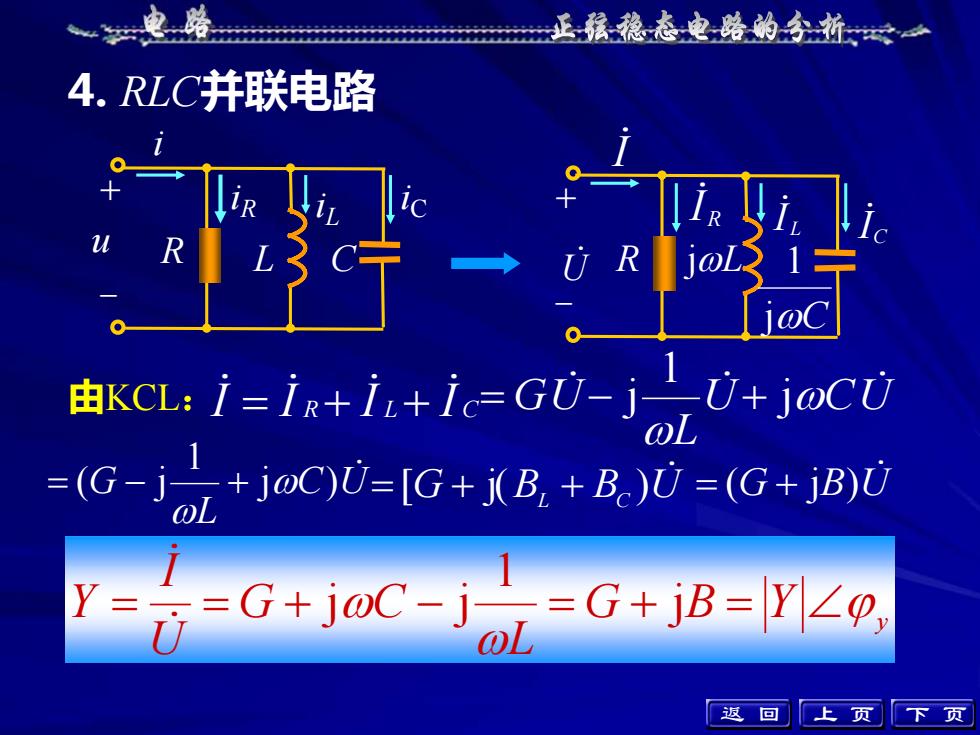
4. RLC并联电路 由KCL： I I R I L I C  =  +  +  j 1 j U CU L GU     = − + j ) 1 ( j C U L G    = − + =[G + j(BL + BC )U = (G + jB)U G B Y y L G C U I Y   = = +  − = + j =  1 j j   上 页 下 页 i R L C u iL iC + - iR R + - I  U  jL IL  I C  jC 1 IR  返 回

#电路正弦稳态电路的分析导纳角；Y一复导纳；IYI一复导纳的模；G一电导(导纳的实部)；B一电纳(导纳的虚部);IY|= √G? + B转换关系：B= arctanDG[)=G=|Y]cos y或B-|Y|sinP ,P, =, -V,YB导纳三角形0返上回页下页

Y—复导纳；|Y| —复导纳的模；y—导纳角； G —电导(导纳的实部)；B —电纳(导纳的虚部)； 转换关系： arctan | | 2 2      = = + G B φ Y G B y 或 G=|Y|cos y B=|Y|sin y 导纳三角形 |Y| G B  y y i u U I Y  = − = 返 回 上 页 下 页