
二、列体体系虚功原理的两种应用 对于具有理想约束的刚体体系,其虚功 原理为:设体系上作用任意的平衡力系 又设体系发生符合约束条件的无限小刚体 体系位移,则主动力在位移上所作的虚功 总和恒等于零。 即: W.=0 (9-2) 理想约束一 约束力在可能位移上所作的功恒 等于零的约束,如:光滑铰链、刚性链杆等。 刚体 具有理想约束的质点系。刚体内力 在刚体的可能位移上所作的功恒为零
二、刚体体系虚功原理的两种应用 • 对于具有理想约束的刚体体系,其虚功 原理为:设体系上作用任意的平衡力系, 又设体系发生符合约束条件的无限小刚体 体系位移,则主动力在位移上所作的虚功 总和恒等于零。 • 即: W e = 0 • 理想约束——约束力在可能位移上所作的功恒 等于零的约束,如:光滑铰链、刚性链杆等。 • 刚体 ——具有理想约束的质点系。刚体内力 在刚体的可能位移上所作的功恒为零。 (9-2)

虚功原理(又称虚位移原理、虚力原理 用于讨论静力学问题非常方便,是分析力学的 基础。 因为虚功原理中平衡力系与可能位移无关 所以既可把位移视为虚设的,也可把力系视为 虚设的。 根据虚设的对象不同,虚功原理有两种应 用形式,解决两类不同的问题。 虚功原理的两种不同应用,不但适用于刚 体体系,也适用于变形体体系
• 虚功原理(又称虚位移原理、虚力原理) 用于讨论静力学问题非常方便,是分析力学的 基础。 • 因为虚功原理中平衡力系与可能位移无关, 所以既可把位移视为虚设的,也可把力系视为 虚设的。 • 根据虚设的对象不同,虚功原理有两种应 用形式,解决两类不同的问题。 • 虚功原理的两种不同应用,不但适用于刚 体体系,也适用于变形体体系

1、求静定结构的未知约束力 应用虚功原理计算静定结构某一约束力X(包括 支座反力或任一截面的内力)步骤如下: (1)撤除与X相应的约束,代以相应的约束力X, 使原来的静定结构变为具有一个自由度的机构,约 束力X变成主动力X,X与原来的力系维持平衡。 (2)令机构发生一刚体体系的可能位移,沿X正 方向相应的位移为单位位移,即δ=1,这时,与荷 载P相应的位移为δ,得到一个虚位移状态
1、求静定结构的未知约束力 应用虚功原理计算静定结构某一约束力X(包括 支座反力或任一截面的内力)步骤如下: (1)撤除与X相应的约束,代以相应的约束力X, 使原来的静定结构变为具有一个自由度的机构,约 束力X变成主动力X,X与原来的力系维持平衡。 (2)令机构发生一刚体体系的可能位移,沿X正 方向相应的位移为单位位移,即δx=1,这时,与荷 载P相应的位移为δp,得到一个虚位移状态

(3)在平衡力系和虚位移之间建立虚功方程 X1+2Pδ,=0 (4)求出单位位移6=1与6之间的集合关系,代 入虚功方程,得到 X=-Pδp 这种求约束力和内力的方法,称单位位移法。见教 材P137例9.1
(3)在平衡力系和虚位移之间建立虚功方程 X·1+ΣP δp=0 (4)求出单位位移δx=1与δp之间的集合关系,代 入虚功方程,得到 X=-ΣP δp 这种求约束力和内力的方法,称单位位移法。见教 材P137例9.1
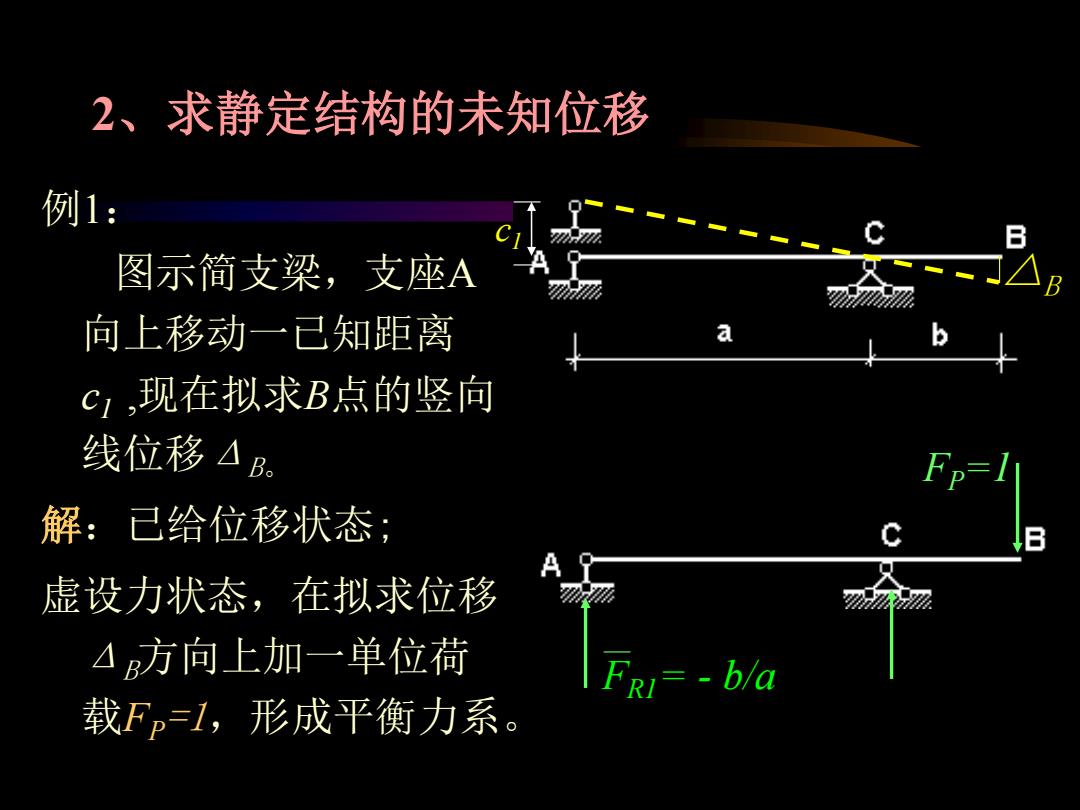
2、求静定结构的未知位移 例1: 图示简支梁,支座A 向上移动一已知距离 a C,,现在拟求B点的竖向 线位移△B. 解:已给位移状态; 虚设力状态,在拟求位移 △方向上加一单位荷 =-b/a 载Fp1,形成平衡力系
2、求静定结构的未知位移 例1: 图示简支梁,支座A 向上移动一已知距离 c1 ,现在拟求B点的竖向 线位移ΔB。 解:已给位移状态; 虚设力状态,在拟求位移 ΔB方向上加一单位荷 载FP=1,形成平衡力系。 c1 △B FP=1 FR1= - b/a